明渠均匀流的断面平均流速优化

明渠恒定均匀流动中，如果过水断面的形状、底坡、流量都沿程不变，则水深和流速将完全取决于边壁的粗糙程度、阻力大小。光滑边壁情况下，水深小，流速高。边壁越粗糙，水流阻力越大，流速越慢，水深越大。经验或半经验性的断面平均流速公式，给出了流速与阻力系数或边壁粗糙程度的定量关系，同时也给出了把边壁粗糙程度表达为阻力系数的方法。不同的断面平均流速公式提供的定量关系和表达方法是不同的，但可通过一定的方法互相换算。

（一）常用的断面平均流速公式

对于阻力平方区的明渠紊流，工程中常用的断面平均流速公式主要有：

（1）Chezy公式（Chezy′s formula）。这一著名公式形式为

式中：U为断面平均流速（m/s）；C为Chezy系数；R和J分别为水力半径（R=A/P，m）和水力坡降（无量纲）。

为满足量纲和谐，C的单位取为（m1/2/s）。式中单位为公制，长度单位必须是米。法国工程师AntoinêChézy于1769年间，在Courpalet运河和Seine河上进行了试验和观测，用所获资料建立并验证了该式，随着不断应用而逐渐推广。Chezy系数C既与床面糙率有关，又与水深有关（床面糙率相同、水深不同时，C的值也不同）。对于充分发展的明渠紊流，可通过Manning公式来计算Chezy系数C。

（2）Manning公式（Manning′s formula）。爱尔兰工程师Robert Manning依据Darcy和Bazin于1865年发表的明渠水流试验资料，于1889年提出了Manning公式的最初形式，后改写为如下的国际单位制形式（m-kg-s制）

和英制单位形式

式中：n是Manning系数，也称为粗糙系数，通常称为糙率。

由于在该公式的两种单位制形式中，n的数值不受影响，所以它在两种单位制体系中都得到了广泛的应用。在国际单位制形式（m-kg-s制）中，为满足量纲和谐，n的单位取（s·m—1/3）。此式简单易用，为工程界广泛采用。对比式（3-36）和式（3-37），得到

这就是Chezy系数C和Manning系数n的关系。天然河流中的流动一般都处于紊流的阻力平方区，如果流动可视为二维的（如宽浅河流），或河岸、河底具有相同的糙率，则n与水深无关。但n常常与水流状态有关，这很大程度上是天然河流河底、河岸边界的可变性造成的。如河底沙波的消长，或当河渠中有杂草生长时，水流强度低的情况下杂草直立使n值较大，而水流强度大的情况下（例如发生洪水时），杂草会倒伏，使得n值较小。

（3）Darcy-Weisbach公式。它原是在管道流动的研究中建立的。Julius Weisbach在1845年出版的教科书《工程力学》中提出了这一公式，其后Darcy于1854年又对该式作了进一步的试验研究和完善。由Bernoulli能量方程可以推导出管道流动的沿程水头损失hf为

式中：L为管道长度；d0为管道内直径。一些教科书中常用符号λ代替f。因为能坡J=hf/L，由上式可得到Darcy-Weisbach断面平均流速公式为

式中：f为Darcy-Weisbach摩阻系数（无量纲）；U为断面平均流速；ρ为流体密度。

把剪切流速的定义式代入上式，可以得到另一种表达方式

式（3-40）中把水力半径、坡降等变量包含在u*之中。由于系数f是无量纲的，使得Darcy-Weisbach断面平均流速公式在量纲上比Chezy和Manning公式严谨。(https://www.xing528.com)

（4）对数型的明渠紊流断面平均流速公式。如果设全水深都是对数型式的速度分布，用第二章给出的二维明渠流动流速的沿垂线的分布公式（2-33）～（2-35），沿断面积分，即可以求出断面平均流速。对于明渠紊流，Kuelegan（1938）根据实测数据提出了如下的对数型断面平均流速公式

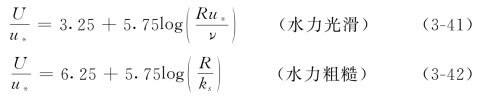
相应的床面水力光滑、水力粗糙情况Einstein统一公式为

其中χ的值由图2-5确定。

（5）Manning-Strickler公式。Strickler（1923）把Manning系数n用床面粗糙尺度ks来表达。他令ks=D65，提出了如下流速计算公式

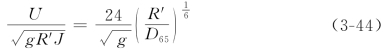
式中：是沙粒阻力对应的剪切流速；R′是沙粒阻力对应的水力半径。

（6）各公式的阻力系数或粗糙系数之间的关系。对同一个明渠均匀流动，如果只存在沙粒阻力（床面无沙波运动），，则式（3-36）、式（3-37）、式（3-40）、式（3-43）、式（3-44）五个公式的结果应当相同，即

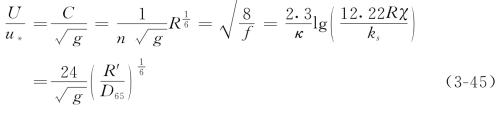
由此可得到Chezy阻力系数C、Manning糙率系数n、Darcy-Weisbach阻力系数f、对数公式中粗糙突起高度ks、床沙代表粒径D65五者之间的关系为

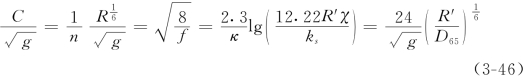
上式求出的Manning系数就是床面沙粒阻力对应的糙率nb。式（3-46）中包括了Kármán常数κ，它实际上是标志时均流速沿垂线分布状态的一个物理量。因此可以推知，阻力系数的变化与时均流速沿垂线分布的变化有关。由于时均流速沿垂线分布是由紊动状况所确定的，所以这实际上反映了阻力系数与紊动状况的关系。

（二）公式适用范围及粗糙尺度ks的确定方法

一般来说，上述的断面平均流速公式的适用条件是定床或床面平整、无沙波形态消长。由于速度沿垂线分布的对数型公式是在二维明渠流动中建立的，因此对数型的垂线速度分布积分得到的对数型断面平均流速公式，需经验证后，才能决定是否适用于棱柱形明渠，因为严格说来其中的流动不能认为是二维的。Kuelegan用试验证明了式（3-41）和式（3-42）对不同形状的断面均适用。他的试验结果如图3-23所示。可见（U/u*—5.75logR）先是随u*/ν的增加而增加（水力光滑区），然后逐渐与u*/ν无关而趋近于一个常数（水力粗糙区）。将式（3-41）和式（3-42）稍加改写后，即可知道此两式的预测与试验结果是一致的。由图3-23可见，粗糙突起高度ks相同、但过水断面形状不同的明渠流动的试验点据，基本上落在同一条曲线上。所以可认为，当坡降J、粗糙突起高度ks、水力半径R相同时，平均流速不因断面形态而异，可以用同一个对数型公式计算。

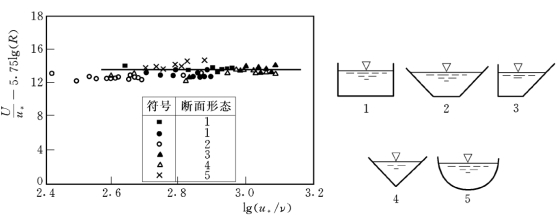
图3-23　不同形状断面明渠流的试验结果（Kuelegan 1938）

对数型的明渠紊流断面平均流速公式，由于引入了物理意义明确的粗糙突起高度ks，可以应用于边壁由颗粒组成的明渠流动，如床面由粗沙或卵石组成的天然河流，这也是对数型平均流速公式在含沙水流的流动阻力研究中应用较多的原因之一。由于天然河流河床上颗粒组成和排列的不规则性，此时公式中的ks不同于均匀、规则排列情况下的颗粒凸起高度，而是根据沙或卵石的粒径分布来确定的一个边壁粗糙尺度。对于床面由均匀沙组成的情况，ks就等于床面上的泥沙粒径D。对于床面由非均匀沙组成的情况，常选一个较粗的代表粒径作为边壁的当量粗糙尺度，如D65、D75、D90等。为了考虑床面起伏后大颗粒突出所造成的影响，边壁粗糙尺度ks应取得大一些，如3.5D65、3.5D75、2.5D90等。van Rijn（1982）收集了不同的研究者所用的当量粗糙尺度，如表3-4。可见ks的表达方式与各自研究的具体问题有关，各研究者之间并不一致。

如果床面是由粒径均匀、整齐排列的卵石组成的话，则ks就等于床面上的泥沙粒径D。如果床面不平整，有大颗粒突出，则按表3-4中Engelund-Hansen的方法，ks将相当于代表粒径D65的两倍。可见，边壁状况如是动床（床面有沙波），对数型断面流速公式中的边壁粗糙尺度ks就将更难以确定，明渠紊流的断面平均流速计算就会十分复杂。

表3-4　不同研究者所用的当量粗糙尺度

注　引自van Rijn（1982）。