床面运动特征分析

（一）沙波平均波长、波高与水流和泥沙条件的关系

（1）沙纹阶段。沙纹的波长、波高主要与粒径大小和流动的粘性底层厚度δ=11.6ν/u*有关。沙粒Reynolds数Re*实际上是泥沙粒径与粘性底层厚度之比，将试验结果用Re*和波长与粒径之比λ/D点绘所得到的关系曲线如图3-14。当Re*小于3.5时，λ与δ呈严格的正比关系，δ减小引起λ减小。Re*超过3.5后，δ的进一步减小反会引起λ的增加。显然此时沙粒已不再得到粘性底层的屏护，而是直接受到主流区紊动的影响，沙纹的发展可能由低频紊动控制，因而尺度会较大。

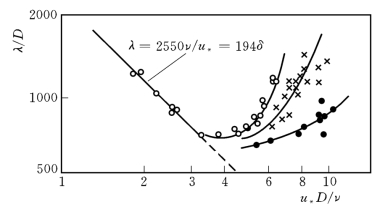
图3-14　沙纹的波长λ与Re*的关系（Yalin，1977）

（2）沙垄阶段。在沙垄阶段，推移质运动比较强烈，沙垄的发生、发展影响因素可用Shields数Θ、Froude数及相对糙率D/h来表达。Yalin和Karahan（1979）把沙垄的陡度Δ/λ（波高Δ与波长λ之比）的试验资料用相对Shields数（也称相对剪切应力）Θ/Θc（Θc是泥沙起动时的临界水流强度）整理如图3-15所示。

图3-15中可以看到随着水流强度的增加，床面从静平整到沙垄、再从沙垄到动平整的过程。沙垄的陡度Δ/λ的极限值为0.06。Garde和Albertson（1959）在沙纹阶段考虑了Shields数和Re*两者的影响，在沙垄阶段考虑了Shields数和Froude数两者的影响。由于其试验中水流强度的变化范围较小，Garde和Albertson没有给出从沙垄到动平整的变化过程。

图3-15　沙垄陡度与水流条件（Shields数）的关系（Yalin和Karahan，1979）

（3）沙粒阻力的概念。H.A.Einstein提出，床面的全部剪切力τ0中，只有一部分用于沙波的形成（也就是推移质的运动）。这就是所谓的“沙粒阻力”，它是水流与颗粒本身直接作用的结果。Engelund和Hansen（1966）把所对应的水流强度Θ′称为有效水流强度。在研究冲积河流阻力和推移质运动时，“沙粒阻力”是一个非常重要的基本概念。

Ranga Raju和Soni（1976）从研究推移质输沙率与沙波运动的关系入手，用沙波高度Δ、相对粗糙度D/Rb（Rb为从水力半径R中分割出来的与河床有关的部分）、Froude数Fr=U/和泥沙粒径D等参量与有效水流强度Θ′的综合关系处理试验和实测数据。他们的推导把沙波纵剖面简化为三角形，认为推移质单宽输沙率gb与沙波波高Δ和波速cs之间存在关系为gb=0.5γ′Δcs，其中γ′为床沙干容重，

式中：e为孔隙率。

引入如下的无量纲的推移质输沙强度参数Φ

其中利用了gb和γ′的表达式。Kondap和Garde（1973）认为沙波移动速度cs可表为

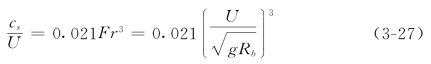
代入式（3-26）得

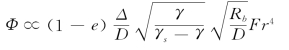
在一定条件下孔隙率可视为常数而归入比例系数。由于Φ主要由沙粒阻力对应的有效水流强度Θ′所决定，可以通过点绘原有试验结果来找出Φ与Θ′的关系

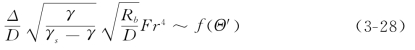
用上述参数点绘的Δ和λ的试验结果如图3-16（a）和图3-16（b）。

图3-16　沙波尺寸与水流条件的关系（Ranga Raju和Soni 1976）

张瑞谨（原武汉水利电力学院，1961）从水槽试验和天然河流实测资料得到如下的沙波波高公式

van Rijn（1984b）针对低水流能态区和过渡区中的沙垄床面形态，提出了确定床面形态尺度的方法。在建立关系时采用了无量纲粒径d*和输沙强度参数T，其定义分别为

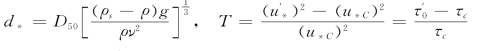
式中：u*C=（τc/ρ）1/2是按Shields曲线确定的床面临界剪切流速（其计算方法见第四章）；为相应于沙粒阻力的床面剪切流速。

的计算式为

C′为相应于沙粒阻力的Chezy系数。van Rijn利用水槽及原型资料确定了Δ/h、Δ/λ与T的函数关系，如图3-17。(www.xing528.com)

通过适线法。可分别得出关于Δ/h和Δ/λ的回归方程

上述两个方程都在T值大约为5时达极大值。从这两个方程还能推论出沙垄长度仅与平均水深有关，波长λ的表达式为

（二）沙波运动速度与水流和泥沙条件的关系

式（3-27）是典型的以Froude数为自变量的沙波运动速度表达式。类似的公式还有张瑞谨（原武汉水利电力学院1961）整理野外实测资料所得的关系式

及张柏年等整理长江实测资料所得关系式

式（3-30）和式（3-31）主要是用长江上的实测资料导出的。

由于沙波运动速度显然应与推移质运动强度有关，理论上应引入Shields数Θ和相对糙率D/h与Froude数一起作为变量来建立表达式，如Shinohara和Tsubaki（1959）所建立的沙垄运动速度公式

图3-17　沙波高度、陡度与输沙强度参数的关系（van Rijn，1984b）

（a）沙波高度；（b）沙波陡度

其中a及m的变化范围见表3-2：

（三）沙波运动与推移质输沙率的关系

泥沙颗粒在流体中的运动就其每个个体来说是随机的，但整体来看则是有明确的统计规律的。同样的道理，推移质的运动在微观上是每个泥沙颗粒的随机滚动或跃移，在宏观上则表现为沙波的运动。由于沙波的几何形态和运动速度是可以量测出来的，因而可以利用沙波运动的特点来估算推移质输沙率。

若以沙波波谷的连线为河床基准面，沙波在各点的高度为η，仿照式（3-7）有

表3-2　沙垄运动速度公式中a及m 的变化范围

式中：为床沙干容重；gb为以重量计的推移质单宽输沙率。

如果沙波的形状在运动过程中不变，则有

式中：c为沙波运动速度。

上式推导时用到了Δxη=cΔtΔη这一关系。联解方程式（3-33）、式（3-34），并令η=0处的推移质单宽输沙率为gb0，可得到一个波长范围内的平均推移质单宽输沙率为

式中：α为沙波的形状系数，对于三角形的沙波来说α=0.5；gb0与第一项相比可以忽略。Shinohara和Tsubaki（1959）分析了在河流及水槽中实测的沙波形态，认为α=0.55。再利用沙波的波高、波速与水流要素的关系式（3-29）和式（3-30），最后得到

式（3-35）的形式由张瑞谨（1961）提出。虽然这一推导方法物理概念比较清楚，但严格来说只有当沙波的纵剖面比较规则，且具有二维特征时才较准确。这一条件在小河溪内一般可以满足（能影响沙波发展的紊动能谱较窄，故沙波的波长分布也较窄），但在大的江河中紊动能谱宽广的多，因而沙波的能谱相应地也较宽，平面分布较为复杂，此时应用上述方法就较困难。尽管如此，式（3-35）对推移质输沙率的研究还是有极大的启发作用的。