床面形态的理论分析

床面形态与泥沙的输运有密切的关系，因此在分析床面形态时必须考虑泥沙的输运与水流的相互关系，这常常是分析的难点所在。

（一）时均流动条件下沙纹的成因

1.Exner的方法

Exner（1925）对单宽输沙率作了简化假定后，用泥沙和水流的连续方程联立求解得到了沙纹形成、发展的数学表达式。Exner使用的泥沙连续方程为

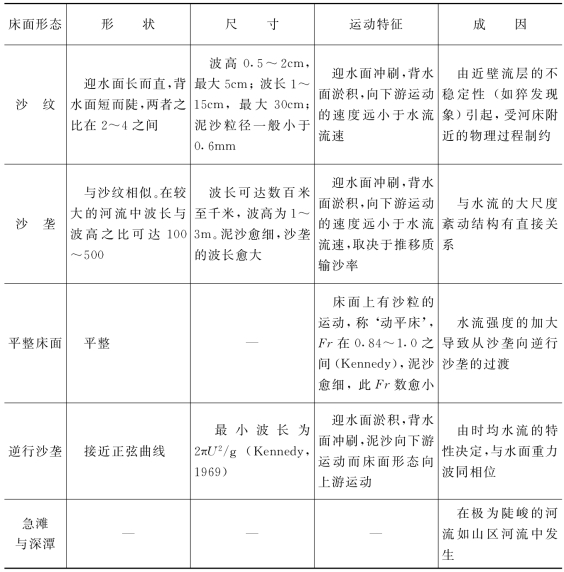
表3-1　冲积河流床面形态的分类与特性

式中：γ′为泥沙干容重；y为床面高程；x为沿流向的坐标；gt为单宽输沙率（按重量计）。

水流连续方程为

式中：Q为流量；Y为水面高程；B为河宽；U为平均流速。

对输沙率所作的假定为

式中：α与泥沙的干容重成线性关系。

把输沙率gt的表达式和用水流连续方程解出的U的表达式代入式（3-7）可得

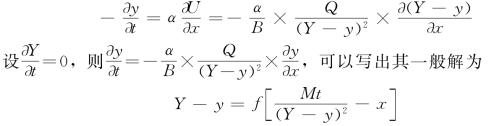
式中：f为一任选函数。

如果假定在t=0时的床面起伏形状为余弦曲线，即y=A0+A1coskx，则在任意时刻t，床面的形状将为

据此可绘出沙纹的演化过程。

Exner的分析在涉及到物理过程时处理得较粗糙，如输沙率与时均流速的一次方成正比与实际情况不符，不考虑沙纹形成过程中的力学机制等。

2.Bagnold的分析

Bagnold（1956）从受力平衡的角度出发，认为床面处于静止状态的颗粒摩擦力与水流及其携带的泥沙所施加的动摩擦力平衡时，河床保持平整，否则床面将出现沙波来增加阻力，与水流及泥沙的作用力平衡。据此他提出了河床保持平整的条件为

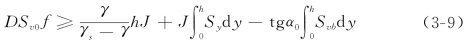
而形成沙纹的条件为

式中：D为泥沙粒径；f为静摩擦系数；Sv0为床面静止沙粒的体积比含量；Sv、Svb分别为在高程y处的全沙及推移质含沙量（以体积比计）；tgα为高程y0处颗粒剪切力与颗粒间离散力的比值，相当于一种动摩擦系数，其变化范围在0.32～0.75之间。可见，泥沙颗粒愈细，愈容易形成沙纹。

Exner和Bagnold的分析都是对于床面形态处于沙纹阶段的情况，但并未给出一个明确的条件来判别和区分沙纹和沙垄阶段。

（二）沙垄及沙浪的成因

可以仿照紊流理论中流动稳定性的线性理论来分析沙波的形成，先假定床面上有微小的起伏（微幅波），再用数学方法探讨在何种条件下微幅波振幅随时间增长或衰减。分析手段类似于波浪理论中的线性波理论（或称微幅波理论，Linear Theory of Waves/Theory of Small Amplitude Waves），即假定水流为无粘性的，且存在势函数，从Euler方程和水流连续方程出发分析波的运动过程。

Kennedy（1969）假定水流为二维势流，势函数为Φ，将连续方程中的流速用势函数表达可得Laplace方程

如果水流可以看成是速度为U的势流，则水面及床面都分别相当于一条流线。此时的水流流态对应于一明渠流动（此明渠流的水面距参考平面距离为H），河床床面则相当于距水面h处的一条流线（见图3-5），势函数遵循拉普拉斯方程。Kennedy把水面和河床床面作为流线处理，即它们都是流函数为常数的曲线，而流函数则是式（3-11）中流速势的共轭函数。方程式（3-11）在水面和床面的边界条件分别为：

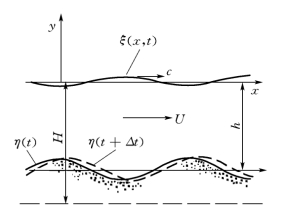
图3-5　Kennedy理论分析图解

（a）自由水面处

流速与水面相切，运动学条件为(www.xing528.com)

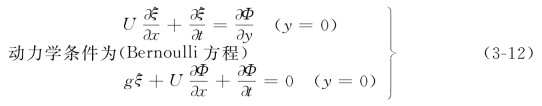
（b）河床床面处

与床面垂直的流速为零，运动学条件为

河床的初始微起伏为

水面的初始微起伏为

式中：a（t）和A（t）分别为沙波及水面波的波幅，两者初始相位相同；c为沙波及水面波的运动速度；κ为波数，κ=2π/λ；λ为波长。设水面波动可按水深为h的平底明渠流求解。

当沙波的波速c远小于时均流速U时，Kennedy得到满足上述边界条件的流速势Φ为

沙波与相应的水面波的振幅比为

Kennedy假定某一断面上的挟沙能力与该断面上游δ处的底流速的n次方成比例，即

其中比例常数m、指数n和滞后距离δ的数值取决于水深、流速及流体和固体颗粒的性质。由式（3-14）的流速势得到流速，与挟沙力式（3-16）一起代入泥沙连续方程式（3-7），可解得沙波的波速及振幅分别为

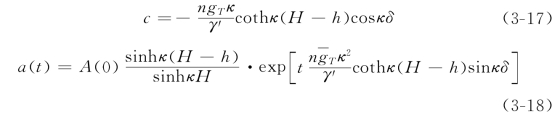
式中：为平均单宽输沙率；=mUn，U为时均流速。

当水流条件、泥沙颗粒性质和泥沙输运条件相同时，在所有波数的微幅波中，波幅的发展变化与波数κ（正比于波长的倒数）的大小有关。用求极值的方法求t=0时波幅增加最快的微幅波波数κ，可得到κ所满足的方程，即

对上式给出的方程进行变换，写为左边是Froude数的形式如下

其中j=δ/h。满足这个方程的波数κ就是床面上最终形成的沙波的波数。式（3-19）的图解见图3-6。相应的沙波运动波速为

Kennedy由上述结果推论认为，沙波的波长的主要决定因素是水流Froude数、平均水深h及滞后距离δ（它是一个特定距离，表示水流挟沙力的变化与底流速变化间在时间、空间上的滞后）。沙波的运动速度除与h及δ有关外，还取决于单宽输沙量。

由式（3-15）可对水面波与沙波是否同相作如下的判别：

h＜H，水面波与沙波同相，沙波形态为逆行沙垄；

h＞H，水面波与沙波不同相（相差180°），沙波形态为沙垄；

由式（3-18）可判别初始起伏是逐渐增长为沙垄，还是趋于消失使床面保持平整；

根据式（3-20）右边的符号，可判别沙波运动的方向。

Kennedy的理论结果可绘图表达，见图3-6和图3-7。

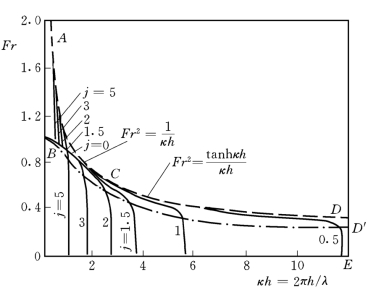
图3-6　Kennedy得到的Fr数与波长关系式（3-19）的图解（以j=δ/h为参数）

图3-7　Kennedy理论分析所得到的沙波分区（在Fr—j平面上表示）

在Kennedy的分析中，输沙率的变化和床面局部流速的变化往往不是同步相对应的，而是存在一个所谓“相位差”。对于Kennedy的分析，不少研究者作了进一步的补充。林泰造（Hayashi 1970）在挟沙能力方程中考虑了沙波形状的影响。Yalin（1973）利用Kennedy的结果，结合进一步的分析，对沙垄波长提出了估算方法。Parker（1975）则考虑了用泥沙颗粒的惯性来解释水流与泥沙运动的相位差。