有细沟坡面流动的基本方程

（1）动力波模式。描述非恒定渐变明渠流动的一维总流运动方程（St.Venant方程）和连续方程一起被称为动力波模型。对于流域内坡面上细沟较为顺直、均匀的情况，可以对每条细沟所控制的条形坡面上的流动建立一维总流方程。由于净雨强随时间的变化及沿程入汇，以及地形、粗糙度的沿程变化及摩阻坡降与地表坡降的不同，坡面流动一般是非均匀、非恒定的，动力波模型可以将这一性质考虑在内。

对于图2-25（a）所示理想化坡面上净降雨产生的细沟径流，设细沟间地表有一倾向于细沟的坡度，横向汇流长度与坡面长相比很小，因而横向汇流足够快。令点[x，t]处细沟内水深为h（x，t），流量为Q（x，t），细沟的过水断面A（x，t）=A[h（x，t）]，湿周为P（x，t）=P[h（x，t）]，h为垂直于平均坡面的水深，如图2-25（b）所示。细沟过水断面的形状可以是任意的。

设雨水落入细沟或横向汇流汇入细沟时水体速度的大小、方向与沟内水流相同，则任意断面非棱柱形细沟中完整的非恒定非均匀流方程为（Mahmood和Yevjevich，1975）

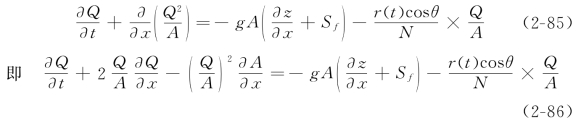
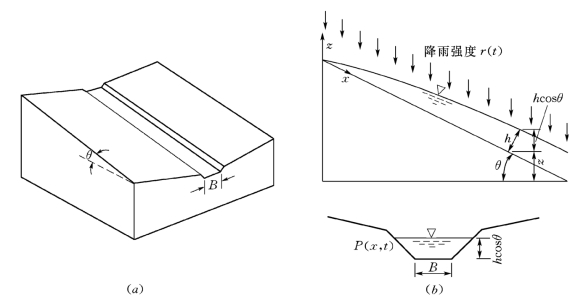
图2-25　理想化坡面上净降雨产生的细沟径流

（a）简化细沟示意图；（b）降雨形成细沟流示意图

式中：z为水面高程，z=Z+h/cosθ；Z为细沟沟底高程；h为垂直于坡面的水深。可见，细沟侧入流对动量方程的推导及最终形式也有影响，而不是仅仅局限于对连续方程的影响。为了便于与运动波方程比较，把过水面积A写为水深h的函数，由式（2-86）变换可得

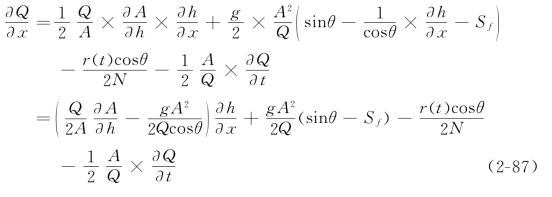
代入连续方程

后即可得到如下的特征方程组

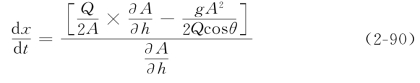
上两式也可写为

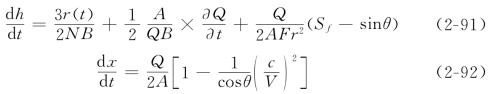
式中：Fr2=为Froude数的平方；c=为微波波速，B对于已知断面形状，或已知面积A、湿周P随水深变化的函数关系，可以求出特征方程的具体形式。式中的导数∂Q/∂t沿流体质点的运动轨迹应按Lagrange法理解。

（2）运动波模式。平面漫流的运动波模型在一些以坡面物理过程为基础的坡面流动和侵蚀机理模型中有广泛的应用（Rose et al 1983，Kirkby 1990，USDA 1995）。运动波模型最早是应用于河流中的洪水演进（Lighthill&Whitham 1955），随后又应用于坡面为平面时的坡面流动计算（Henderson&Wooding 1964）。Kibler&Woolhiser（1970）用运动波模型建立了“梯级跌水”式的坡面产流模型。Tayfur和Kavvas（1994）分析细沟间坡面漫流时也采用运动波模型作为动量方程。在坡面流动的数值模拟研究中，也有人采用平面漫流运动波模型计算矩形断面细沟内的流动（Baird et al 1992）。

沿用前述对坡面地形的简化假设，并设雨滴速度对沟内水流影响可忽略，可以推导得到任意形状断面细沟内一维总流的运动波模型的连续方程和运动方程分别为

其中N为坡面上单宽（y方向上单位长度）内细沟的数量，单位是1/m，式（2-93）右边项的意义为单位时间内单位宽度坡面上的降雨量除以细沟数量，其单位是[m2s—1]。当细沟底宽等于1/N（m）时，流动为无细沟的坡面漫流。其特征方程组为

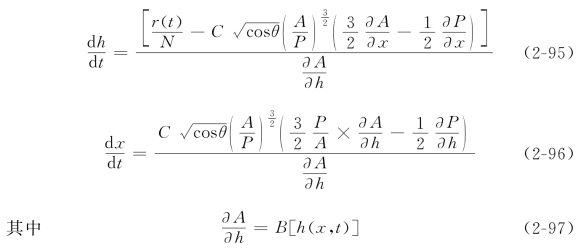
在断面形状对称，且边坡近似为平面的情况下，有(www.xing528.com)

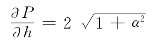
其中α为细沟的边坡坡度。对于断面形状沿程变化不大的情况，认为

则式（2-95）可简化为

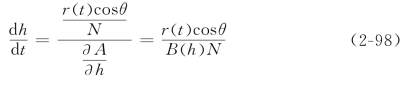
对于已知断面形状，或已知面积A、湿周P随水深的变化的情况，可以求出特征方程的具体形式。例如，对于矩形、三角形、梯形三种简单几何形状，其特征方程的具体形式如表2-4。

动力波方程式（2-89）中，细沟侧入流、流动的非恒定性、流动的非均匀性对流动的影响分别反映在右边第一、二、三项中，与运动波模型的方程式（2-95）相比有明显的差异。当净雨强较大时，Q也较大，方程式（2-89）中右边第二、三项对两种模型差异的影响会减小，而第一项侧入流的影响会增大。净雨强较小时，第一项侧入流的影响会减小，右边第二、三项（地形、粗糙度的沿程变化及摩阻坡降与地表坡降的不同）对两种模型差异的影响将会比较突出。这将导致运动波模型和动力波模型对坡面流动的计算结果上的差异。

（3）运动波和动力波模型数值解结果比较。式（2-89）、式（2-90）右边含有非线性项，较难求得精确解，但可以采用数值计算方法求出近似解。以下的计算中采用了不同大小的稳定净雨强以比较其对计算结果的影响，其取值范围为2.5～20 mm/min。这种净雨强有一定的持续时间，坡脚处产生径流后其流量将持续增加，一般会达到一个稳定的流量值。两种模型得出相同的稳定的流量值，但却给出了不同的水深及流速值。

表2-4　过水断面为简单几何形状时运动波模型的特征方程

上述的运动波模型和动力波模型在计算图2-25所示的理想化坡面上产生的径流时采用如下条件：单宽（1m）内细沟的数量为1，细沟断面形状为梯形，令细沟底宽B的变化范围为0.05～0.9m，以便于比较细沟底宽B对计算结果的影响。忽略入渗过程，只考虑净雨强。为了模拟短时段实测暴雨净雨强，令净雨强过程持续5min稳定不变，5min后净雨强为零。计算中采用不同大小的稳定净雨强以比较其对计算结果的影响。在稳定持续的净雨强下，坡脚处达到的稳定流量值大小是由连续方程所决定的，因此两种模型所得到的坡脚径流稳定流量值必然相等，但两种模型所给出的到达稳定值所需时间会有不同（也就是径流过程线形状不同）。这是由于径流水深、流速与坡面上细沟宽度和净雨强的关系是由动量方程所决定的，既然两种模型的动量方程完全不同，则两种模型得到的径流水深、流速也将显著不同。图2-26所示是对长度为50m的坡面按10mm/min持续净雨强进行计算、当坡脚处径流流量稳定后得到的坡脚径流流速值，可见两种模型的差异是明显的和系统性的。这一差异必然导致径流过程计算结果的不同，主要表现在两种模型计算出的坡面流动水深及流速有明显差别，而且这一差别与坡面上细沟宽度及净雨强的大小相关，分别讨论如下。

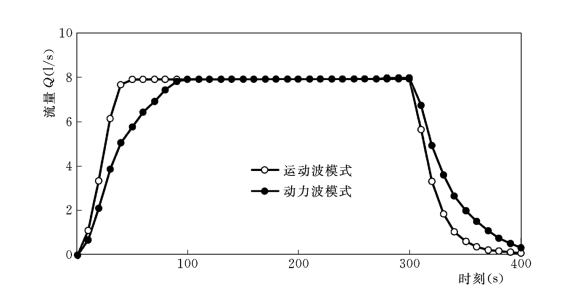
图2-26　出流流量全过程模拟结果。净雨强r（t）=10mm/min，持续5min，坡度15°，坡长L0=50m，小区宽5m，细沟底宽0.2m，阻力系数C=20。

1）坡面径流水深H与细沟宽B和净雨强的关系：图2-27（a）所示为2.5mm/min净雨强下，出流水深h与细沟底宽B的关系。对于常见的短时段暴雨净雨强（大小为1～3mm/min），运动波模型和动力波模型给出的坡面流动水深计算结果差异主要依细沟的底宽B而变。

以持续5min、大小为2.5mm/min的恒定净雨强在倾角为30°的5m长坡面上产生的径流为例，坡面细沟越窄，运动波模型和动力波模型对坡面流动水深和流速计算结果的差别越大。

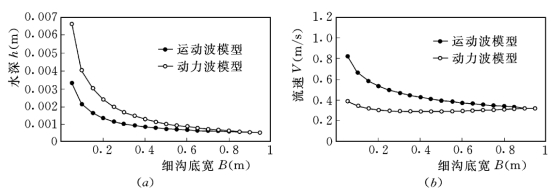
图2-27　运动波和动力波模型数值解结果比较（恒定净雨强2.5mm/min，坡面长5m，倾角为30°）

（a）坡面径流水深h与细沟宽B的关系；（b）坡面径流流速V与细沟宽B的关系

在细沟宽度为15～20cm的典型情况下，动力波模型计算得到的水深为运动波模型的两倍。这说明动力波模型方程式（2-89）中考虑了侧入流及摩阻坡降与地表坡降的不同后，所给出的径流水深值较大。从物理意义上看，相当于在计算结果中增加了径流过程中的坡面槽蓄量。运动波模型未考虑上述因素，其水深计算结果偏小，相当于在计算结果中采用了较小的坡面槽蓄量。

在计算条件下，当细沟宽度接近极限值1m时，流动成为平坦坡面上的面流。对于2.5mm/min恒定净雨强的情况，计算得到的坡面流是较均匀的渐变流动，流动的水深小（1mm左右）、流速缓（0.3m/s），因此动量方程中反映非均匀性、摩阻坡降与地表坡降不同的项对水深计算的影响不十分明显，再加上此种净雨强下侧入流的影响相对不大，故两种模型对面流水深、流速的计算结果比较一致。

如果采用较大的净雨强，有细沟时两种模型对坡脚稳定径流深计算结果的差别更加明显。在20mm/min的净雨强下，即使在计算中所取的细沟宽度较大、径流成为坡面漫流的情况下，动力波模型得出的稳定水深仍然超出运动波模型计算值一倍左右。这是由于较大的净雨强下，动力波模型动量方程中反映侧入流、流动的非均匀性、摩阻坡降与地表坡降不同的项对水深计算产生的影响是不可忽略的。

2）坡面径流流速V与细沟宽B和净雨强的关系：当坡脚处径流流量达到稳定时，由于水流连续条件的制约，径流深度的变化会引起径流流速向相反方向变化。图2-27（b）所示为两个模型所得到的径流流速与细沟底宽B的关系。对于2.5 mm/min恒定净雨强的情况，坡面无细沟（即计算沟宽与坡面宽度接近）时，两种模型的流速计算结果十分接近，而当坡面细沟底宽小于0.3m时，运动波模型计算得到的坡面流速明显偏大。由同一图中可见在这一净雨强值下，动力波模型得到的径流流速在不同的细沟底宽条件下的变化幅度较小。因此，若动力波模型得到的径流流速接近实际情况，则坡面无细沟（或无集中水流）时，可以认为运动波模型所给出的径流流速计算值是比较准确的。但对于坡面有细沟（或集中水流）的情况，若用运动波模型按细沟径流计算流速则得到大于实际情况约一倍的值。此时若假设流动为坡面漫流，则相当于将细沟中的实际流速等同于整个坡面上的面流流速，从而将会夸大坡面上发生此流速值的面积范围。

流速的模拟结果与水深计算有类似的变化趋势。当净雨强增加后，两种模型所得到的坡脚稳定径流流速的差别明显加大。对较大的净雨强，即使在计算中细沟很宽、径流成为坡面漫流的情况下，运动波模型得出的稳定流速仍然超出动力波模型计算值一倍左右。