坡面薄层水流的流态与流道分析

根据水动力学原理，水流的流动型态由Reynolds数Re=UR/ν判别。对薄层水流来说有R≈h，所以薄层水流的Re数可表为

式中：q为单宽流量。

姚文艺（1996）用人工降雨水槽试验对坡面流的阻力规律进行研究，点绘了坡面流的Darcy-Weisbach阻力系数f与Reynolds数的规律，发现点据呈现出明显的分区规律，似乎说明有降雨下的坡面流也存在着层流、紊流和过渡流。然而，试验观察又表明，即使雷诺数处于层流区范围，注入到水流中的示踪剂沿垂向和横向均有一定扩散。另外，当水深较小时，降落的较大雨滴甚至可以将水流溅开使床面瞬时露出，坡度越小，这种现象越明显。因此姚文艺认为，虽然水流的Re处于通常的明渠层流区范围，Darcy-Weisbach阻力系数f也遵循Re的负一次方关系，但是降雨已经使水流受到一定的扰动。此时，根据Re及其与f的关系所判别的层流与通常定义的层流概念并不相符。对这种降雨扰动了的径流应称之为“伪层流”，另外两种流态仍称为紊流和过渡流。

从理论上讲，将“伪层流”称为“扰动流”有其不合理之处，因为“扰动流”一词不能明确表达上述降雨影响下薄层水流所处“层流”流态时的力学现象。实际上，只要有一定强度的降雨，无论水流处于何种流区，都会受到扰动，成为扰动流。因此，“扰动流”的概念不够明确，以称“伪层流”较恰当。

坡面流处于“伪层流”时，尽管雨滴已对水流有所扰动，水质点有局部掺混现象，但由于Re与f的关系仍符合在通常明渠层流内的变化规律，表明此时水流的粘滞力的作用仍大于惯性力的作用，整体水流仍处于层流状态。从阻力系数f与Re数的规律中可见，伪层流的临界Re随坡度的增大而有所减小，平均而言约为800，紊流的临界Re数约为2000。与坡面均匀流相比，在相同的单宽流量下，有降雨时的沿程变量流会较早地进入紊流。

吴长文、王礼先（1995）为了研究林地坡面的水动力学特性，采用针头式人工模拟降雨和摆喷式人工降雨机分别进行了集水小区试验，并取临界Re数为500。采用针头式人工模拟降雨的集流小区的坡角为α，坡长为40cm，水平投影面积为160cosαcm2，雨强恒定在1.0mm/min左右。降雨均匀度在0.9以上。采用摆喷式人工降雨小区的坡角为α，坡长为L=6m，集流面积为36cosαm2，每场试验为恒定雨强，不同的降雨场次雨强在1.86～2.3mm/min，降雨均匀度在0.8～0.96之间。试验集流小区的坡度在22°～33°之间，按坡面水动力学划分（α＞3°为陡坡）属陡坡。试验中实测的坡面流Reynolds数如表2-3所示。由表2-3可看出，无细沟股流情况下坡面流最大Reynolds数Re小于临界数500。根据单宽流量与Reynolds数的关系由式（2-79）可知，若净雨率为1.0mm/min，则只有当坡长的水平投影为30m时才能使Re=500。(www.xing528.com)

对比1992年实测的一次天然降雨林地坡面流情况，暴雨约为20年一遇（15min雨强I15=1.38mm/min），由刺槐林小集水区试验测得的刺槐林地峰值流量系数φ15=0.315，若按不出现细沟集中流的理想平整坡面计算，只有当坡长L＞69m时，才达到的坡面流临界Reynolds数500。因此若按无细沟股流来判别流态，则一般的林地和裸露坡面流均是层流。由层流理论可知，流体的层流运动与其粘滞系数有关，而与固体边壁的粗糙度无关，这显然与自然坡面水流的实际情况大相径庭（吴长文、王礼先，1995）。

表2-3　摆喷式人工降雨试验中林地坡面水流的Reynolds数（小区出口处）

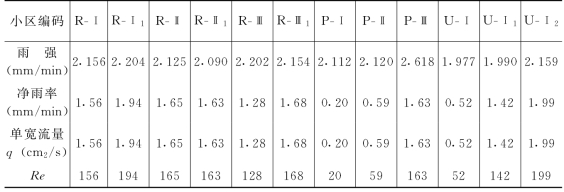
注　引自吴长文、王礼先（1995）。R、P、U分别表示刺槐、油松和对照荒草坡；Ⅰ、Ⅱ、Ⅲ分别表示小区编号，下标“1”表示相应小区搂去枯落物处理小区，“2”表示铲去表层有机质。

沙际德、蒋允静（1995）认为，坚实光滑土渠的曼宁糙率n最小为0.016，相应的表面绝对的突起高度仍约为ks=4～5mm，而天然土坡或裸地的突起高度通常在10mm以上。显然，这样大的突起，深度仅为0.5～2.5mm的薄层水流不可能漫流于全部坡面，它必然选择发育流道、绕道而行的方式。虽然，流道的出现增加了流程，但流道内的床面突起却比地表大为“光滑”了。试验表明，即使人工特意制作的定床坡面，也只有当水深大于突起高度的4～5倍时，才可能使水流较为均匀的布满全坡。在初生态侵蚀区，降雨后的地表积水深度一旦超过微地貌制约高度（有效突起高度），水体的“溢流”与“集聚”必然随之而生，由于地表突起的时空随机性，“溢流”与“集聚”宏观上顺坡而下，但其演变过程受制于输水、挟沙、耗能三种非谐调机制的共同作用，因之，流道趋于选择阻力最小的流相（平面与断面形态），故呈现出兼并、摆动等横向不稳定现象。

如果坡面流动中实际都是“流道流动”，则其流动Reynolds数将大大高于理想的全坡漫流。例如，设集水小区坡面的横断面上，流道所占宽度为断面宽度的1/10，则前述人工降雨小区的坡长水平投影为3m时、天然降雨林地坡面长度大于7m时，出口即可达到紊流状态，而不是全坡漫流假设下的30m和69m。

在一般的河流泥沙运动理论中，把泥沙运动划分为推移质和悬移质（跃移质则介于二者之间）。水流挟带悬移质的理论是基于紊动扩散的概念，即悬移质是依靠水流紊动所形成的涡体引起水团的上下交换所致。如果按坡面漫流计算，则由Reynolds数判别准则得出在一般的坡面流中均为层流，并无涡体存在。由此推论，坡面水流的泥沙运动只能以跃移质或推移质形式运动，没有悬移质运动所需的紊动能量。而实际上，野外坡面，尤其是有枯落物的林地坡面的粗糙度很大，而水层又相对很薄，因此与理想的管道流或具有一定水深的明渠流流态判别方法应有所不同。层流之所以失去稳定而变为紊流，主要是由于水流在行进中不可避免会受到一些超过一定限度的干扰，局部扰动会引起涡流，坡面流动中的各种干扰显然是较大的。吴长文、王礼先（1995）由此推论在降雨条件下自然坡面水流保持层流的条件是不存在的。况且，即使是层流运动，并不是绝对不允许降雨条件下的坡面水流中有悬移质泥沙运动，因为极细的泥沙颗粒在雨滴击溅作用下，飞溅进入水层，其沉降速度是很慢的，随着雨滴的不断击溅，更多的细颗粒泥沙进入水层，故而击溅扰动可以增加薄层水流的混浊度（含沙量）是无疑的，击溅扰动是否增加水流紊动的争议并不影响这一点。因此，一般不认为坡面薄层水流是纯粹的层流运动，亦不是充分紊流，而是一种介于它们之间的流动。