明渠紊流结构在非恒定条件下的变化特点

天然河流中的水流运动一般是非恒定或非均匀的，如洪水期间的涨水或落水（非恒定）、河道的扩宽与收窄（非均匀）等。了解非恒定、非均匀条件下明渠紊流的结构，对研究天然河道中的泥沙输运和河床演变有重要意义。随着试验技术的不断改进，在非恒定、非均匀明渠紊流试验研究方面已经积累了一些资料，但总的来说还有待于进一步深入研究。

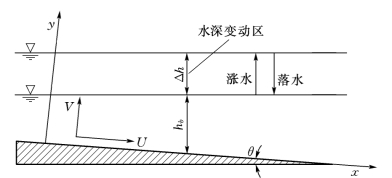
图2-14　非恒定条件下的明渠紊流示意图

（1）基本方程和非恒定参数。图2-14所示非恒定条件下，明渠二维紊流的控制方程为

式中：τ是总剪切应力，τ/ρ≡+ν∂U/∂y；U、V是时均速度分量；u、v是脉动速度分量；θ为明渠渠底与水平面的夹角；x、y分别与渠底平行和垂直，y的坐标原点在渠底上；P为时均压力，可以近似认为它遵循静压分布。所以由式（2-59）可得如下近似式

由式（2-58）和式（2-60）可得

式中：h为水深。将式（2-61）从y积分至水面（y=h），可得与渠底距离为y处的总切应力为

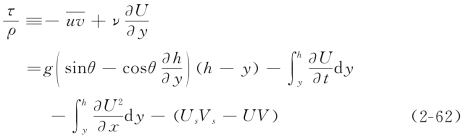
式中：下标s表示自由水面处（y=h）的值，由于Vs=∂h/∂t，上式可简化为

在式（2-63）中令y=0，则可得到床面切应力τB和剪切流速u*如下

Neze等人（1993）根据试验结果认为上式右边第三项与前两项相比可以忽略，因而床面切应力可以用下式计算：

(www.xing528.com)

式中采用水力半径R是为了考虑边壁影响，B为水槽宽度。Nezu等人的试验结果显示，式（2-64）右边第一项在涨水阶段的值大于落水阶段，而第二项的变化方向则与第一项相反。

为了便于比较光滑床面和粗糙床面上的非恒定流动特性，可以利用外区变量，定义如下参数α来表征流动的非恒定性质

式中：Td是从基流流量升至洪峰流量的历时；下标p和b分别表示基流（base）和洪峰（peak）时的量值；Uc是紊动涡旋的迁移速度，近似等于（Ub+Up）/2。在明渠流动中，非恒定性参数α与压力梯度dP/dx有关，也可以认为α对应于封闭管道周期性震荡流动中的表征震荡周期特性的Strouhal数。

（2）床面切应力及剪切流速的确定。Nezu等人（1997）采用二维激光流速仪对非恒定紊流的时均和脉动特性进行量测。测定时均流速时采用了Fourier级数法，即将流速变换为离散Fourier级数和的形式，项数取为7项，通过只计入低于一定频率的分量来确定时均流速。通过量测粘滞底层（y+＜8）内的流速分布，并用最小二乘法确定回归方程U=ay+by2的线性项系数，根据该系数值计算粘滞底层的剪切流速和Kármán常数κ（试验结果显示κ值在非恒定流动中亦为一个常数0.41）。进一步根据κ值和实测的对数区流速分布，由对数定律确定剪切流速，结果证明它等于依据粘滞底层的流速分布所确定的剪切流速。

（3）紊动强度及Reynolds应力的量测。由于流动的非恒定性，Nezu等人（1997）在测定脉动强度时采用短时段平均法，将每个涨水、落水循环分成20个时段，统计出每个时段内的紊动强度及Reynolds应力分布。试验结果显示，如果用相应的剪切流速对各短时段的脉动强度和Reynolds应力进行无量纲化，则无量纲的脉动强度各分量及Reynolds应力在涨水时段和落水时段的分布基本是相同的，涨水时段和落水时段可以采用同一个方程式。在水深变动区，紊动趋于各向同性（脉动强度的两个分量基本相等）。Nezu等人的结果还表明涨水落水段无量纲总紊动强度均低于恒定、均匀明渠流动中的情况（图2-15a），这明显有别于封闭管道中非恒定流动的试验结果。另据Tardu等人（1994）的结果，封闭管道中震荡流动条件下，近壁处的纵向脉动强度略高于恒定管道流动的情况。

采用对数—尾流定律式（2-32），代入式（2-10）可得恒定情况下Reynolds应力的分布为

在外区（ξ=y/h＞0.2），上式第一个等号右边的第二项可忽略。当Reynolds数较小时，第三项也可忽略，因为此时∏≡0。因此恒定流动中，除了靠近边壁处外，Reynolds应力的分布是线性的。由图2-15（b）可见，在非恒定流动中实测的Reynolds应力分布，尽管点据有一定散乱，仍然很好地遵循线性分布，即使在水深变动区也符合良好。这说明经壁面切应力无量纲化的Reynolds应力分布受流动非恒定性的影响是不显著的。这与Tardu等人（1994）的试验结果是一致的。

图2-15　非恒定明渠紊流（涨水段）的脉动强度和Reynolds应力与恒定流情况（图中实线，Nazu&Nakagaw a1993资料）的对比

（a）脉动强度；（b）Reynolds应力

图2-16为均方根脉动流速及Reynolds应力的涨水段实测值和落水段实测值之比。其中下标r表示涨水段（rising，0＜T＜1），f表示落水段（falling，1＜T＜2）。由图中可见，在基流深度（y＜hb），涨水段的脉动强度和Reynolds应力均大于落水段，随着非恒定性参数α的增大，两者比值略有增大。变化较为显著的是水深变动区（y＞hb），在此区域内，涨水段和落水段脉动强度的比值首先增加，达到一个极大值后又迅速减小，在自由水面处涨水段的脉动强度小于落水段。Reynolds应力的变化过程也是类似的。

图2-16　涨水段、落水段的脉动强度和Reynolds应力对比

（a）脉动强度；（b）Reynolds应力

Song和Graf（1996）对粗糙床面上的非恒定紊流的时均和脉动特性进行量测时，采用了超声多普勒流速仪（acoustic Doppler velocity profiler，ADVP）。其试验结果同样显示涨水段的脉动强度和Reynolds应力均大于落水段。