紊流的时均及统计特征值分析

（一）时均特征值

明渠紊流流动的试验测量首先要确定一些重要的时均及统计要素或其空间分布，如剪切流速、时均流速分布、脉动流速均方根值分布等等。

（1）剪切流速u*。对于明渠二维紊流来说，剪切流速u*是一个基本速度比尺，需要精确地测定。恒定均匀流动中u*可以通过下面5种方法之一来确定（Nezu&Nakagawa 1993）：

1）在恒定均匀流动中，dh/dx=0，由式（2-11）得u*=（g RJ）1/2，其中R为水力半径，对于明渠二维紊流来说R=h；

2）量测时均流速沿水深的分布U（y）后，假定κ=0.4，由式（2-29）反算得到u*；

3）量测Reynolds应力—及时均流速U（y）沿水深的分布后，由式（2-10）反算得到u*；

4）如果粘滞底层存在并可以量测出其中的流速分布，则可由式（2-28）反算得到u*；

5）可以使用Preston管间接量测壁面剪切应力来确定u*。

Preston管是外径为dp的圆形Pitot管。可以证明它置于边壁上时，总压头pt、静水压头ps、流体密度ρ、运动粘滞系数ν、边壁剪应力τ0，以及dp等变量遵循如下关系（Preston1954）

根据Preston管原理测出的剪应力分布表明，从明渠边壁上的水边线起到渠底，剪应力逐渐增大，从（0.6～0.8）γRJ增至（1.0～1.2）γRJ（Ippen&Drinker 1962，Replogle&Chow 1966）。

（2）壁面定律及主流区速度分布。对壁面附近流速分布的不同量测表明，壁面定律的Kármán常数κ和A有稳定的数值。一些量测的结果如下：

κ=0.41，A=5.0（边界层流动，Coles 1968）

κ=0.41，A=5.17（封闭管道流动，Dean 1978）

κ=0.41，A=5.2（边界层流动，Brederode&Bradshaw 1974）

κ=0.41，A=5.29（明渠流动，Nezu&Rodi 1986）

实测结果表明，外区的流速分布与对数分布式（2-29）存在系统偏差，当Reynolds数足够大时，在自由水面区域（y/h＞0.6）这种偏差很大，不能忽略。对于特定试验条件，通过选取合适的∏值（Coles尾流强度参数）代入尾流函数式（2-31）中，就可以使外区的流速分布式（2-30）与实测数据较好地符合。Nezu&Rodi（1986）在明渠流动试验中得到的∏值随剪切Reynolds数R*≡hu*/ν而变，R*＜500时∏≈0，500＜R*＜2000时∏值迅速增加，R*＞2000后∏值稳定在0.2左右。

（二）紊动统计特征值

（1）脉动流速均方根（脉动强度）值和Reynolds剪切应力。图2-8所示是根据明槽水流试验和管道气流试验（Laufer 1954，Clark 1968）测得的纵向、垂向和横向脉动强度u′，v′，w′沿水深分布的点据，概化得到的三条曲线。图2-9为剪切紊流靠近壁面处脉动强度u′/u*的实测资料趋势线（分别引自Laufer 1954，Grass 1971，Nakagawa et al 1975等）。

图2-8　实测明渠紊流脉动强度分布

图2-9　壁面附近纵向脉动强度分布(www.xing528.com)

由这些量测结果可见，从主流区到近壁处，紊动强度不断增加，但在靠近壁面处，由于粘滞作用和固壁对紊动的衰减作用，紊动强度将急剧减小，在壁面上衰减为零。图2-9显示，边壁处纵向脉动强度为零，在离边壁不远处（y+=17）脉动强度迅速增加到最大值u′/u*=2.8，在主流区内又略有减小并接近于一个常数。这说明近壁层紊动能量的生成大于耗散，而主流区则是紊动能量的耗散大于生成。

图2-10是分别在光滑和粗糙床面上测得的靠近壁面处纵向、横向和垂向脉动强度u′、w′、v′（Grass1971，Nezu 1977）实测资料趋势线。由图中可以看到壁面粗糙高度越大，无量纲脉动强度的纵向分量u′/u*越小而垂向分量v′/u*越大。在明渠紊流中，当y/h＞0.3时，无量纲脉动强度的大小不受边壁粗糙大小的影响（参见Nezu&Nakagawa 1993，图4.7）。

图2-10　光滑和粗糙床面上靠近壁面处纵向、横向脉动强度（壁面粗糙顶部位置系指Nezu，1977资料）

（2）脉动强度计算式。Nezu&Nakagawa（1993，1997）根据明渠恒定均匀紊流的实测资料提出计算脉动强度沿垂线分布的经验公式如下

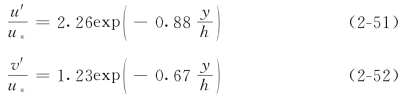
窦国仁（1983）由紊流随机理论出发导出的脉动强度分布公式为

式中：R*=u*Δ/ν是粗糙Reynolds数；y*=y/Δ是无量纲粗糙高度；Δ是粗糙高度。上式适用于光滑区、过渡区和粗糙区（aΔ＜y＜h，其中aΔ为粗糙后的分离层厚度）。当R*≤1.25时，Δ可从公式中消去（即，壁面粗糙是否存在对紊流结构无影响）。当R*≥100时，公式中应以R*=100代入。

（3）二维明渠流动中的涡粘性系数νt（eddy viscocity）。图2-11所示为由实测资料得到的无量纲涡粘性系数νt/（hu*）趋势线，分别来自明渠流动试验（Jobson&Sayre 1970，Ueda et al 1977，Nezu&Rodi 1986）及封闭管道试验（Quarmby&Quirk 1972）。图中ξ=y/h，h为水深，同时标明了尾流函数中的∏值。所用的涡粘性系数νt曲线方程为（Nezu&Rodi，1986）

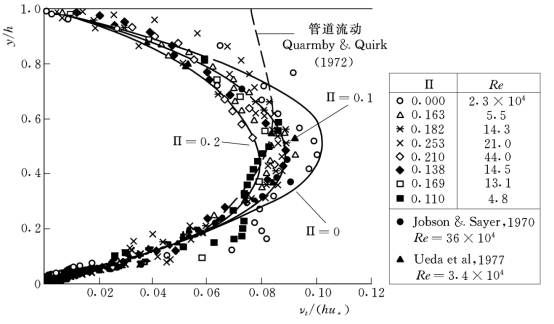
图2-11　明渠实测无量纲涡粘性系数νt沿水深的分布

（4）二维明渠流动中的混掺长度l（mixing length）。图2-12为由明渠紊流试验实测资料得到的无量纲混掺长度l/h沿水深的分布（Nezu&Rodi 1986），同时也给出了封闭管道紊流中得到的Nikuradse分布曲线（引自Nezu&Rodi，1986）。明渠紊流中无量纲混掺长度l/h沿水深的分布所采用的方程为

其中衰减函数Г（ξ）的形式为

由图2-11可见明渠紊流的涡粘性系数在自由水面处明显小于封闭管道紊流的管道中心处，显示出自由水面处的紊动动量交换受到较大抑制。而从图2-12中的试验点据上尚不能明确得出自由水面处的混掺长度为零的结论。

图2-12　明渠实测无量纲混掺长度l/h沿水深的分布

（5）二维明渠流动中Reynolds应力沿水深的分布。图2-13所示为Nezu&Rodi（1986）实测的Reynolds应力沿水深的分布。由图中可见，在恒定均匀流动、Re数较大的条件下，距边壁较远处（y＞0.2h）呈线性分布，即方程（2-10）中的∂U/∂y项在主流区可忽略，只要依据即可得到总的切应力沿水深的分布，并可计算出u*的量值。

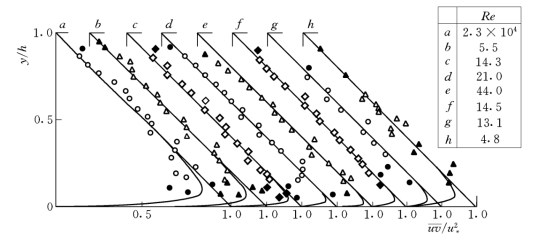
图2-13　实测Reynolds应力沿水深的分布（空心、实心点据代表不同量测方法）