二维明渠紊流流动由于边壁和自由水面的存在，在现象上表现出分区的特点。这除了可以作为描述明渠紊流性质的依据外，还可为方程组式（2-15）～（2-17）选择封闭方法和求理论解提供帮助。在不同的流动区域，必须为速度和长度选择不同的特征比尺，并用这些特征比尺将紊动特征量的表达式无量纲化以求得普适形式（universal expression）。
1.二维明渠紊流流场的分区
流速脉动谱的三个分区是紊动生成区、惯性区、粘滞区。在紊动生成区，时均流动中的能量被提取出来用于紊动能量的生成，然后传递给惯性区尺度较小的涡旋，最后在粘滞区耗散为分子热运动。壁面紊流场中的能量传递可以类比于这种能谱分区之间能量的梯级传递，因而二维明渠紊流流场也可以划分为三个子区域，如图2-4所示。这三个子区域分别是：
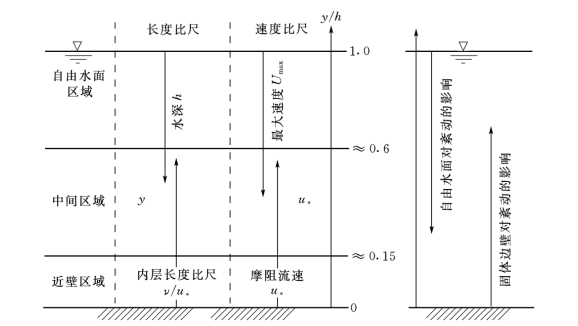
图2-4 二维明渠紊流流场子区域的划分
（1）近壁区域（Wall region）：y/h＜（0.15～0.2），这一区域对应于经典边界层理论分析中的内层（inner layer），其长度和速度比尺分别是ν/u*和u*。在壁面定律成立的范围内，紊动结构可用内层变量来表述。在距壁面较近的范围内（y+≡yu*/ν＜50）猝发现象极为剧烈，相应地在y+≤50的范围内紊动能量的生成超出了耗散（G＞ε）。
（2）自由水面区域（Free-surface region）：0.6＜y/h≤1.0，这个区域中的紊动结构是由外层变量来描述的，其长度和速度比尺分别是水深h和最大主流流速Umax。例如，这个区域的流速分布可以用“对数-尾流定律”来表示。在这个区域中紊动能量的耗散ε超出了生成G，因此紊动能量必须经由紊动扩散从壁面区域补充到自由水面区域。垂向流速脉动强度等紊动特征量受到自由水面的极大影响，这与封闭管道内的紊动现象是极为不同的。
（3）中间层（Intermediate region）：（0.15～0.2）≤y/h≤0.6，在这个区域自由水面和固壁的影响都不大，可以大致地把它类比于能谱中的惯性区。其长度和速度比尺分别是y和
。在这个区域中（包括壁面区域中y+＞50的部分）紊动能量的生成G与耗散ε近似达到平衡（G≈ε）。自由水面区域和中间层一起称为“外区（outer region）”或“外层（outer layer）”，在其范围内粘滞性的影响可以忽略。
2.壁面定律（the law of the wall）
壁面定律即固体边壁附近区域内、壁面法线方向（记为y方向）上紊流所遵循的时均流速分布规律，包括粘性底层、过渡区和对数区。在这个区域内的长度和流速分别用ν/u*和u*来无量纲化，从而得到所谓内层变量（inner variables）。对于光滑底面上的流速分布，可以在式（2-10）中代入Prandtl的混掺长公式，即
整理后即得到如下的无量纲流速梯度表达式
式中：ξ≡y/h，U+≡U/u*，y+≡yu*/ν，y+是用粘性长度尺度ν/u*无量纲化的长度，R*≡u*h/ν是用摩阻流速和水深得到的Reynolds数，l+≡lu*/ν是无量纲混掺长度。如果无量纲混掺长度l+的分布已知，就可由式（2-25）得到速度梯度的分布，积分即可得到流速分布。
在近壁区域（y/h＜0.2），混掺长度的分布可以认为是线性的。对离壁面很近、粘滞效应起决定性作用的情况可用van Driest（1956）的衰减函数描述流动。对于边界层和封闭管道内的流动来说，可以给出如下的标准分布形式（见Huffman&Bradshaw1972，Reynolds 1974），
式中：κ是Kármán常数，Г（y）是van Driest衰减函数；B是衰减系数，van Driest（1956）对边界层流动所给出的经验值为B=26。经过验证此数值也适用于明渠流（Nezu和Rodi，1986）。在不同区域利用式（2-26a）、式（2-26b）对式（2-25）积分，即得流速分布。在粘滞底层内，l+≪1，ξ≪1，有dU+=dy+，可得
在过渡区外，l+≈κy+≫1，ξ＜1，有dU+/dy+=1/κy+，所以
式中：A是积分常数。式（2-27）为粘滞底层（viscous-sublayer）速度律，式（2-28）为对数分布速度律（log-law）。两式都属于由内层变量u*和v所确定的壁面定律。应注意上面各式中的Kármán常数κ和积分常数A是根据壁面层内（y/h＜0.2）的实测资料确定的。
式（2-27）和式（2-28）的应用范围中间有一段过渡区（buffer layer，5＜y+＜30），在这一区域不能对式（2-25）作出简化。
窦国仁（1980）根据随机理论推导得到的各区统一公式如下
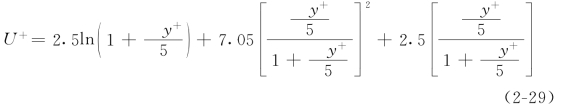
3.主流区内的流速分布规律
在明渠流动中，经常需要给出主流区内时均流速沿垂线方向（一般记为y方向）的分布。与圆管流动和封闭管道流动比较而言，明渠流动的外区（outer region，y/h＞0.2）中混掺长度的资料向来较为缺乏。Keulegan（1938）提出在明渠流动中可以假定对数流速分布沿全水深分布，这一假定在实际中一直得到广泛应用。对于各种不同情况下的流动，需要调整、率定Kármán常数κ和积分常数A，但实际上往往是不加分析直接引用Nikuradse对圆管流动所得到的常数，如水力光滑流动时的κ=0.4，A=5.5。
20世纪80年代进行的一些研究表明，对数分布速度律式（2-28）只在壁面层内成立，实测流速分布与对数分布公式之间的差别不应通过调整常数κ和A来消除，而是必须象边界层理论中那样，在式（2-28）中增加一个尾流函数（wake function）如下
尾流函数w（y/h）的形式可以采用Coles（1956）所给出的经验关系
其中∏是Coles给出的尾流强度参数。据分析，在许多边壁剪切流动中，壁面附近区域不受外部流动条件影响，边壁处流动的相似性原理应当成立，所以对数分布律中的Kármán常数κ和A应保持一个恒定值。虽然其他人也提出了不同形式的尾流函数（Sarma et al 1983，Coleman&Alonso 1983），但Coles的尾流函数仍是应用最普遍的对数律修正方法。由式（2-30）和式（2-31）就得到如下的亏值律（velocity defect law），又可称为“对数-尾流定律（log-wake law）”：(www.xing528.com)
式中：
=Umax/u*。当∏=0时，式（2-32）即为一般的对数分布公式，换句话说，Coles的尾流强度参数∏描述流动的“外区”（outer region）流速分布与对数分布的偏离程度。Cardoso et al（1989）从10组试验得到∏=0.079和κ=0.402，他们认为明渠流动可能受二次流、上游来流及不活跃紊动分量（inactive turbulence components）的影响，不存在普遍意义的尾流函数。
王殿常等（1998）比较了发展中的边界层流动和明渠流动，深入分析了将尾流律应用于边界层流动和明渠流动时存在的差别后，认为如果摩阻流速能够由水流条件（如水深、流量、均匀流的底坡）计算获得，则对于对数律有两个系数需要由测量资料确定，而尾流律则需要确定三个系数，因此边界层流动的亏值律表达式对于明渠流动没有实际意义。关于这一问题的详细论述见本书第七章。
4.时均流速的对数型分布公式
Kuelegan（1938）用实验数据确定系数后，提出了如下的二维明渠紊流中速度沿垂线分布的对数型公式（注意此处采用以10为底的常用对数）。
壁面水力光滑情况：此时粘滞底层能够覆盖壁面粗糙，可视为光滑壁面。
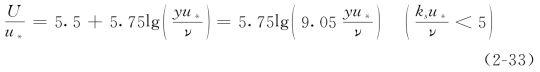
式中：U为距床面y处的时均流速，ksu*/ν=k+为无量纲粗糙高度，也称为剪切雷诺数（Shear Reynolds number）；ks为壁面粗糙突起高度（又称粗糙尺度，因其大部分情况下是一个代表性的特征值）。可见，这种情况下流速沿垂线的分布只受γ，R，J，ν的影响。
壁面水力粗糙情况：粘滞底层被扰乱，不能够覆盖壁面粗糙突起，紊流流区受糙率突起的影响，流速分布为
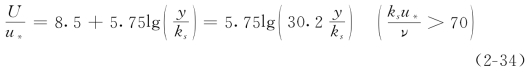
可见，此时流速沿垂线的分布除受γ，R，J的影响外，还受到边壁粗糙程度（用边壁突起高度ks表示）的影响。
Einstein的水力光滑、水力粗糙统一公式（1950）：Einstein用一个校正系数χ（水力光滑区和水力粗糙区取不同值），将Kuelegan的两个公式统一为
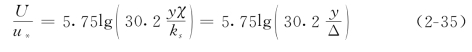
式中：Δ为表观糙率（因其在公式中的位置而得名），Δ=ks/χ；χ为校正系数，它是ks/δ的函数，其中δ=11.6ν/u*是粘性底层的计算厚度。χ与ks/δ的关系如图2-5所示。
5.其他常用经验公式
在大量实验和实测的基础上对明槽的垂线流速分布曾总结过不少纯经验公式，下面是较常见的两种。
（1）抛物线型流速分布公式
式中：Umax为水面流速；m为常数，其值约为20～24。该式是根据大型水槽试验资料得到的，应用得较为普遍。用该式计算起伏较大的河床的平均河底（y=0）处的流速值可以得到一定值，而前述对数流速分布公式不能用于y=0的位置。
（2）指数型流速分布公式
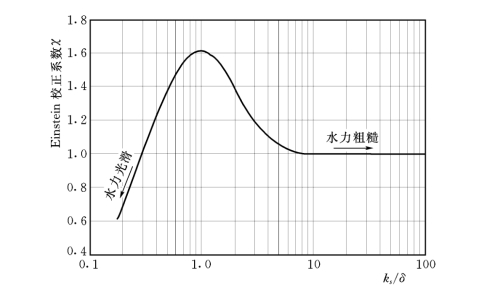
图2-5 Einstein校正系数χ与ks/δ的关系
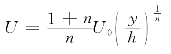
式中：n是与河流特性有关的常数，一般为5～9；U0为垂线平均流速。该式结构简单，由试验证明有一定精度。
6.粗糙高度的表示方法及理论床面的确定
用均匀颗粒加糙的床面，壁面粗糙是均匀的，粗糙高度等于颗粒粒径，用符号ks表示。它属于内层变量，无量纲形式为
=ks/（ν/u*）。按照
的大小，可以对壁面粗糙的效应作如下分类：
若床面是水力光滑的，则壁面粗糙对流动的效应会消失。若床面是完全粗糙的，则粘滞底层对流动的效应会消失，因为粗糙凸起已经进入紊流的对数流速分布区域。部分粗糙床面上，壁面粗糙和粘滞底层对流动的效应都会存在。
对于光滑床面来说，垂线流速分布的原点就位于床面上，此处y=0，U（0）=0。对于水力光滑的情况，粘滞底层存在，对数分布只能用于粘滞底层以上的部位，所以不可将y=0代入对数型的流速分布公式（代入后所得的值无物理意义）。当床面属于完全粗糙时，理论上的平均床面并不是粗糙突起的最高点所在平面，而应取最高点所在平面以下一定距离处，这样计算出的对数型流速分布才能与实测结果符合。Einstein和El-Samni（1949）在床面上铺半圆球的研究表明，以圆球顶点平面作为理论床面计算y点绘的U～lg（y）关系为一曲线，而以圆球顶点平面以下0.2D（D为圆球直径）的床面作为理论床面计算y时，点绘的U～lg（y）关系为一直线。此时，在y=0～0.2D这一范围内应用对数分布公式也是无意义的，因为此范围内的边界条件及紊动状况可能已经超出了公式所能够应用的范围。Grass（1971）也提出以圆球顶点平面以下δ为理论床面（图2-6），且δ/ks=0.18，Nakagawa et al（1975）则提出δ/ks=0.25。对于沙粒加糙的床面来说，大致有δ/ks=0.15～0.3。
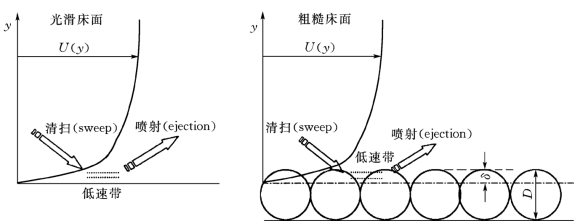
图2-6 光滑床面与粗糙床面上的流速分布理论床面
卞华等（1998）采用二维激光流速仪对二维加糙明渠紊流进行的试验表明，理论基面位置主要受糙元间距的影响，若以λ表示糙元中心距，ks表示粗糙高度，则当λ/ks=2，4和λ/ks≥8时求得的理论基面分别在粗糙突起顶点平面以下0.3ks，0.5ks和1.0ks。不同糙元形状对理论基面的影响不大。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
