河流动力学中常用的紊流基本方程,是以粘性不可压缩流体的连续方程和运动方程为基础推导得到的。
(1)连续方程和运动(N-S)方程。从不可压缩流体的质量守恒可以得出其连续方程
![]()
对不可压缩的运动流体进行力学分析可以得出N-S方程
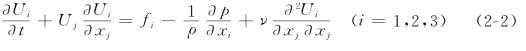
式中:Ui为i(i=1,2,3)方向的瞬时流速,同一项中下标相同即为三项相加,如式(2-1);p为瞬时压强;fi为单位质量上的体积力。
(2)时均Reynolds方程与Reynolds应力。在圆管或其他时均流线为平行的紊流流动中,在垂直于时均流动的方向上有不规则的流速脉动(即流动是三维的),所以不能把N-S方程简化为二维后求解此类流动,否则求出的仅是层流解。Reynolds对N-S方程进行了时间平均的处理,以求消除时均值为零的脉动流速在方程中的存在,然而却出现了新的变量—Reynolds应力,即动量交换而形成的表观应力(apparent stress)。没有流速梯度(迁移加速度)的流场中,不存在Reynolds应力,换言之,它只在剪切紊流中存在。
由N-S方程出发推导Reynolds方程时,首先定义时间平均流速为
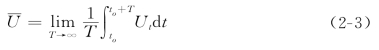
式中:T→∞表示积分时段与紊流脉动周期相比足够大。在非恒定流中,T相对于宏观物理量的变化周期仍取为有限时段,从而使宏观物理量时均值仍随时间变化。
再将瞬时流速Ut分解为时均流速![]() 与脉动流速u之和
与脉动流速u之和
![]()
其中脉动值的时均为零
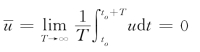
两个瞬时流速乘积的时均为

对N-S方程进行时均计算,得Reynolds方程为(其中Ui为时均流速,P为时均动水压强)
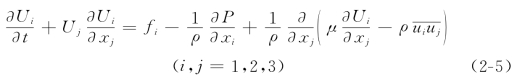
式中:![]() 的物理意义是剪切紊流中紊动引起的相邻流层间的动量交换,表现为相邻流层间的切应力,称之为Reynolds应力(Reynolds stresses)。
的物理意义是剪切紊流中紊动引起的相邻流层间的动量交换,表现为相邻流层间的切应力,称之为Reynolds应力(Reynolds stresses)。
(3)Reynolds方程组封闭问题。Reynolds应力的出现使Reynolds方程组比N-S方程组增加了6个独立未知量,但方程组中方程的个数并未增加(仍为三个运动方程和一个连续方程),这样未知量个数多于方程个数,从而引起Reynolds方程组不封闭,称之为Reynolds方程组封闭问题(closure problem of the Reynolds equation system)。解决封闭问题主要采用两个方法:一是减少变量个数,在方程组中消去多余变量![]() ;二是增加方程个数。
;二是增加方程个数。
(4)明渠二维紊流的基本方程。恒定、均匀明渠流动有较大的宽深比时,可以按二维流动处理。在图2-2所示的二维流动中,大写符号U,V,W分别表示时均流速在流向、垂向和横向上的分量,小写符号u,v,w分别表示脉动流速在流向、垂向和横向上的分量(小写符号左上角加一撇u′,v′,w′则分别表示脉动流速在流向、垂向和横向上分量的均方根值)。
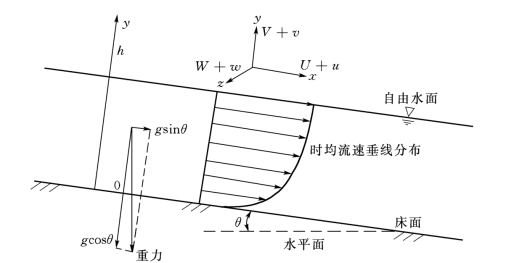
图2-2 明渠二维流动示意图(https://www.xing528.com)
在恒定不可压缩二维明渠流动中,连续方程和Reynolds方程的形式为
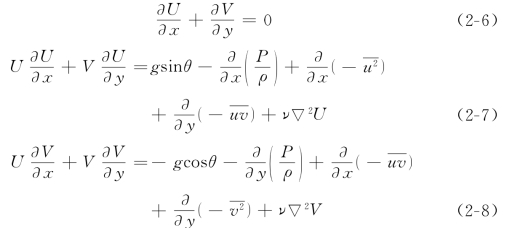
式中:P为时均动水压强;ρ为流体密度;g为重力加速度;ν为运动粘滞系数;θ为渠底与水平面的夹角;符号▽为Hamilton算子,(▽=i∂/∂x+j∂/∂y+k∂/∂z);▽2为Laplace算子,(▽2=∂2/∂x2+∂2/∂y2+∂2/∂z2)。在均匀明渠流动中,V=0,∂/∂x=0,式(2-8)在y方向上从点y积分到水面y=h处可得
![]()
式中:![]() 是水面处垂向流速脉动的均方值,由于自由水面的存在使得
是水面处垂向流速脉动的均方值,由于自由水面的存在使得![]() =0。右边第一项是静水压强,第二项则表示由于脉动流速的存在所引起时均动水压强P/ρ与静水压强之差。
=0。右边第一项是静水压强,第二项则表示由于脉动流速的存在所引起时均动水压强P/ρ与静水压强之差。
将条件V=0,∂/∂x=0代入式(2-7),积分后与式(2-9)联合得到

式中:u*是摩阻流速;J是能坡,J≡τ0/(ρgh)。水面坡降为JS≡sinθ—cosθdh/dx,此处J=JS。式(2-10)表明垂线上的剪切应力随水深呈线性变化,从床面处的τB减少至水面的零。
在二维均匀流动中,(∂U/∂y)是变形率,乘以Reynolds应力即为该应力所作的变形功(deformation work)。紊动动能的生成率G和时均流能量的直接耗散率E定义如下

这两者都消耗时均流动的能量。将式(2-10)两边乘以(∂U/∂y)并从y=0积分至y=h,可以得到下式

式中:Um是总流平均流速(即全断面平均,在此处的二维均匀流动中为垂线平均)。上式右边的(τb/ρ)Um一项为剪切应力与流速的乘积,即时均流动克服床面剪切力所耗费的功率。式(2-14)表明时均流动的机械能损失有两个原因,就是紊动动能的生成和时均流动能量的直接粘性耗散,如图2-3所示。紊动是时均流动机械能转化为流体微团紊动动能,粘性耗散则是时均流动机械能和紊动动能转化为分子热运动。
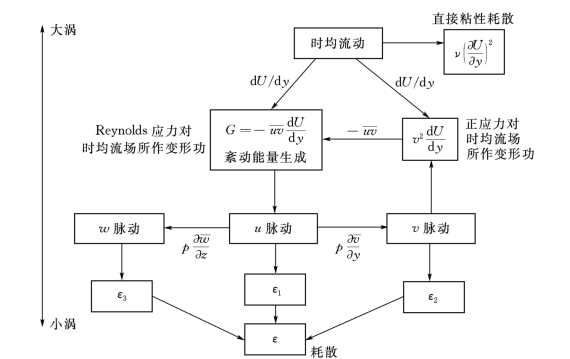
图2-3 紊动动能从生成到耗散的输运过程(引自Nezu和Nakagaw a,1993)
文献中“eddy”一词一般指紊流中出现的带随机性质的旋转流体团,中文译为“涡旋”;而“vortex”一词是指理想流体的有旋流动或粘性流体的层流流动中出现的确定性旋转流体团,中文译为‘旋涡’。紊动脉动能量的生成G主要与大尺度的涡旋有关。大涡又会将其紊动能量通过一系列破碎过程传给较小的涡旋,形成一种梯级传递过程,最终这些紊动能量在小涡的尺度上由分子粘性耗散为热运动,造成时均流动机械能(mechanical energy)的减少。随着Reynolds数的增加,时均能量的直接耗散仅在边壁附近才较为显著。一般来说,正应力对时均流场所作变形功与切应力相比要小得多(参见夏震寰1992,134页)。工程计算中常用的二维流动控制方程是把三维方程沿水深平均后、把摩擦阻力用代数方程(如Chezy公式)概化后所得到的,一般称为浅水方程或二维Saint-Venant方程,用于研究在各种作用力影响下xoz平面区域内水流的运动,应注意不要把它与本节所说的xoy平面上的恒定不可压缩二维明渠流动方程式(2-7)、式(2-8)相混淆。若只需研究一维明渠流动,即对水力要素在横断面上取平均,则常用一维Saint-Venant方程。
(5)二维明渠紊流的脉动能量方程。二维明渠充分发展紊流的脉动能量方程为

式中:p是压强脉动;εi是各流速分量相应的紊动耗散率。对于明渠二维剪切流动,紊动的产生项G只在u分量方程中出现,这就是为什么实测中有u′>v′,u′>w′。各分量方程中左边第一项是压强-应变相关,正是通过这一作用使得紊动能量从u′重新分布到v′和w′。压强脉动的作用就是使紊流变得趋向于各向同性化。鉴于压强-应变相关项在紊动能量重新分布过程中所起的重要作用,在精细的紊流模型中必须将其包括在内,以准确地计算u′,v′和w′的分布。将方程式(2-15)~(2-17)相加,由连续方程可消去其中的压强-应变相关项,得到紊动动能k(≡u′2+v′2+w′2)的控制方程如下
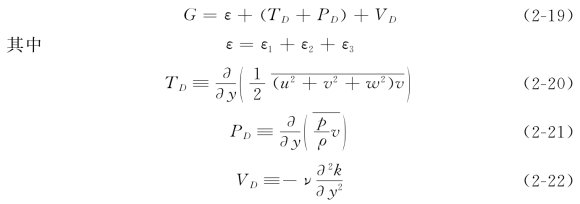
对于Reynolds数较高的流动,粘性扩散项VD在离边壁稍远处即可忽略,但在粘性底层中它起着重要作用,在较高Reynolds数下也不能忽略。紊动扩散项有两个,一个是紊动引起的能量扩散TD,一个是压强脉动引起的能量扩散PD。ε是总耗散项,其紊动能量耗散过程见图2-3。小尺度涡旋的性质趋向于各向同性,因此可以写出如下表达式(详细推导参见Hinze 1975,219页)
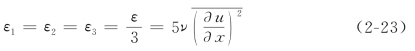
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




