梯形蜗壳的圆角设计优化

前面的计算是在梯形截面的顶角都为锐角的情况下进行的。这种顶端的锐角无论是对蜗壳的铸造工艺还是气流的流动方面都是不利的。因此，在一般离心压缩机中，都把顶角倒成半径为R的圆角。

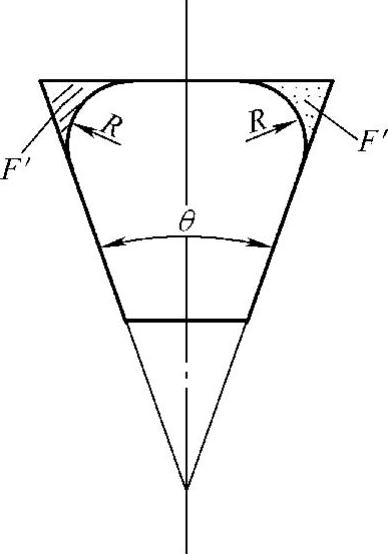
图4-24 梯形蜗壳顶角的倒圆角

如图4-24所示，倒成圆角后，每个圆角将使蜗壳截面减少面积为

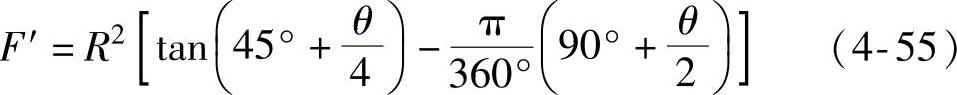
式中 F′——把蜗壳顶角倒圆后，每个圆角使蜗壳减少的面积；

R——圆角半径。

每个圆角所减少的面积一般可取为F′=K_rF_φ，K_r为圆角截面积修正值，K_r=0.03～0.07。

按式（4-56）可得梯形顶角倒圆的半径R为

式中 F_φ——正梯形面积。

由于上述倒圆角的影响，会使蜗壳截面系数J和截面积F_φ下降，为了抵消这种影响，可大致采用下列方法进行弥补。

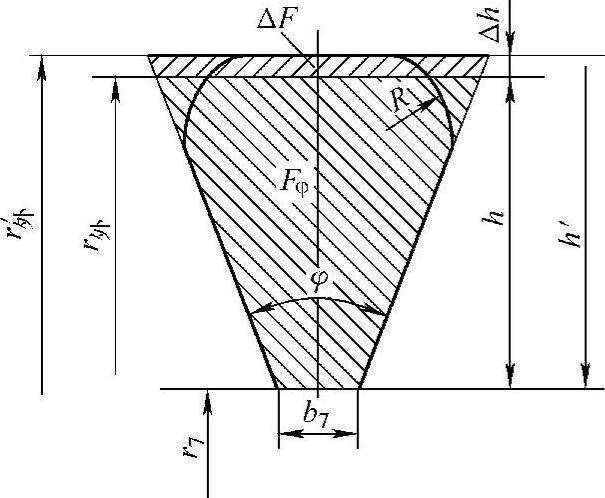
图4-25 蜗壳高度的修正

如图4-25所示，可以把梯形高度h增大到h′（即计算外半径r_外增大到r′_外），使梯形面积由F_φ增大到F′_φ，截面积的增加量ΔF_φ为

ΔF_φ=F′_φ-F_φ=2F′

梯形面积F为

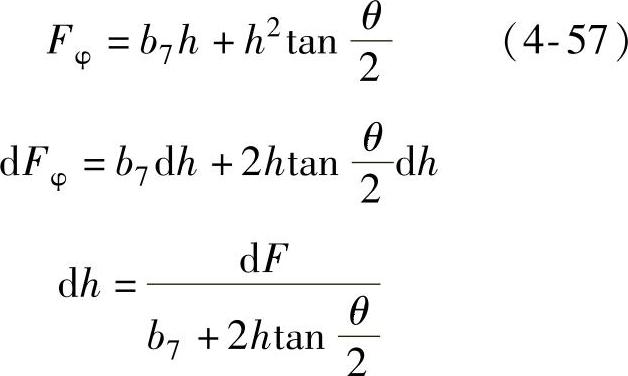
蜗壳高度修正值Δh为

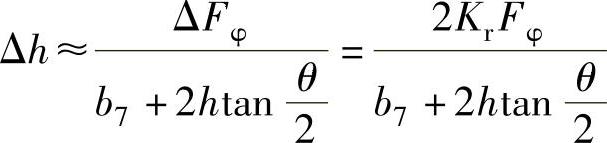
修正后的蜗壳高度为

式中 h——修正前的正梯形蜗壳截面高度，h=h_外-r₇；

h′——修正后的蜗壳截面高度；

F_φ——修正前的正梯形截面面积；

θ——蜗壳截面扩张角；

b₇——蜗壳进口宽度；

r₇——蜗壳进口半径。

为了改善气体在蜗壳内的流动，对于不带扩压器的蜗壳，其蜗壳扩张角θ应不超过45°；对于带有扩压器的蜗壳，扩张角θ可以允许增大到50°～60°。

为了减少蜗壳舌尖厚度对气流的影响，如图4-26所示，一般把舌尖的位置角φ₀移在φ₀=25°～30°（一般采用φ₀=22°30′较多）。(https://www.xing528.com)

蜗壳进口直径D₇的取值方法如下：

a.D₇＞D₄，带扩压器的蜗壳。

b.D₇=（1.03～1.15）D₂，不带扩压器的蜗壳。

c.蜗壳进口宽度为b₇。b₇≈b₄，不带叶片扩压器的蜗壳；b₇=（1.5～1.6）b₄，带叶片扩压器的蜗壳；b₇=（1.4～1.7）b₂，不带扩压器的蜗壳。

在蜗壳之后，为了降低气流速度、提高气体压力，可采用如图4-26所示的扩压管道，使气流速度能下降到20～40m/s。

扩压管道的当量扩压角θ一般可取θ=8°～12°。

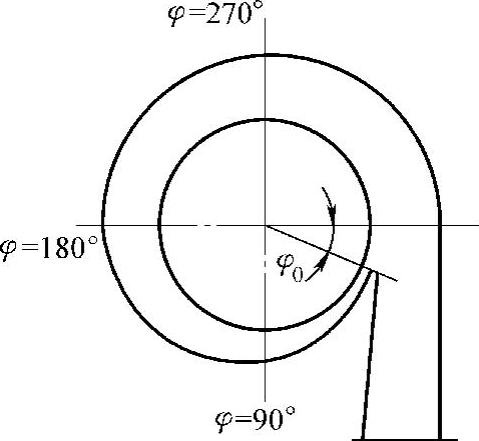
图4-26 蜗壳末端的扩压管道

[例题4-5] DA350-61型压缩机第三段蜗壳尺寸。蜗壳为不带扩压器的梯形截面结构。

已知：叶轮直径D₂=528mm；叶轮出口叶片宽度b₂=24mm；叶轮出口周速c_2u=123.2m/s；体积流量q_Vj=1.436m³/s；蜗壳出口比容比k_V0=1.406；叶轮出口比容比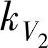=1.352；蜗壳平均比容比k_V=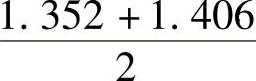=1.379。

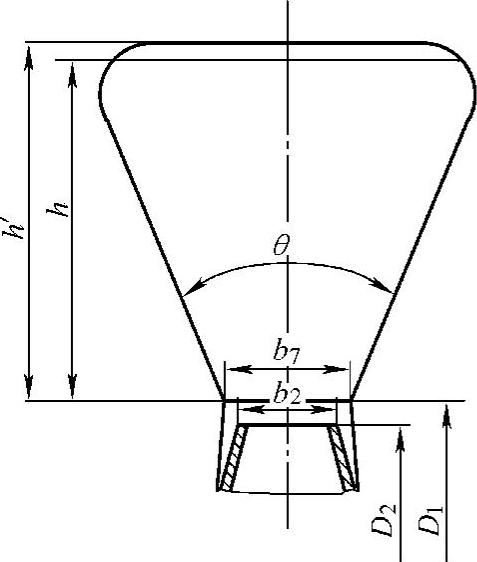
图4-27 蜗壳计算

解 取蜗壳进口宽度b₇=1.67b₂=1.67×24mm=40mm，蜗壳进口直径D₇=1.06D₂=1.06×528mm=560mm，蜗壳扩张角θ=45°，动量矩修正系数K_S无扩=1.15，圆角修正值K_r=0.05。

按照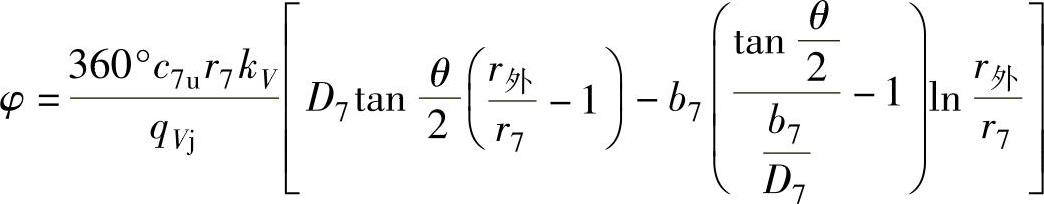

由表4-1求出正梯形蜗壳外径r_外与蜗壳截面位置角φ的关系。

其中，=560mm×0.4142=232mm，

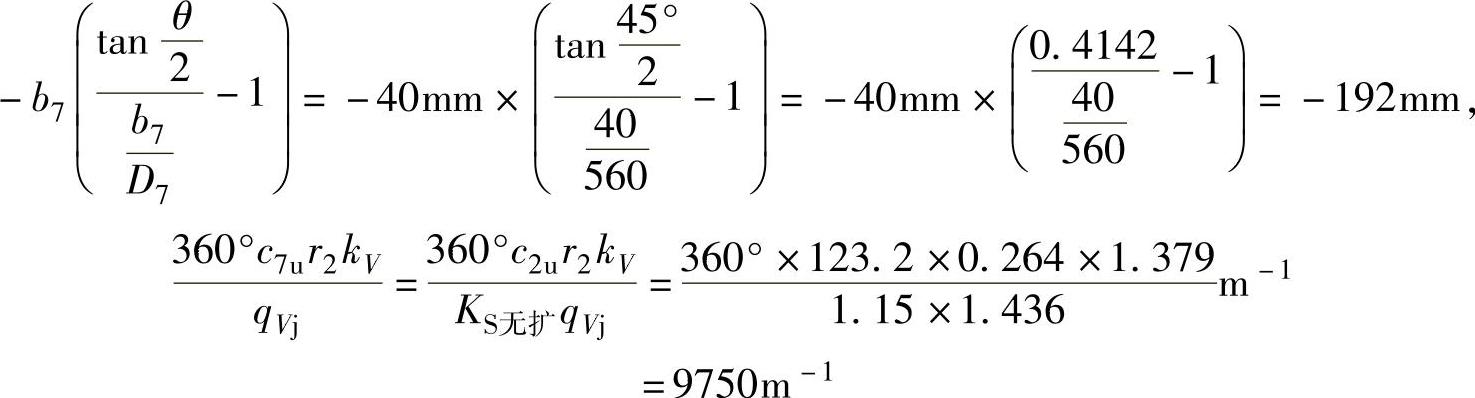
注：按式（4-46）计算时，应统一以m为单位。

表4-1 蜗壳外径与蜗壳截面角关系

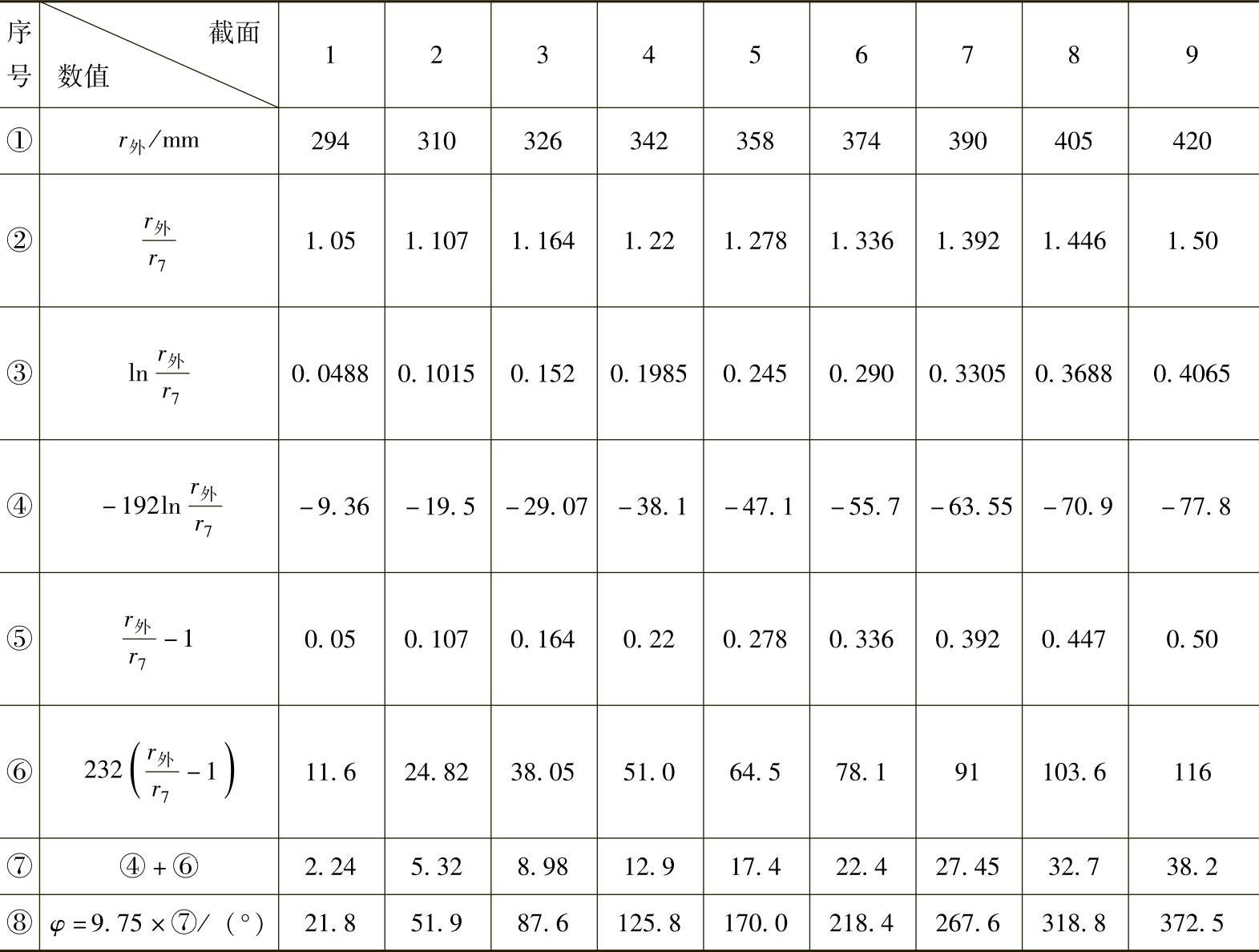
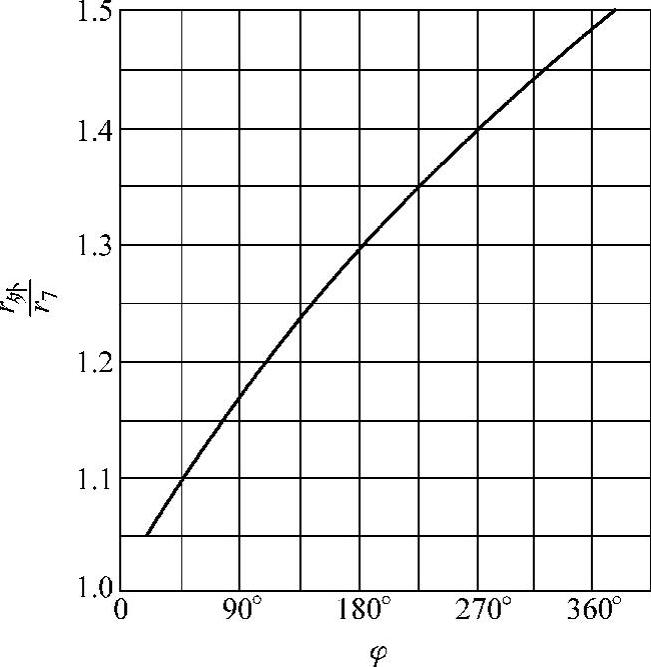
图4-28 蜗壳半径比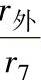与位置角φ的关系[例4-5]

由表4-1的结果绘出半径比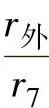与位置角φ的关系曲线，如图4-28所示。可从曲线上找出φ=22.5°、45°、…等时的半径比。

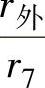现在可按下列公式用列表的方法求出各位置角φ截面的蜗壳截面面积F_φ、圆角半径R和修正后的蜗壳高度h′等。

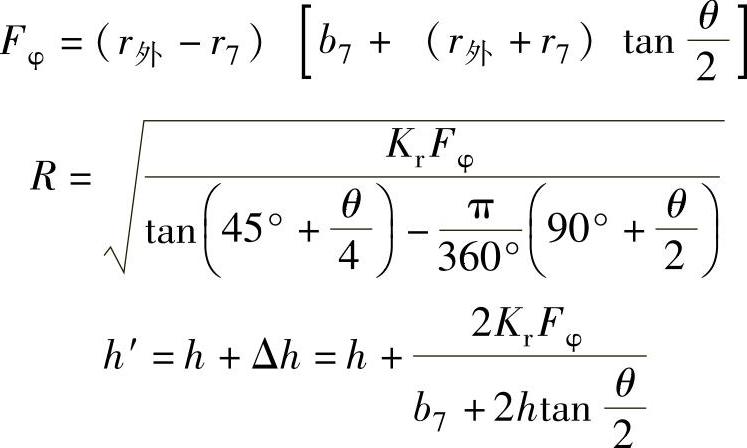
其中，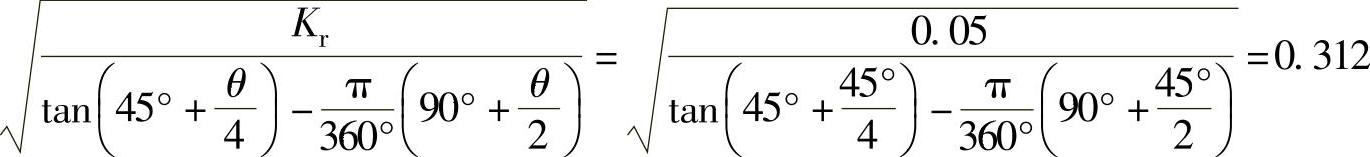

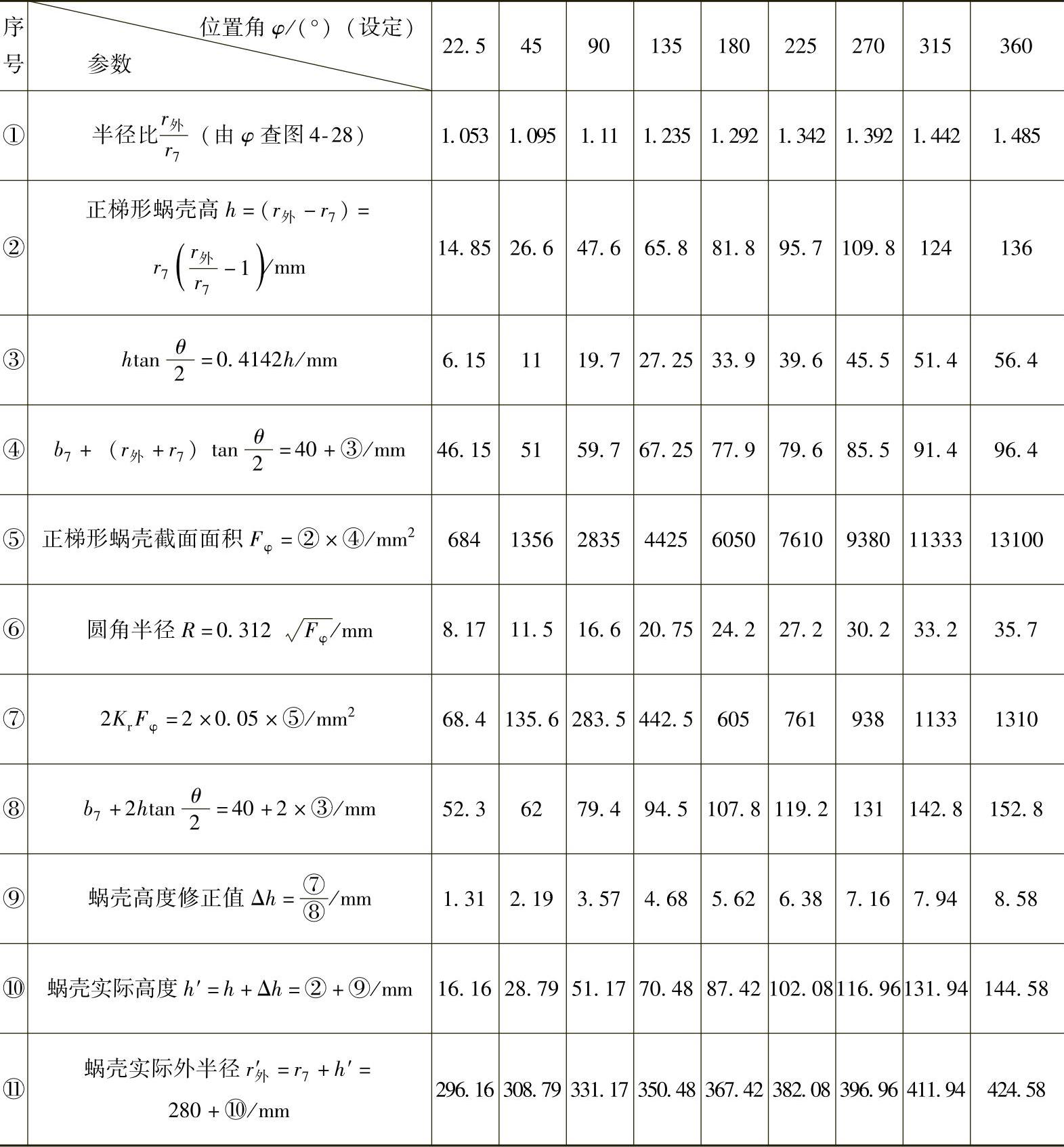
表4-2为计算数据及梯形蜗壳的计算结果。

表4-2 计算数据及计算结果