蜗壳截面计算方法与应用

1）蜗壳截面系数J和截面面积F的基本计算方法。

对于任何复杂形式的蜗壳截面系数J和截面面积F，都可以用图4-20所示的作图法，把蜗壳截面切成很多细窄的条状面积进行计算。

也可用积分的方法进行计算：

2）梯形蜗壳截面系数J的计算。

图4-21所示为梯形蜗壳截面的参数，蜗壳的内半径r_内=r₇。梯形截面在任意半径r上的宽度b为

式中 θ——蜗壳截面的扩张角（°）；

b₇——蜗壳进口宽度；

r₇——蜗壳进口半径。

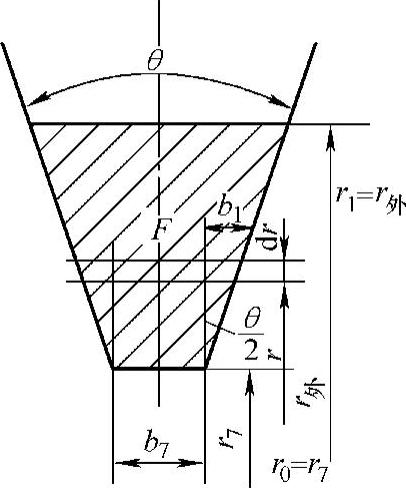
图4-21 正梯形蜗壳

梯形蜗壳的截面系数J为

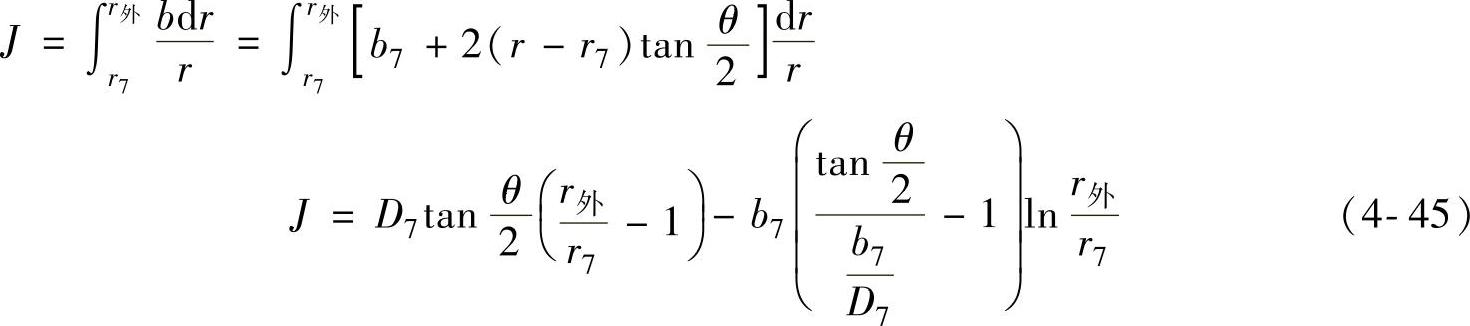
现在可以利用式（4-41）与式（4-45）的关系，找出在梯形蜗壳截面的蜗壳外径r_外与蜗壳位置角φ之间的关系为

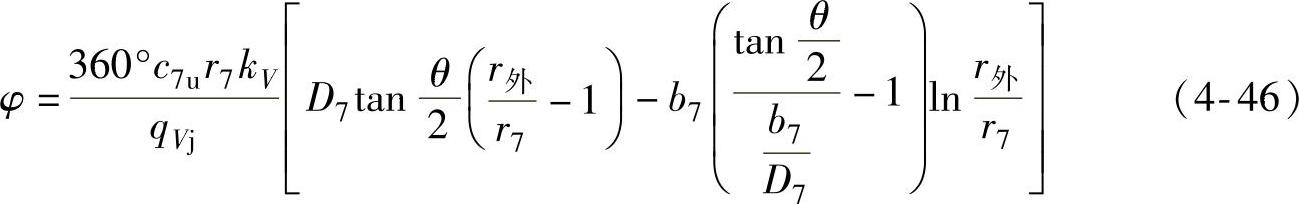
3）圆形蜗壳截面系数J的计算。

图4-22所示为圆形蜗壳的两种形式，图4-22a所示为外径不变的内涡式圆形蜗壳，图4-22b所示为内径不变的外涡式圆形蜗壳。

任何形式的圆形蜗壳的截面系数J可表示为

式中 ρ——圆截面的截面半径；

R_c——蜗壳圆形截面的圆心半径位置；

r——计算半径；

b——圆截面在计算半径r处的宽度，有

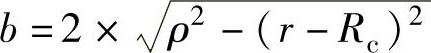
可得圆形蜗壳的截面系数J为

(www.xing528.com)

蜗壳截面尺寸与位置角φ（°）的关系为

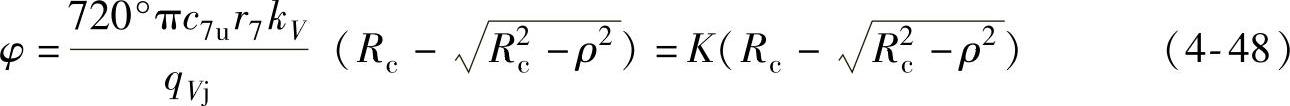
其中，K=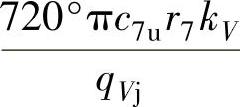[（°）/m]；qVj为段的进气体积流量（m3/s）。

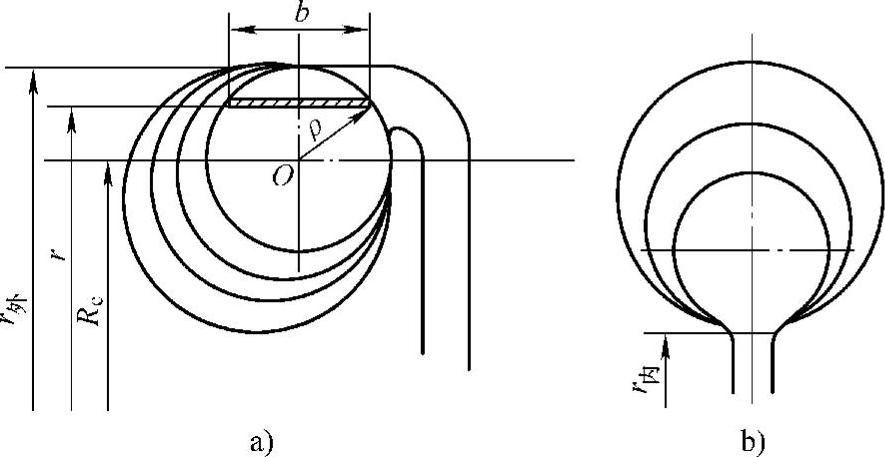
图4-22 圆形蜗壳

a）内涡式圆形蜗壳 b）外涡式圆形蜗壳

下面介绍不同圆形蜗壳的截面计算。

①外径不变的内涡式圆形蜗壳。由于r_外=定值，则R_c=r_外-ρ。

可得任意位置角φ时的蜗壳圆截面半径ρ（m）为

②内径不变的外涡式圆形蜗壳。由于r_内=r₇=定值，则R_c=r₇+ρ。

可得任意位置角φ时的蜗壳圆截面半径ρ（m）为

③中径不变的圆形蜗壳。由于R_c=r₇=定值，可得任意位置角φ时的蜗壳圆截面半径ρ（m）为

4）矩形蜗壳截面系数。

矩形蜗壳截面系数可表示为

式中 b——矩形蜗壳的宽度为定值（m）。

由此可得蜗壳位置角φ与截面参数的关系为

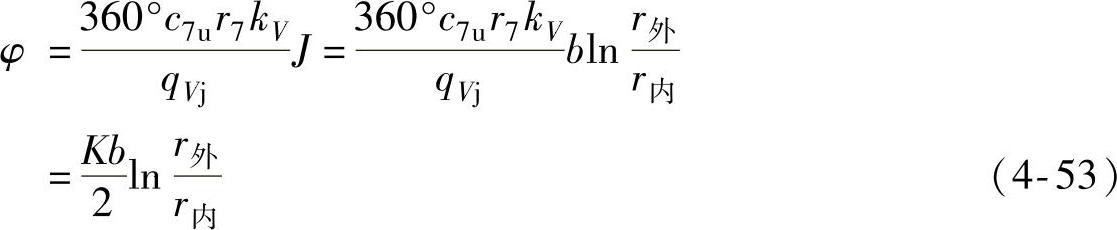
其中，K=。

在外径r_外为定值的情况下（图4-23），不同位置角φ的蜗壳内径r_内可表示为

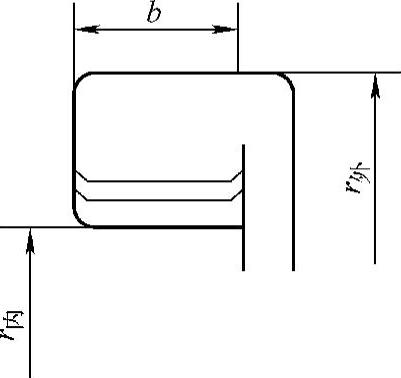
图4-23 矩形蜗壳