蜗壳设计方法：掌握气流流动规律与截面系数J的重要性

为了能够掌握蜗壳的设计方法，首先来讨论气流在蜗壳中的两个基本流动规律。

1）蜗壳任意截面上的体积流量q_Vφ与位置角φ成正比。在设计工况时，叶轮的出口气流是沿圆周均匀分布的。因此，在不同位置角φ截面上的流量q_Vφ可表示为

式中 φ——截面位置角（°）；

k_V——蜗壳中的气体平均比容比。

2）气流的动量矩不变（c_ur=常数）的规律流动。气体在蜗壳里的流动，与气体在无叶扩压器中的流动相似。在忽略流动阻力的情况下，按照动量矩不变的原理，气流的圆周分速度c_u将随着流动半径r的变化而成反比地变化，所以

其中，r₇和c_7u分别表示了图4-18所示的蜗壳进口7-7截面上的半径和气流圆周分速度。

对于带有无叶扩压器的蜗壳来说，考虑到流道中的流动阻力等的影响，蜗壳里的气流圆周分速度可表示为

蜗壳任意点的圆周分速度c_u为

蜗壳进口截面的圆周分速度c_7u为

式中 K_S无扩——动量矩修正系数，K_S无扩=1.1～1.2；对于外涡式蜗壳，一般可取K_S无扩=1.15；对于内涡式蜗壳，则可把修正系数取得大一些。

对于带有叶片扩压器的蜗壳，蜗壳内的气流圆周分速度可表示为

蜗壳任意点的圆周分速度c_u为

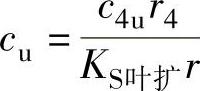
蜗壳进口截面的圆周分速度c_7u为

式中 K_S叶扩——动量矩修正系数，K_S叶扩=0.80～0.85；

c_4u——以叶片安装角α_4A作为气流的出口角方向，计算所得的叶片出口前的气流圆周分速度。

由于扩压器叶片数是有限的，通过扩压器叶片的气流方向，不可能完全按照叶片出口安装角α_4A流出去。与无叶扩压器中的气流相似，在叶片扩压器中，气流本身也具有按照对数螺旋线流动的趋势，在这种趋势的影响下，实际气流流出叶片后的方向角α′₄要比叶片出口安装角α_4A小，实际气流流出叶片后的气流圆周分速度c′_4u要比c_4u大。因此，带叶片扩压器的蜗壳计算中的动量矩修正系数K_S叶扩要取得比带无叶扩压器的蜗壳小。(www.xing528.com)

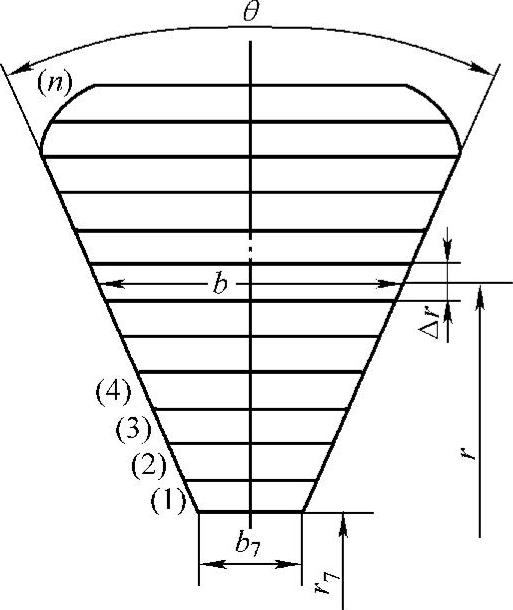
图4-20 蜗壳截面积的计算

把整个截面看做图4-20所示的由很多细窄的截面组成，每一条细窄的截面积为ΔF，有

ΔF=bΔr

式中 b——细窄截面的平均宽度；

Δr——细窄截面的高度，每一条细窄截面上的流量为q，有

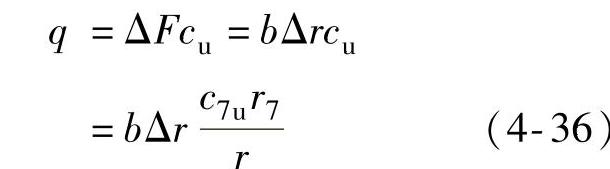
b=f（r）

式中 c_u——细窄截面的气流平均圆周分速度；

r——细窄截面的平均半径；

r₇——蜗壳进口半径；

c_u7——蜗壳气流进口圆周分速度。

整个蜗壳截面上的流量为

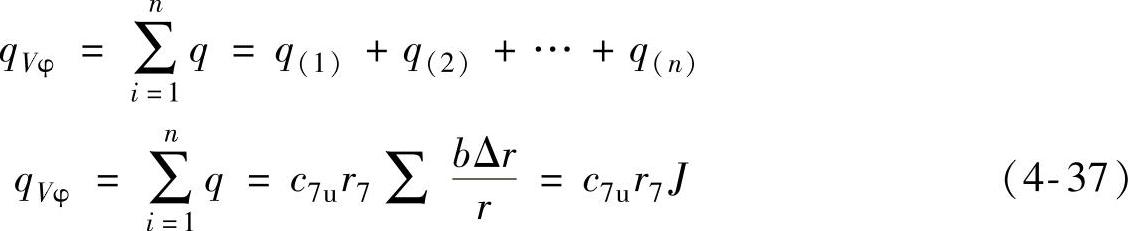
式中 J——蜗壳截面系数（m），

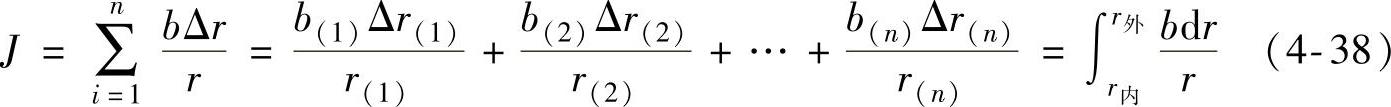
或表示为

由式（4-37）可以看出，在蜗壳进口半径r₇及圆周分速度c_7u一定的条件下，蜗壳截面的气流通流量与蜗壳截面系数J成正比。而气流在蜗壳不同位置角φ的通流量是不同的，由式（4-32）可知，不同位置角截面的气流量大小与位置角φ成正比。因此，把式（4-32）和式（4-37）的关系联在一起，就可以在级的体积流量、蜗壳进口半径r₇及气流进口圆周分速度c_7u一定的条件下，找出不同位置角φ上所需要的蜗壳截面系数J的大小，或者按照J的大小找出它所能适应的蜗壳位置的φ（°）。

到现在为止，可以按照式（4-40）求出不同位置角φ上所需要的蜗壳截面系数J=的大小。而截面系数J对于下一步确定蜗壳截面的几何尺寸是十分重要的。