离心压缩机级的性能曲线介绍

为了把压缩机级的特性反映出来，常常把不同流量时的级压力比（或出口压力）与流量的关系，以及效率与流量的关系，用曲线形式表示出来，称为级的性能曲线。图2-11所示为一个离心压缩机级，通过级的试验测量而得到的级性能曲线。试验是在叶轮的圆周速度u₂=270m/s时进行的，级的设计点效率η_db=0.81；设计点的级压力比ε=1.54；设计点的流量为。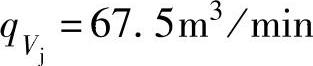

我们有必要讨论一下，形成这种级压力比和级效率曲线的原因，以便对压缩机级的性能有更深刻的了解。

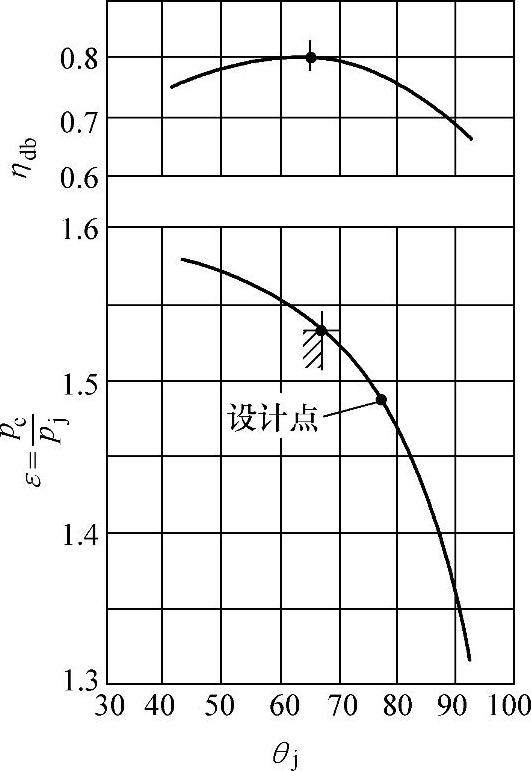
图2-11 压缩机级的性能曲线

由于级的压力比主要是由叶轮的叶片功决定的，因此，要了解压力比与流量的关系，得首先讨论叶片功与流量的关系。级的叶片功的大小可由式（2-6）表示为

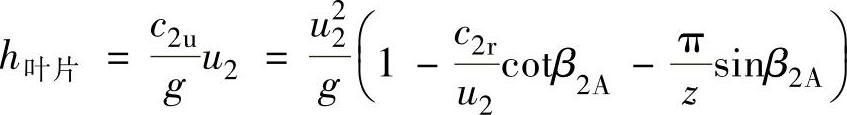
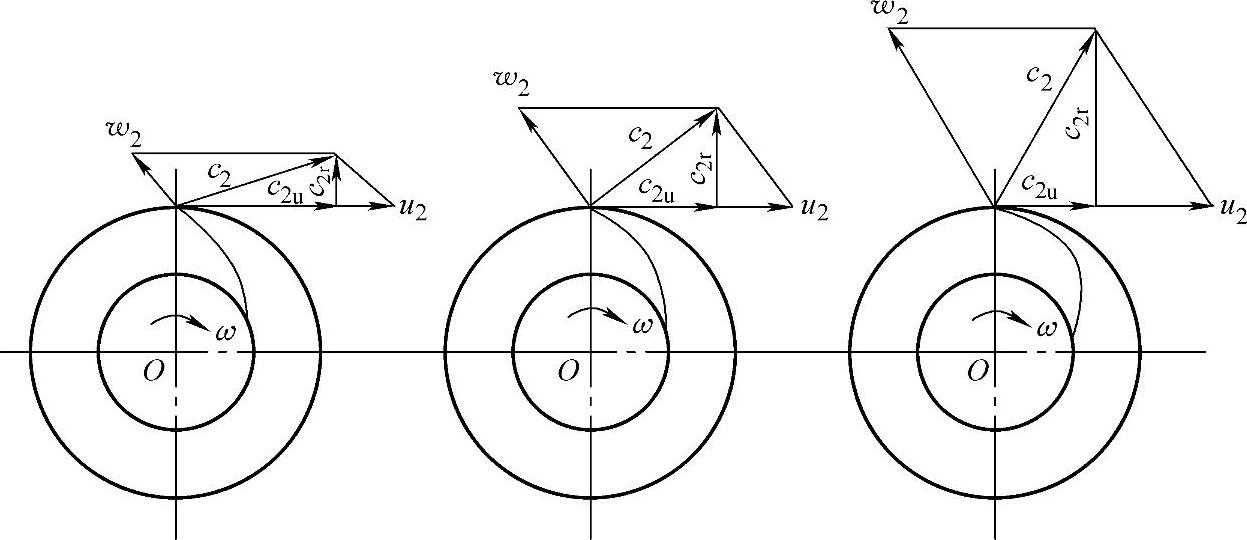
由图2-12所示的出口速度三角形开始讨论，在一般后弯式叶轮圆周速度u₂以及叶轮叶片出口安装角β_2A一定的情况下，随着级的进气流量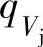的增加，叶轮出口相对速度w₂和径向分速度c_2r也随之变大。这时，叶轮出口绝对速度的圆周分速度c_2u将随着流量的增大而减小。从式（2-6）的关系可以看出，叶轮的叶片功h_叶片随流量增大（即φ_2r=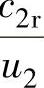增大）而降低。因此，如图2-13所示，压缩机的叶片功h_叶片将随级的流量的增加而减少。

在上一节中已经讨论过叶片功h_叶片主要是由多变功h_db和流动损失Δh_流动两部分组成，因此，要找出对级压力升高实际有效的功——多变功h_db，就应该先分析一下流动损失Δh_流动在不同流量时的情况。

对于流动损失Δh_流动，可以认为它是由流道的内部流动损失（即摩擦损失和局部损失）和冲击损失（即气流进入叶轮叶片、扩压器、回流器叶片等，由于进口部分的冲击和气流方向与叶片方向不一致所引起的损失）组成的。内部流动损失具有随着流量的增大成二次方增大的特点；而冲击损失，则在设计流量时，由于气流方向基本上与流道的叶片方向一致，相对来说，这时的冲击损失最小。然而随着流量与设计流量的偏差越大（包括流量偏大和偏小），它都会使气流方向β₁与叶片安装角β_1A的偏差变大，如图2-14所示。这种偏差的变大，都会引起冲击损失的急剧增加。

按照下列关系为

可把级的多变功h_db与流量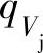的关系表示为图2-13所示的形式。由于级的压力比ε大致与多变功h_db成正比，因此图2-13所示的级压力比ε与流量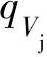的关系曲线的

(www.xing528.com)

图2-12 叶轮气流出口速度的圆周分速度c_2u与流量的关系

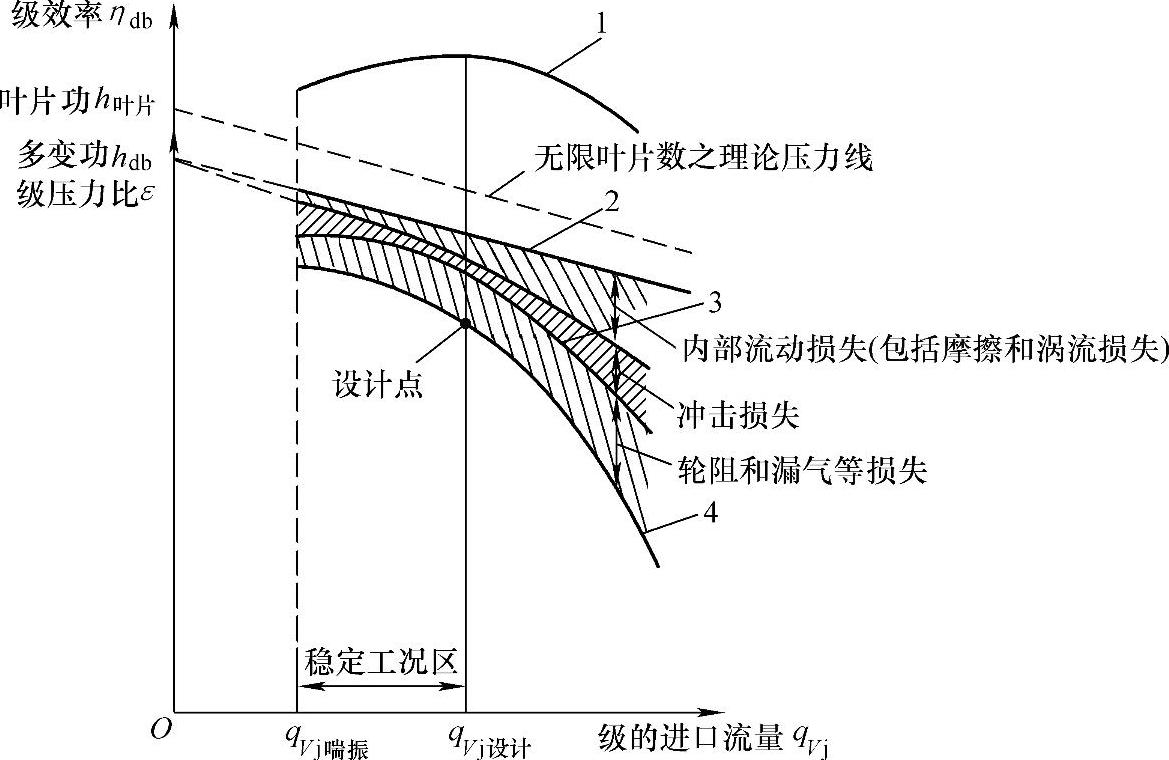
图2-13 级的性能曲线分析

1—级效率η_db曲线 2—叶片功h_叶片曲线（有限叶片数的理论压力线） 3—多变功h_db曲线 4—级压力比ε曲线（实际压力曲线）

形状基本上与多变功h_db与流量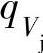的关系曲线相似。

关于级效率_ηdb的问题，一般来说在设计流量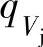时，级的流动情况比较好，它具有最高的效率。而随着流量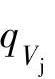的增大，由于内部流动损失Δh_内部流动和冲击损失Δh_冲击都增大得较快，使级效率在流量大时下降；在流量小于设计流量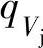的情况下一方面是由于冲击损失的增加，另一方面是由于有效流量的减少使相对的漏气损失和轮阻损失增加，也使级的效率η_db下降。这也就是使级效率曲线出现图2-13所示的中间高两头低的一般形状。压缩机级的性能曲线除反映级的压力-流量、效率-流量的关系外，同时也反映了级的稳定工作范围。压缩机级在流量减小到一定程度时，由于轴向旋涡等的影响，造成叶道里的速度很不均匀并出现倒流，这样就很容易使流道里的气流引起严重的脱离现象，使级的压力突然下降。这时，级后或压缩机后的压力气体就会出现倒流到叶轮中的现象，使级或压缩机喘振而无法工作。

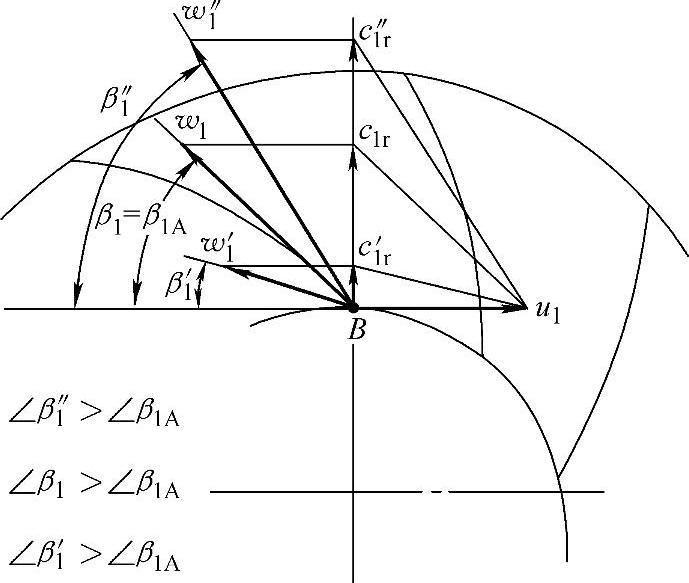
图2-14 在不同流量时的进口气流角度β₁与叶片安装角β_1A的偏差

为了说明压缩机级的工作稳定情况，通常只要指出设计流量到喘振流量范围即可，把设计流量到喘振流量的范围称为稳定工作区，并以的比值表示。对于不同叶片出口安装角β_2A的叶轮来说，β_2A越大叶轮流道中的气流速度越容易出现不均匀现象，越容易引起喘振。因而，它的稳定工作区的比值就比较小。

在圆周速度相同的条件下，为了便于级与级之间的性能比较，还常常采用能量头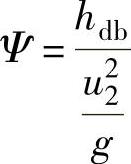系数、流量系数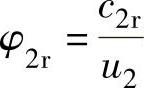和级效率η_db来表示级的性能参数。由于当圆周速度u₂一定时，能量头系数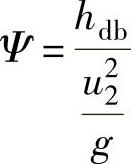与多变功h_db成正比；流量系数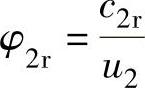基本上也与流量成正比。因此，如图2-15所示，用能量头系数Ψ、流量系数φ_2r和多变效率η_db表示的级性能曲线，其形状与用流量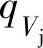、多变功h_db和多变效率η_db为坐标的曲线是基本相似的。这时的稳定工作值的比值为。

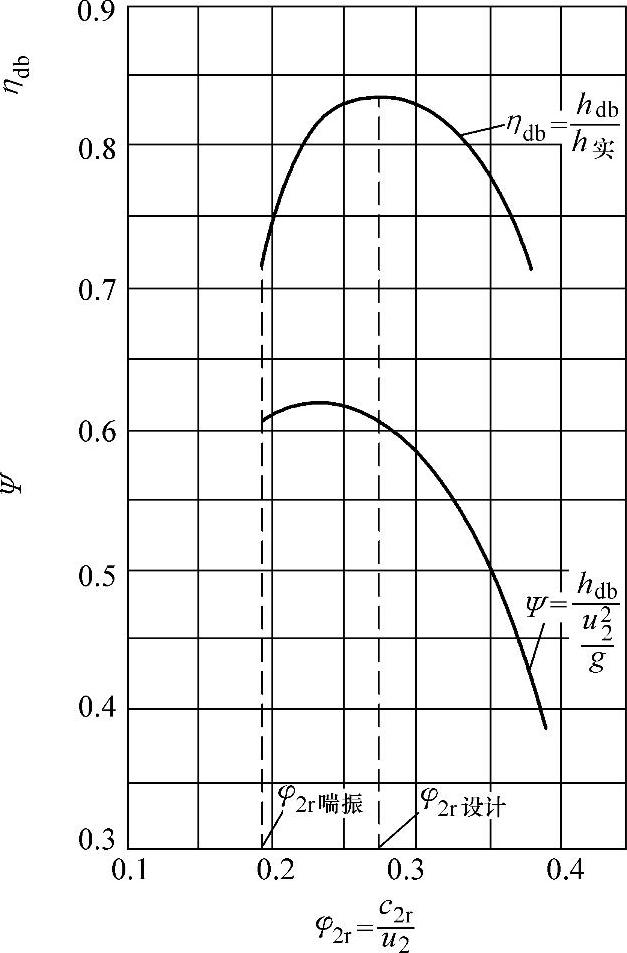
图2-15 以流量系数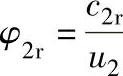、能量头系数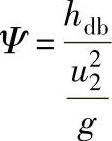和多变效率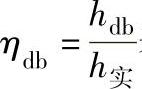表示的级性能曲线