气动特性计算：截面气流压力、比体积、体积流量和通流截面

为了便于计算离心压缩机级的压力p、比体积V和体积流量q_V在各截面上的变化，在一般设计计算中，可以把整个级中的气体状态参数的变化，看做是按照同一个多变指数m进行变化的。图2-10所示为级的气流，在同一个多变指数m下的状态参数变化。

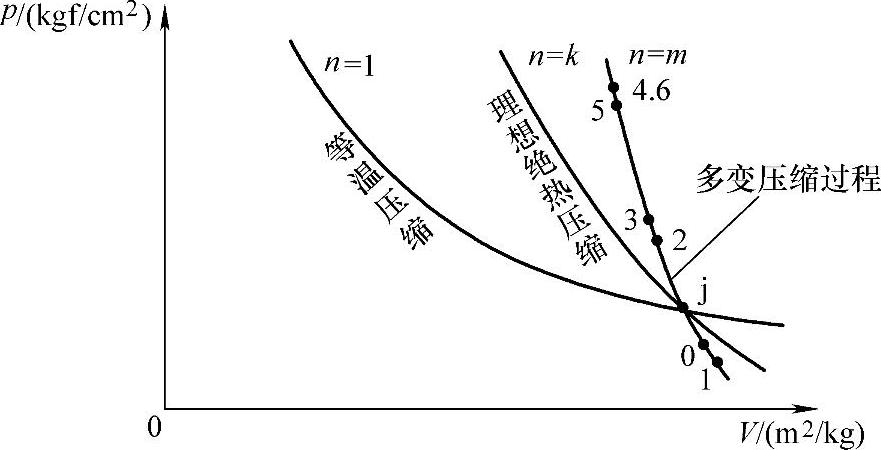
图2-10 级的多变压缩过程

多变过程pV^m=const，状况方程pV=RJ

按照热力学中的公式可以把气体在级中的气流状态参数变化表示为下列关系。

多变过程：

①压力比：

多变过程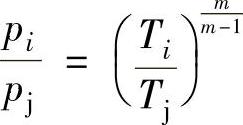

②压力：

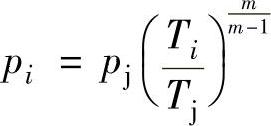
③比体积：

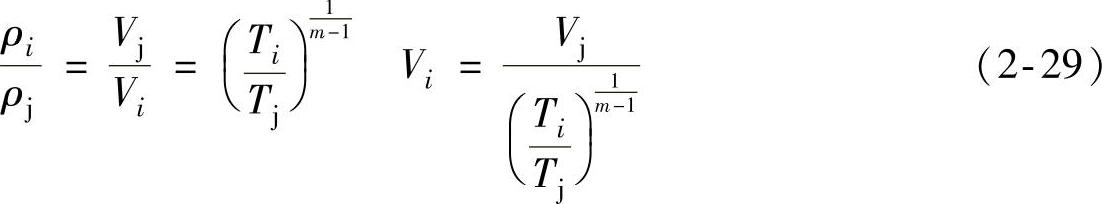
其中，p_j、Vj和Tj分别表示了级的进口气流的压力、比体积和热力学温度。而p_i、V_i和T_i则分别表示了级的任意某一截面上的气流压力、比体积和热力学温度。令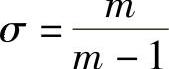，称为指数系数，可得

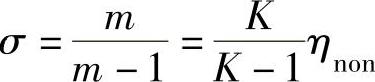
ΔT_i=T_i-T_j为任意截面上的气流温度T_i与进口气流温度T_j之差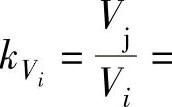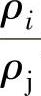；为任意截面上的气流比体积V_i与进口气流比体积V_j的比值。则在级中的气流状态参数变化关系可表示为

压力比为

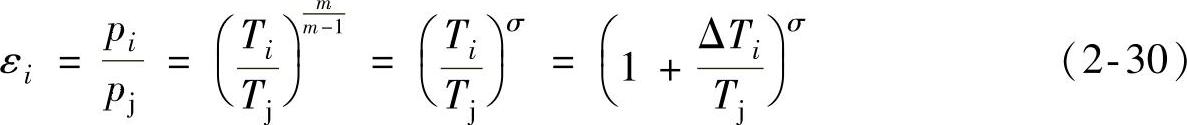
比容比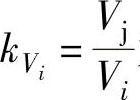为

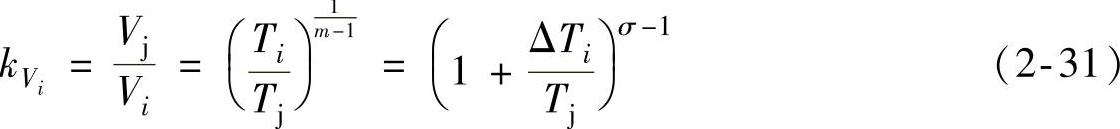
级的任意截面上的气流密度为

级的任意截面上的体积流量为

级的任意截面上的有效通流截面积为

式中 c_i——级的任意计算截面上的气流流速（m/s）。

指数系数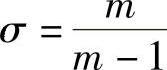的数值可按多变效率η_db的关系求取。根据热力学公式可把多变效率η_db表示为

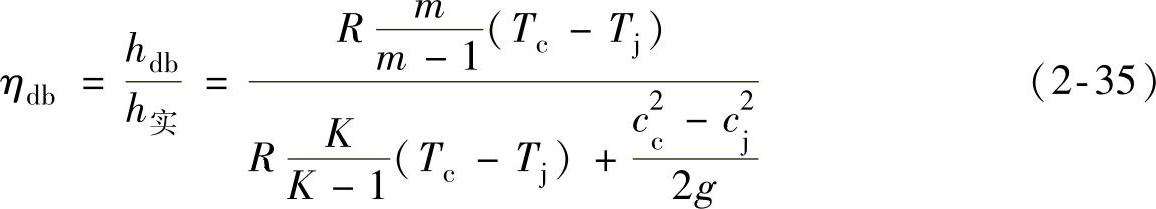
由比焓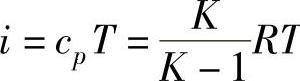，可得

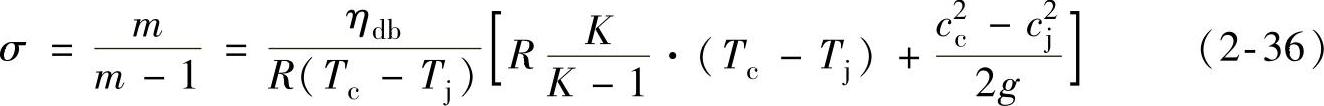
式中 η_db——级的多变效率；

T_j——级的进口热力学温度（K）；

T_c——级的出口热力学温度（K）；

c_j——级的进口气流速度（m/s）；(https://www.xing528.com)

c_c——级的出口气流速度（m/s）。

在一般压缩机级的计算中，由于进出口动能差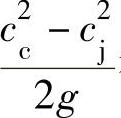很小，可以简略。这样，可以将式（2-36）简化为

忽略了级进出口动能的增加为

现在也可以把实际耗功h_实按简化关系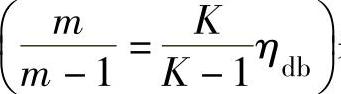表示为

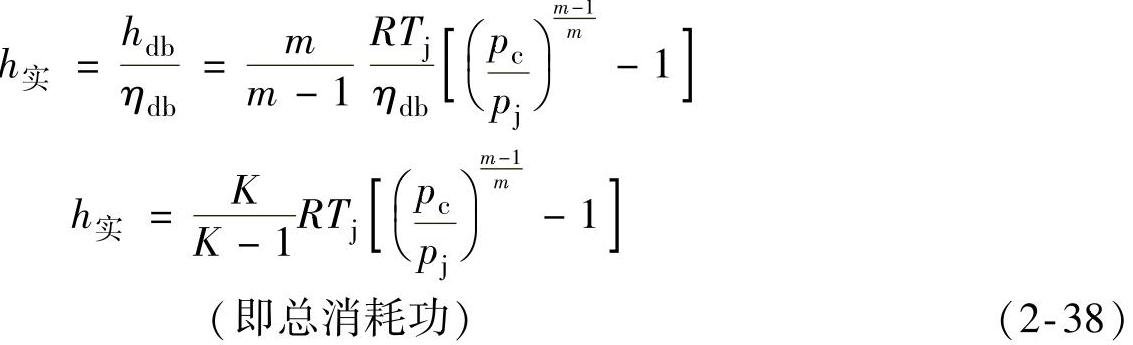
此外，还可以推导出：

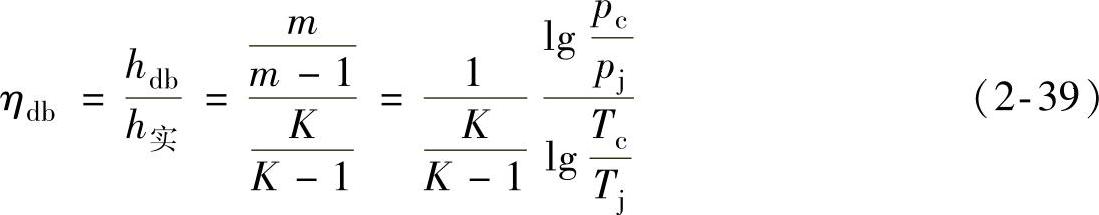
其中，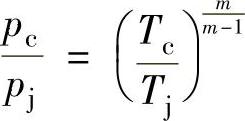

取对数后得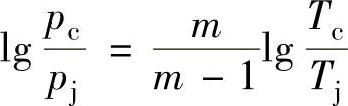

可得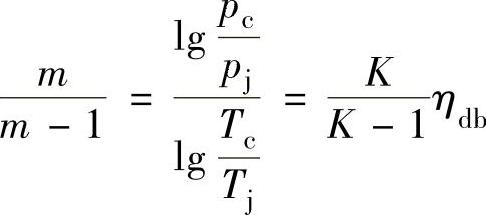

[例题2-6] 计算DA350-61型压缩机第一级各主要截面的气流压力、密度、体积流量和级的进出口通流截面。

前例的计算结果和已知条件为：级的多变效率η_db=81%；级的进口压力p_j=0.97kgf/cm²；级的质量流量q_m=6.95kg/s；级的进口温度t_j=20℃；空气的气体常数R=29.4；级的进口流速c_j=31.4m/s。

各截面情况见表2-2。

表2-2 各截面情况

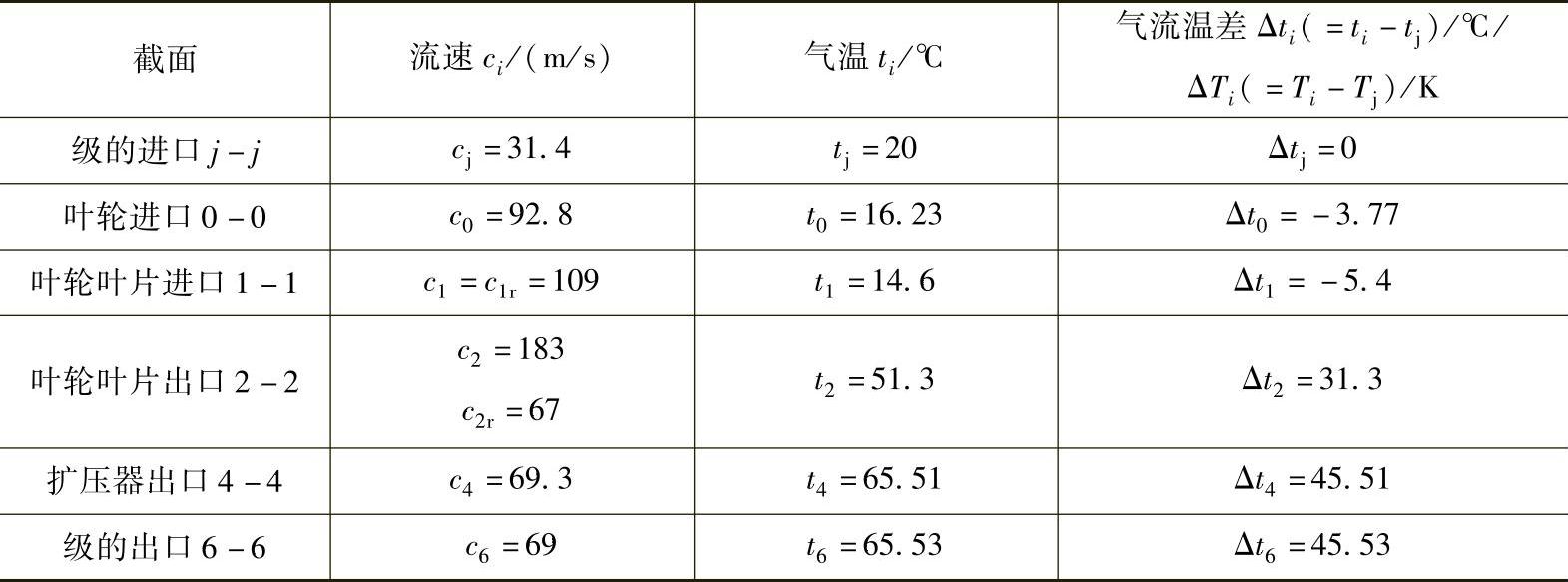
解 1）级的各主要截面上的气流压力p_i计算指数系数。

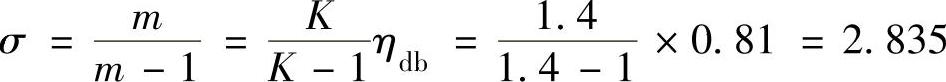
在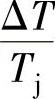值较小的情况下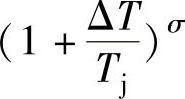，展开可简化为

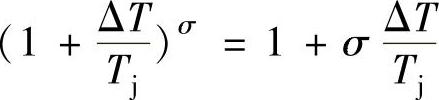
级的各主要截面上的气流压力见表2-3。

表2-3 级的各主要截面上的气流压力

2）级的各主要截面上的气流密度ρ_i的计算。

级的进口气流密度为

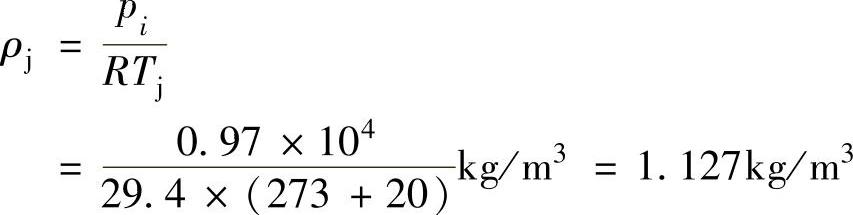
级的各主要截面的气流密度见表2-4。

表2-4 级的各主要截面的气流密度

3）级的各主要截面上的体积流量q_Vi和级的进出口通流截面积F_i的计算（表2-5）。

表2-5 级的各主要截面上的体积流量和级的进出口通流截面积