离心压缩机是通过叶轮叶片对气体进行做功的，同时也就使气体提高了能量。这种功的大小，按照动量矩定理，在一般情况下，可由叶轮出口气流圆周分速度c2u和叶轮外缘的圆周速度u2的乘积来决定，即叶轮叶片对于1kg气体所做的叶片功（能量头，也称扬程）h叶片（m）为
由图2-1所示的叶轮出口速度三角形可以看出，在圆周速度u2和气流径向分速度c2r=w2r不变的条件下，气流的圆周分速度c2u是随着气流出口角的减小（由图2-1中的β2A减小到β2）而使圆周分速度下降的（由图2-1中的c′2u下降到c2u），即叶轮叶片对气体的做功将随着叶轮气流的出口方向角β2的减小而降低。
气体在实际叶轮中流动时，气流并不是完全沿着叶片出口安装角β2A方向流出去的。气流除了具有图2-2a所示的从内径流向外径的流动外，还同时在叶片处具有图2-2b所示的轴向旋涡流动。这种轴向旋涡流动是由于气体本身具有惯性；而且气体的黏性又很小，当叶轮旋转时，气体不能跟着叶轮一起旋转而产生的。这样，相对于叶轮来说，气体在叶轮里就会出现一个与叶轮旋转方向相反的轴向旋涡。人们对于叶轮里的轴向旋涡的认识，也是从实践中得出来的，对于这种现象可以用下列实验来加以证实。
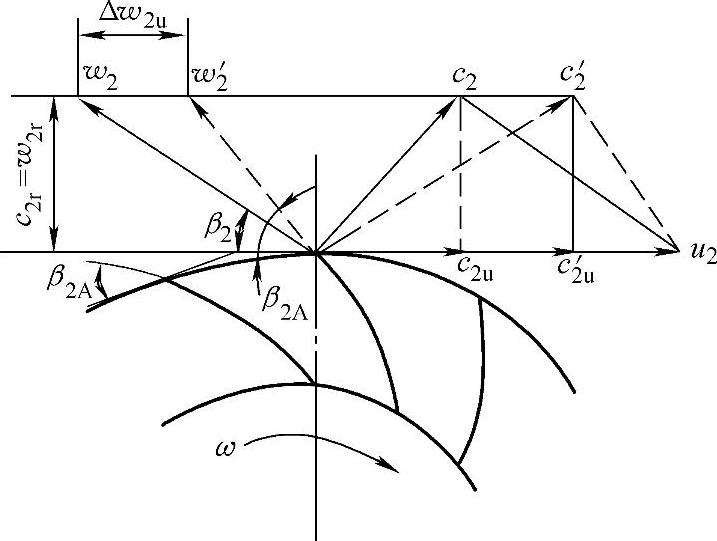
图2-1 叶轮出口速度三角形
如图2-3所示，在一盆水上浮起一片纸标。纸标的尖头N指向盆的A点，然后把水盆放在旋转圆盘上绕O点从位置①转到②、③、④，做顺时针方向旋转，这时就可以发现浮在盆上的纸标尖头N没有跟着水盆的A点一起绕圆心O点转动，而是基本上保持纸标的方向不变，这说明由于盆中液体惯性的原因，在水盆绕O点旋转时，盆中的液体只是绕O点做平移运动。同时，也可以看出，这时盆内的液体相对于水盆来说，则在做与圆盘旋转方向相反的旋转流动。这也就是叶轮在旋转时，气体在叶道中将产生与叶轮旋转方向相反的轴向旋涡流动的原因。
图2-2 叶轮叶道中的气流流动
a）径向流动 b）轴向旋涡流动
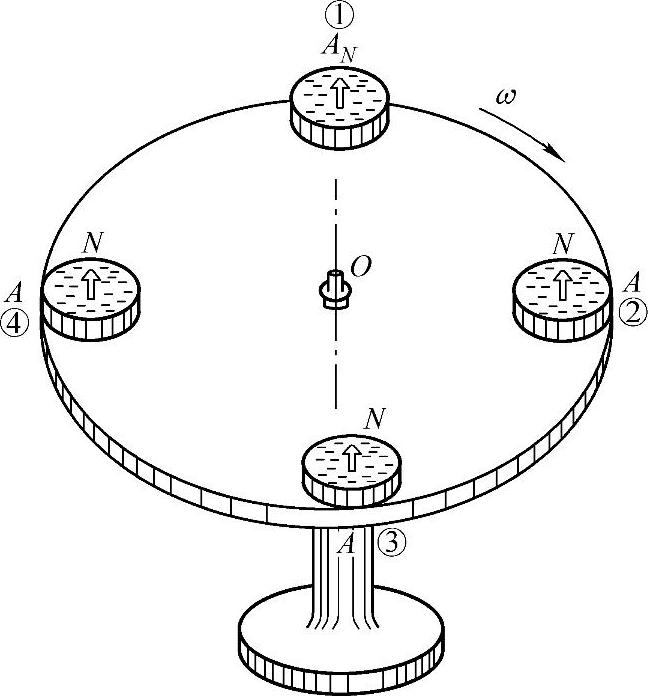
图2-3 轴向旋涡实验
如图2-2和图2-3所示，在实际工作中，由于叶轮中轴向旋涡所产生的附加速度，使叶轮出口相对速度的圆周分速度引起了Δw2u的变化，同时也使气流出口角度β2减少。这种圆周分速度的变化Δw2u，可以大致按照这样的一个旋转速度来计算，其旋涡速度等于叶轮转速，旋涡直径等于叶轮的叶道出口有效宽度。这时Δw2u可写成（由斯托陀拉推论）
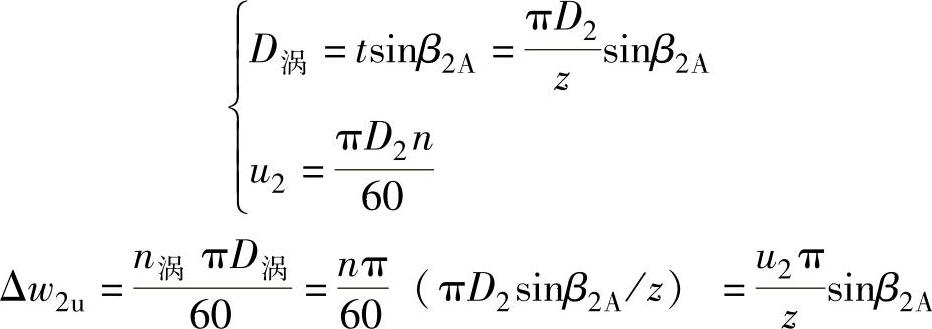
式中 Δw2u——叶轮出口相对运动速度的圆周分速度变化（m/s）；
n涡——叶轮转速（r/min），n涡=n；
n——叶轮转速（r/min）；
D2——叶轮直径（m）；
z——叶轮出口叶片数；
β2A——叶轮叶片出口安装角（°）；
u2——叶轮圆周速度（m/s）。
在Δw2u的影响下，叶轮气流出口角β2将向着减小的方向偏斜。而叶轮的气流出口圆周分速度c2u也将由于上述原因而减小Δc2u，这一项圆周分速度的减小，从叶轮速度三角形之间的相互关系可以看出，Δc2u=Δw2u，因此，由于轴向涡流存在使c2u下降，Δc2u可写成：
式中 u2——叶轮圆周速度（m/s）；
z2——叶轮出口叶片数；
β2A——叶轮叶片出口安装角（°）。
由式（2-2）可知，这种轴向旋涡的存在，将在叶片数z2较小和叶轮叶片出口安装角β2A较大的情况下，使出口气流的圆周分速度c2u显著减小。(www.xing528.com)
现在可以考虑到轴向旋涡流动的影响Δc2u，找到实际叶轮气流的出口圆周分速度c2u为
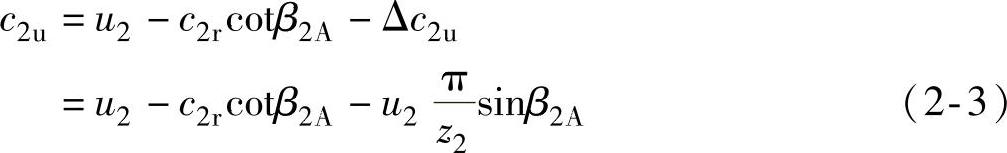
式（2-3）的等式左右都除以u2，可写成下列形式：
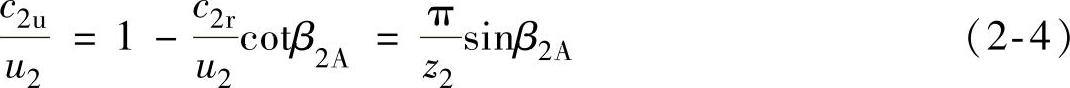
令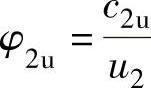 
，称为叶轮出口气流的圆周分速度系数，简称周速系数；
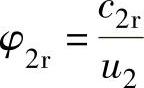，称为叶轮出口气流径向分速度系数，也称为流量系数。
可将式（2-4）写成：
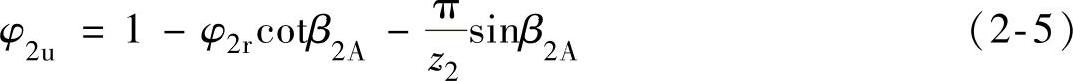
在实际叶轮中，叶片对于1kg气体所做的叶片功h叶片按动量矩定理，有限叶片数理论的能量头（kg·m/kg）为
现在，只要知道下列四项数据，即可计算出叶轮叶片在旋转时对1kg气体的做功h叶片。
下面举例应用上述所讨论的理论方法，来计算压缩机的级。
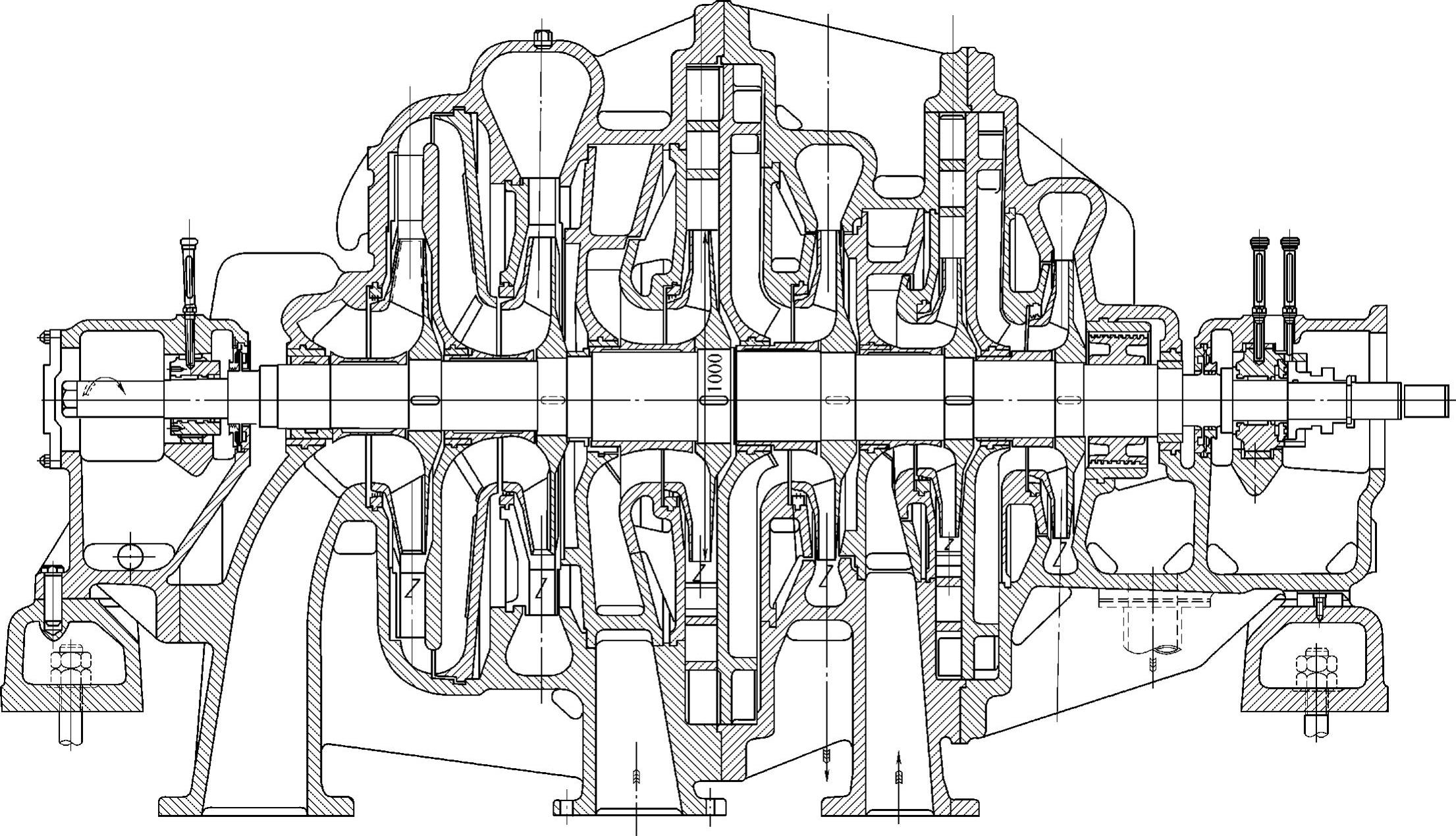
图2-4 叶轮的漏气损失
[例题2-1] DA350-61型压缩机（图2-4）第一级叶轮的外径D2=600mm，叶片出口安装角β2A=45°，出口叶片数z2=18，叶轮流量系数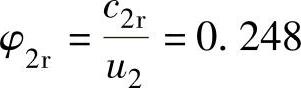
，叶轮转速n=8600r/min。
求叶轮对1kg气体所做的叶片功即能量头（扬程）h叶片。由式（2-6）
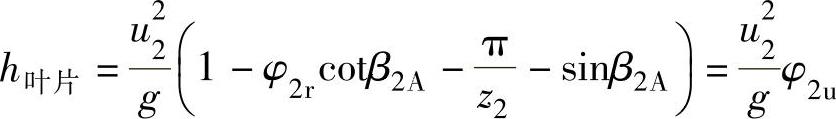
叶轮轮缘圆周速度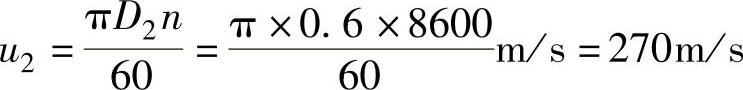
叶轮出口气流的周速系数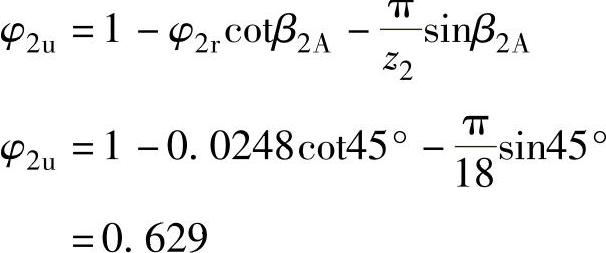
则叶片功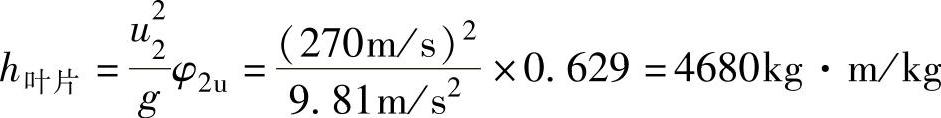
[例题2-2] DA350-61型压缩机的第一级如果不考虑级中的各种损失，已知级的进口空气压力pj=0.097kgf/cm2（1kgf/cm2=98kPa），进口空气温度tj=20℃（Tj=tj+273），气体常数R=29.4的情况，求这一级的出口压力是多少？
解 按照理想绝热过程的耗功计算公式：
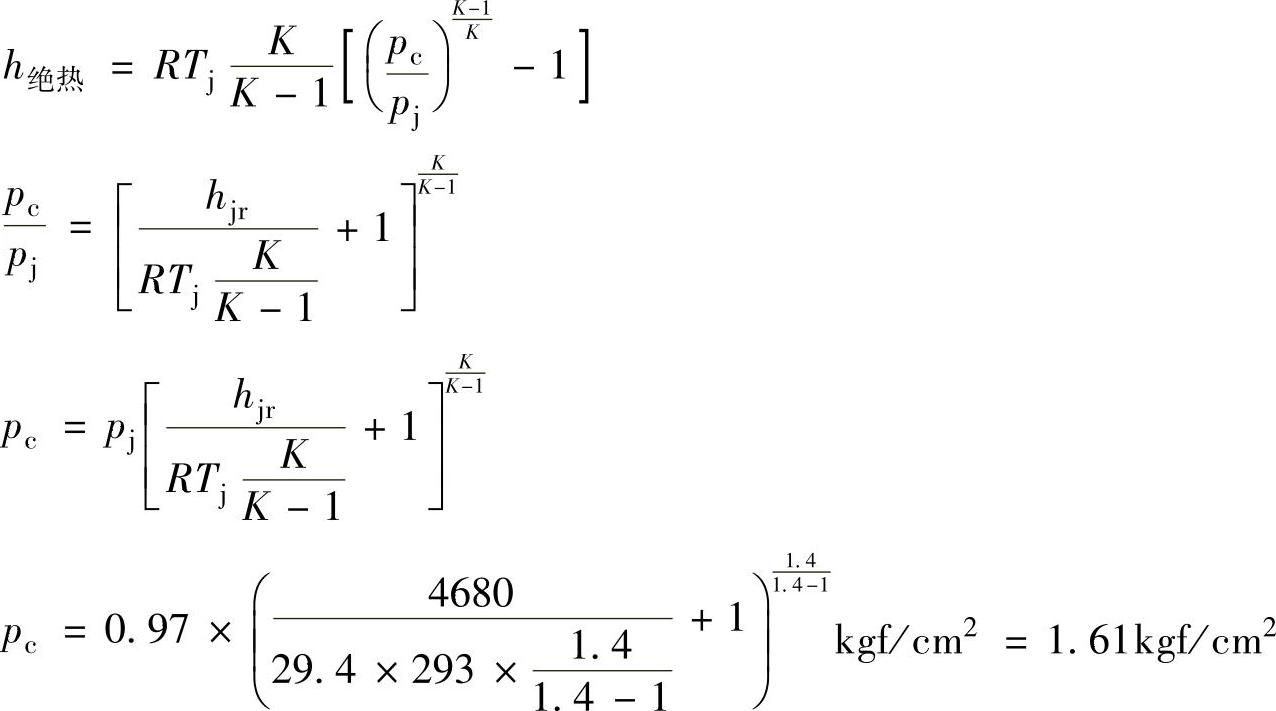
在实际工作时，由于级的各种损失存在，这一级出口的实际压力为1.46kgf/cm2。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
