无界时滞非线性正系统的μ-稳定性分析

在现实世界中，在很多情况下，系统的状态必须是非负的，例如人数、种群数等.因此需要研究正系统（positive systems）的数学模型（[26]～[27]）.其中，零解的存在性和稳定性是正系统研究中最基本的问题.

对于正的线性时不变系统（positive linear time-invariant system，记为正LTI系统）（t）=Ax（t），其为正系统的充要条件是矩阵A是Metzler矩阵（即非对角线元素为非负）.对含有时滞的正线性系统来说，文献[28]～[30]证明了时滞并不影响系统的稳定性.但是，线性系统仅占整个正系统的一小部分.最近，一类特殊的非线性系统——齐次系统的研究，取得了巨大的进步，涌现出了一些非线性正系统的研究工作.例如，文献[31]是将正线性系统推广到齐次、合作与不可约系统的先驱工作.文献[32]证明了含有常数时滞的齐次、合作系统为全局渐近稳定的（globally asymptotically stable，记为GAS），当且仅当不含时滞的系统是GAS的.文献[33]研究了度数为1的含有有界时变时滞的齐次正系统的指数稳定性；文献[34]将齐次正系统的度数从1推广到任意度数，将有界时变时滞推广到无界时滞，对于连续系统和离散系统均讨论了渐近稳定性和μ-稳定性.

本节将利用前面章节中提出的处理无界时滞系统的方法，结合坐标的非线性变换，研究含有无界时变时滞的非线性正系统的μ-稳定性.

定义8.2 对于状态空间在ℝn的动力系统，如果其初始状态在中，则其轨道始终留在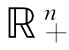，则称该系统为正系统.

定义8.3 函数f：ℝn→ℝn在ℝn\{0}上是连续可微的，如果对所有的x∈\{0}，其雅可比矩阵∂f/∂x是Metzler矩阵，则称函数f是合作的（cooperative）.

命题8.10 （[35]）设f：ℝn→ℝn是合作的.对中的任何向量x，y，其中xi=yi并且x≥y，有fi（x）≥fi（y）.

定义8.4 给定n个正实数r1，…，rn，以及λ＞0.记r=[r1，…，rn]，伸缩映射（dilation map（x）定义如下：

如果r=[1，1，…，1]，那么伸缩映射称为是标准伸缩映射（standard dilation map）.

定义8.5 如果

则f（x），x∈ℝn称为是关于伸缩映射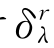（x）度为p≥0的齐次函数.

定义8.6 函数g：ℝn→ℝn在上称为是非降的，如果对任意的x，y∈，并且x≥y，有g（x）≥g（y）.

定义变换

其中ri，i=1，…，n的定义见伸缩映射.对任意的函数f，定义一个新函数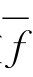（z），z=（z1，…，zn）：

函数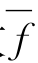（z）有如下性质.

引理8.4 如果f（x），x∈ℝn是关于伸缩映射（x）度为p≥0的齐次函数，那么（z），z∈ℝn是关于标准伸缩映射度为p≥0的齐次函数.

证明：根据（8.47），容易得到

其中=0.证毕.

引理8.5 设函数f是合作的，那么对于ℝn+中的任何向量z和w，其中zi=wi且z≥w，有

证明：首先，根据定义（8.49），若至少一个zi，wi是0，上述结论显然成立.若不然，

引理8.6 假设函数f非降并且fi（x）=Ω（xi），即存在函数d（x1，…，xi-1，xi+1，…，x__n）＞0，使得fi（x）≥d·xi，那么对中的任意两个向量z≥w，有

证明：首先，因为f是非降的，故

根据定义（8.49），有.因此，如果i≠j，则

如果i=j∈{1，…，n}，则

因此，只须验证.若其不成立，

与条件fi（x）≥dxi矛盾.

根据上述讨论，函数 是非降的.证毕.

本节要研究的连续时间表示的含有无界时滞的正的非线性系统模型为

其中xi，i=1，…，n是状态变量，φ（t）∈C（（-∞，0]，）是系统的初始状态，τ（t）为无界时滞且τ（t）＜t.

假设8.1 假设下述条件在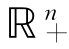上成立：

（1）f是合作的，g是非降的；

（2）f和g关于伸缩映射（x）都是度为p的齐次函数.显然f（0）=g（0）=0，因此x≡0是系统（8.52）的一个解.(www.xing528.com)

令（t）=xi（t），则

其中

根据引理8.4至引理8.6，可得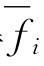和gi具有如下性质：

（1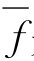）是合作的是非降的；

（2）和关于标准伸缩映射都是度为p的齐次函数.

接下来定义范数：

显然，如果‖z（t）‖{ξ，+∞}→0，那么z（t）→0及x（t）→0，t→+∞.

定理8.5 若存在正的、非降的函数μ（t）满足=+∞，并且对j=1，…，n，

则正系统（8.53）的零解是全局μ-稳定的，即zj（t）=O（μ-1（t））.

证明：由不等式（8.55），可以找到常数T，使得对任意χ≥1和所有t0≥T，

定义Lyapunov函数

其中V（t）=μ（t）·‖z（t）‖{ξ，+∞}.因此V（t）是一个非降函数，并且V（t）≤V（t）.接下来证明对所有t≥T，V（t）=V（T）.

详细证明过程略，感兴趣的读者可以参考文献[36].

若p≤1，（8.55）可被替换为

另一方面，若p＞1，许多充分条件可使不等式（8.55）成立.例如，μ·（t）/μ（t）→0，t→+∞，并且

若选取z（t）的范数如下：

对应结果可表述如下：

推论8.4 若存在正的、非降的函数μ（t）满足=+∞，并且

则正系统（8.53）的零解是全局μ-稳定的，即zj（t）=O（μ-1/r★（t）），j=1，…，n.

可通过调整参数r★使得（8.59）满足.如选取r★=1+p，从而（8.59）变为

当p=0时，不等式（8.60）为

文献[34]通过选定r★=maxiri，获得μ-稳定性的充分条件如下：

和此条件对比，条件（8.60）更加简单.更多地，若p＞rmax，因为1-＜0，所以条件（8.62）不再成立；而条件（8.60）仍成立.此优势可看作本节提出的变换的好处之一.

推论8.5 （对数稳定性）假设8.1成立且p=0，时滞τ（t）≤t-t/ln t，如果

则正系统（8.53）的零解是全局对数稳定的，即zj（t）=O（ln（t+1）-1）.

证明：选取μ（t）=ln（t+1），简单计算可得

令r★=1，不等式（8.61）等价于（8.63）.证毕.

推论8.6 （对数-对数稳定性）假设8.1成立且p=0，时滞τ（t）≤t-tα，0＜α＜1，如果不等式（8.63）成立，则正系统（8.53）的零解是全局对数-对数稳定的，即zj（t）=O（ln ln（t+3）-1）.

证明：选取μ（t）=ln ln（t+3），简单计算可得

令r★=1，不等式（8.61）等价于（8.63）.证毕.