静态网络时滞多主体系统的牵制稳定性优化

如果想让系统到达指定的一致性值的话，则需要额外的外部控制，例如，牵制控制策略.它可以通过控制少量节点来实现该目标，如下述方程所示：

其中D表示控制节点组成的集合.设｜D｜=m′，δD（i）为特征函数，即其值为1，若i∈D；反之为0.c＞0表示牵制控制的强度，s是目标值.

假设下述前提成立：

（H） G的没有外部连接的每个连通分量都至少有一个节点在D中.

命题8.1 （[1]，[2]）若假设（H）成立，则系统（8.2）在xi=s，∀i处是渐近稳定的.

在许多时滞网络化系统中，命题8.1不再成立.本节考虑下述含有传输时滞和控制时滞的模型：

其中τr表示传输时滞，τp表示牵制时滞.

当上述模型仅含有传输时滞时，文献[3]～[5]证明了，如果图含有一生成树，则能实现一致性；但是，如果一个充分大的时滞同样出现在节点的自反馈中时，在文献[6]中，证明了一致性可能会被破坏.对于时变拓扑（[7]～[9]）和异步时滞（[10]～[12]），同样现象也会出现.

然而，关于牵制时滞的研究还很少.如文献[10]，[12]都研究了对于充分小的牵制时滞的稳定性.更加精确的关于稳定性的牵制时滞条件，以及和网络拓扑、牵制节点选择等的关系，并没有成熟的研究成果.

记虚数单位为J，m×m单位矩阵为Im.图G对应的Laplace矩阵L，Lij≠0当且仅当在G中存在从vj到vi的连接.记L的特征值为{θ1，θ2，…，θm}.0总是特征值，并且其对应的特征向量是[1，…，1]⊥；而对于非零特征值θi，有Re（θi）＞0.如果G是强连通的（或者矩阵L是不可约的），则0是简单特征值.对角元素Lii称为是节点vi的加权入度.令K=diag[L11，…，Lmm]和A=K-L.

记yi=xi-s，y=[y1，…，ym]⊥，D=diag[d1，…，dm]，其中di=δD（i）.系统（8.3）可以重新写为

考虑其形式为y（t）=exp（λt）ξ的解，其中λ∈C，ξ∈Cm.因此（8.4）的特征方程可表示为

系统（8.4）的渐近稳定性等价于（8.5）的所有特征根具有负的实部.含有最大的实部的根称为主根或者主特征值.对于没有时滞的情况，命题8.1的等价表述为

推论8.1 若假设（H）成立，则系统L+cD的所有特征值均有负实部.

先给出下述引理，后面会用到.

引理8.1 对任何列向量u，v∈Cm，det（Im+uv⊥）=1+v⊥u.

首先证明，存在.如果牵制时滞τp满足τp＜，系统（8.4）是稳定的.

命题8.2 若假设（H）成立.令

并且定义

若τp＜，则系统（8.4）对所有的τr≥0都是稳定的.

证明：首先，令τp=0.证明系统（8.4）是稳定的.

如果系统（8.4）不稳定，则存在特征根λ★（（8.5）的根），使得Re（λ★）≥0.由Gershgorin圆盘定理，可知存在某个i，使得

这也意味着

因为Lii，c，di均为非负数，所以上式成立当且仅当Re（λ★）=Im（λ★）=0，即λ★=0.故exp（-τrλ★）=1.由于τp=0，因此，（8.5）等价于det（λ★Im+L+cD）=0.这与推论8.1矛盾.

因此，当τp=0时，（8.5）的特征根具有负实部.系统（8.4）是稳定的.

其次，设τp＞0.假设（8.5）有一个纯虚根λ=Jω，ω∈ℝ.根据（8.8），对于某个指标q，有

上式意味着

因此

可以证明dq≠0，即q一定是被牵制控制的节点.反之，如果dq=0，则ω=0.这也意味着0是（8.5）的一个特征根.与推论8.1矛盾.因此dq=1，即q一定是被牵制控制的节点.

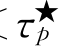不等式（8.9）可以写成F（ω，c，Lqq，τp）≤0.由的定义，对于所有的p∈D，ω∈ℝ，τp＜，F（ω，c，Lqq，τp）＞0.因此，当τp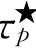＜，（8.5）没有纯虚根.根据[13]中的定理2.1，当τp＜，（8.5）的所有特征根的实部小于零.

命题8.2给出了系统（8.4）稳定的最大可允许的牵制时滞的一个估计.该估计仅需要牵制节点集合和加权入度的信息.

现在，考虑通过控制一个节点，如第q个节点，来控制整个网络.此时，D=，其中uq表示第q个标准基向量，即其第q个元素为1，而其他元素为0.如果λIm+K-A exp（-λτr）是非奇异的，利用引理8.1，特征方程（8.5）变为

命题8.3 假设（H）成立.若下述方程的所有解λ：

满足Re（λ）＜0，则系统（8.4）是稳定的.

证明：类似于命题8.2第一部分的证明方法可证：方程det[λIm+KA exp（-λτr）]=0所有解的实部小于0.因此，若（8.11）的所有解都有负实部，则（8.5）的所有根有负实部.

下面考虑两种特殊情形，以便获得关于（8.11）的解的更多信息.

第一种情形是传递不存在时滞：τr=0.简单起见，设L是可对角化的并且仅含有实根：L=Q-1 JQ，其中Q为非奇异矩阵，Θ=diag[θ1，…，θm]为实对角矩阵.此时，Q-1的列向量（Q的横向量）是矩阵L的右（左）特征向量.因此，（8.11）可写为

其中是第q个左特征向量，ξ=Q-1uq是第q个右特征向量.利用ξ和ζ的元素ξi，ζi，将（8.12）展开可得

考虑存在纯虚数解λ=Jω的最小的值τp.因此，通过分析（8.13）的实部和虚部，可以得到

其中(www.xing528.com)

因此

这也意味着a2（ω）+b2（ω）=1，且

接下来，有如下结果.

命题8.4 假设τr=0，L可对角化、不可约并且所有的特征值都是实数.设L的特征值集合{θi}排序为θq=0，并且令ζ=[ζ1，…，ζm]，=1是矩阵L对应于零特征值的左特征向量.令Z为变量为ω2的下述方程所有正解的集合：

其中a（ω）和b（ω）的定义见（8.14）.定义

则当τp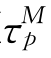＜，系统（8.4）是稳定的.

显然，（8.13）与特征值或特征向量的顺序无关.因此，命题8.4给出的关于牵制时滞的上界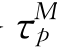不依赖于牵制控制节点的选取.

命题8.4也给出了计算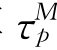的算法：

（1）找满足方程的最大解ω2：

（2）计算（8.17）.

此外，关于本节的数值模拟，感兴趣的读者可以见参考文献[14].

另一种情形是齐次性.此时矩阵L是可对角化的和可归一化的，即Lii=l，∀i，并且τr=τp.（8.11）变为

令L=QJQ-1，因此A=Q（l Im-Θ）Q-1.用上面同样的分析，（8.19）变为

此时，可以证明如下结果.

命题8.5 假设τr=τp，L是可对角化的、不可约的、可归一化的（Lii=l，∀i），其所有的特征值{θi}都是实数.记θq=0，并且令ζ=[ζ1，…，ζm]是矩阵L对应于零特征值的左特征向量，并且=1.记s表示下述方程关于变量s的解的集合：当{（W（s）/τp）-l：s∈S}的实部都是负的，其中W是Lambert W-函数（[15]），则系统（8.4）是稳定的.

利用s=τp（λ+l）exp（τp（λ+l））将（8.20）转化为（8.21），并利用命题8.3即可证明上述命题.

接下来，考虑牵制控制强度c非常小或者非常大的极端情况.将利用扰动方法（见[16，17]）去估计关于c的特征值和特征向量.

（8.5）的特征根是矩阵Σ（c，λ）=-K+A exp（-λτr）-cD exp（-λτp）的特征值.因此，当c=0时，（8.5）的特征根等于Σ（0，λ）的特征值{σi}.在假设（H）成立的条件下，存在一个简单特征值σ1=0.记Σ（c，σi）的右特征向量和左特征向量分别为，并且=1.显然，ψ1和φ1（对应于σ1=0）是矩阵L的右特征向量和左特征向量.

设λi（c）表示（8.5）的特征根表示Σ（c，λi（c））的右特征向量和左特征向量.它们都可以看成是c的函数，并且ψi，由扰动展开式（[16，17]）：

其中o（c）表示满足limc→0｜o（c）｜/c=0的项数.因此

当c充分小时，主特征值为λ1（c），因为σ1=0是c=0时的主特征值.因此，考虑i=1.此时，exp（-λ1（c）τ）=1-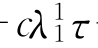+o（c）.比较两边含有c的一阶项，有

两边同时乘以，并且注意到=1，从而得到

故有如下结果.

命题8.6 设图为强连通的，并且至少一个节点被施加控制，则对于充分小的c，（8.5）的所有特征根有负实部并且主特征根由下式给出：

证明：因为图是强连通的，L含有一个简单零特征值.当c=0时，（8.5）的主特征根为σ1=λ1（0）.因为（8.5）的特征根解析依赖于c，对充分小的c，它们为λ1（c）.将（8.22）代入λ1（c）并且注意到（-K+A）φ1=0，即可得到（8.23）.

为了理解（8.23）的含义，考虑一个特殊情形，即对称矩阵并且邻接矩阵的值为0或者1.因此，φ1=[1，…，1]⊥，ψ1=[1，…，1]⊥/m，有=，即图的平均度数（mean degree）.不仅如此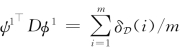，，即控制节点所占的比例（pinning fraction）.故，（8.23）得到如下估计：

因为主特征值的实部衡量系统指数收敛的速度，因此命题8.6意味着，对于充分小的c，如果控制节点的数目增加，或者传输时滞减小，或者平均度降低，都可以改善收敛速度.

接下来，考虑c比较大的情况.令ε=1/c及μ=λ/c，（8.5）可以写为

根据之前的结果，当ε充分小时，等价于c充分大，对（8.4）来说牵制时滞的最大允许值会接近0.自然地就可以假设τp以下述方式依赖于c：当c变大时，τpc是有界的.因此，假设当c→+∞时，τpc：=τpc有界.

当ε=0时，（8.25）接近于

其中τp∞是在之间的任何值.以元素的形式表示为：如果i∈D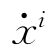，=-xi（t-τp∞）；反之为0.当ε=0时，（8.25）的特征方程可写为

其中m′=｜D｜.众所周知，函数μ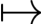μ+exp（-μτp∞）的所有根的实部Re（μ）＜0当且仅当τp∞＜π/2.因此，加上条件：τpc＜π/2.

因此，（8.26）的解的最大实部是0，对应的解为μ=0，对应的特征空间有m-m′维，具有形式

不失一般性，假设D={1，…，m′}.零特征值μi对应的右和左特征向量ξi，ζi∈ES，使得=1，并且=1，i≠j，i，j=m′+1，…，m.在μi附近关于ε进行扰动，即μi（ε）是（8.25）扰动后的解，是对应的右和左特征向量.由扰动展开式，当ε→0时，

根据（8.25），

命题8.7 设图为强连通的，并且至少一个节点被施加控制.固定τr≥0，设τpc＜π/2，c→+∞.那么（8.25）的主根有下述形式：

其中是下述时滞微分方程的主特征值：

更多地，对所有充分大的c，Re（λ（c））＜0.

证明：条件τpc＜π/2意味着，当ε=0时，特征方程（8.25）的主根是0，特征子空间为ES.因此，对充分小的ε，方程（8.25）的主根和对应的特征向量有形式（8.27），其中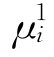满足（8.29）的第一个方程，即是（8.31）的特征值.因为λ（ε）=μ/ε，可得（8.30）.更多地，因为-K2+A22是对角占优的，在假设（H）下有＜0，所以对充分大的c，系统（8.3）的所有特征值都有负实部.