时滞非线性耦合系统的同步方法

在现实世界中，很多情况下都无法直接观测到状态变量xi（t）的值.相反地，观测到的数据是状态的一个非线性函数值g（xi（t））.本节将利用该观测数据来实现同步耦合系统.有些文章（[12]～[14]）研究过离散系统非线性耦合含有或不含有时滞的同步.但对于非线性耦合下的连续系统，仅有少量文章（[15]）研究了其全局同步.

考虑如下含有时滞的非线性耦合复杂网络：

即矩阵M含有N（N-1）/2行.而对于每一行，其至多含有2个非零元素.矩阵B的不可约性质保证了对任意的指标对i和j，存在指标i1=1，i2，…，il=j和p1，…，pl-1，使得≠0，1≤q＜l.

容易知道，U∈A3，并且UA=-A.根据上述引理，U可表示为U=-M⊥M.易知

引理7.3 x（t）∈S当且仅当‖（M⊗In）x（t）‖=0，其中S是同步子空间.

首先给出不依赖于时滞的全局指数同步判定定理.

定理7.7 假设f∈QUAD（P，D，α），gj∈UNI，并且存在对称矩阵U1∈A3，使得下式成立：

其中U的定义见（7.30），且

则耦合系统（7.29）是全局指数同步的.(www.xing528.com)

证明：假设U1=-.定义Lyapunov函数

其中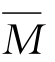=M⊗In.对其求导，并进行一些代数运算，即可得证.详细证明略.感兴趣的读者可以参考文献[16].

需要特别说明的是，根据条件（7.31），可以看出：耦合系统的全局同步稳定性如果是不依赖于时滞的，则所有的πj，j=1，…，n应该是负的.也就是说，未耦合系统应该是稳定的.

接下来给出依赖于时滞的全局指数同步判定定理.

定理7.8 如果下述条件满足：

其中β1=‖A‖，β2=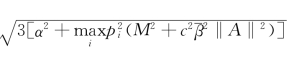，则耦合系统（7.29）是全局指数同步的.

证明：定义Lyapunov函数如下：

其中参数k需要满足某些条件.对其求导，并进行一些代数运算，即可得证.详细证明略.