线性矩阵不等式求解方法探讨

Lu和Chen（2003）在文献[4]中，讨论了如下时滞神经网络：

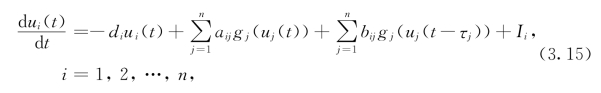
其中，bij表示第j个神经元在时刻t-τj对神经元i的连接系数，τj≥0是神经元j的信号输出时滞.

令u=[u1，u2，…，un]⊥，D=diag[d1，d2，…，dn]，g（u）=[g1（u1），g2（u2），…，gn（un）]⊥，I=[I1，I2，…，In]⊥，τ=[τ1，τ2，…，τn]⊥，A=[aij]，则系统（3.15）可写为如下之矩阵形式：

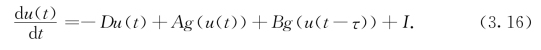
引理3.2 （[4]引理2）假设g∈H1（G1，…，Gn）（Gi＞0，∀i=1，…，n），且存在正定对角矩阵P和Q，使得

那么系统（3.16）有唯一的平衡点.

证明：由条件（3.17）可知：

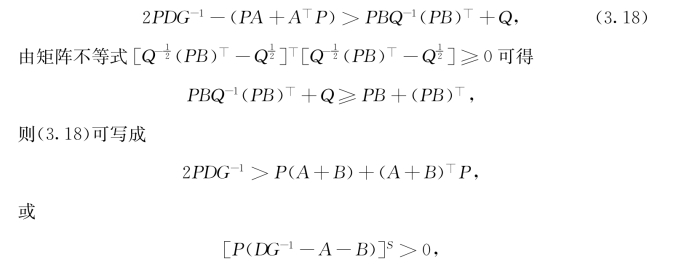
即DG-1-（A+B）∈LDS（见[4]引理1）.可知，H（u）=-Du+Ag（u）+Bg（u）+I是一个从ℝn到ℝn的同胚.所以系统（3.16）有唯一的平衡点.□

定理3.5 （[4]定理1）假设g∈H1（G1，…，Gn）（Gi＞0，∀i=1，…，n），且存在正定对角矩阵P和Q，使得

成立，则系统（3.16）有唯一的平衡点，而且是全局指数稳定的.

证明：由引理3.2可知，系统（3.16）有唯一平衡点u*.通过平移变换x（t）=u（t）-u*，方程（3.16）可写成

其中x（·）=[x1（·），…，xn（·）]⊥，φ（·）=[φ1（x1（·）），…，φn（xn（·））]⊥，，i=1，2，…，n.显然，u*的全局指数稳定性等价于系统（3.20）在原点的全局稳定性.

定义Lyapunov泛函：

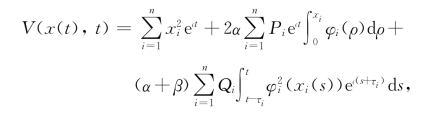
其中正常数∈＞0充分小，α和β待定.对V沿着（3.20）的解轨道求导可得

现在，我们选取参数ε，α，β，使得.首先，固定β满足

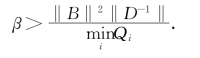
然后，取充分小的ε＞0和充分大的α＞0，使得

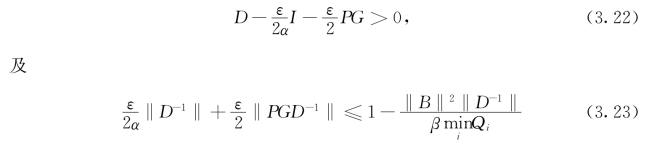
成立.由（3.19）可得

对于充分大的α和充分小的ε成立.

结合（3.23）和不等式‖（I-F）-1‖≤，当‖F‖≤1（参见[6]），我们得到

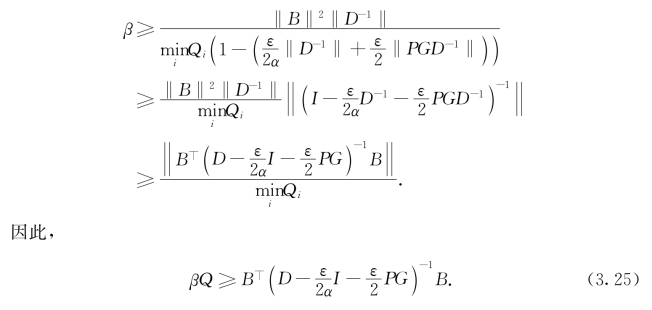
至此，对于已选出参数，不等式（3.24）和（3.25）成立.

我们再证明（x（t），t）≤0.注意到D-PG是正定矩阵，由式

（3.22），我们有

类似可得

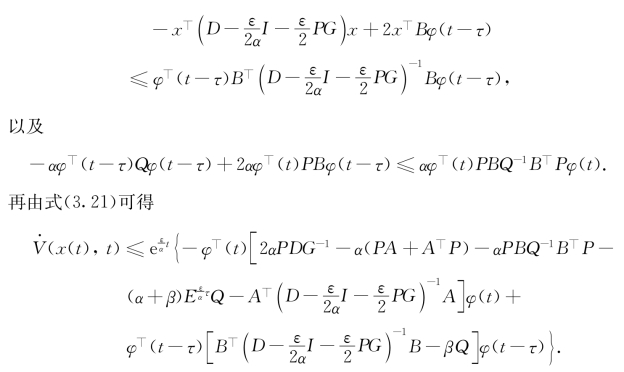
综合（3.24）和（3.25）可得

所以，V（x（t），t）≤V（x（0），0）.因此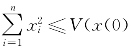，，0）e-∈t.这就是说，对系统（3.20），x=0是全局指数稳定的.定理3.4得证.(www.xing528.com)

上述定理条件的验证是基于线性矩阵不等式（linear matrix inequality，LMI.可参看[7]）.

利用Schur互补定理（引理2.20），我们有

定理3.6 （[4]定理2）设P=diag[P1，…，Pn]，Q=diag[Q1，…，Qn]，Pi＞0，Qi＞0，i=1，2，…，n，则

等价于下述矩阵线性不等式

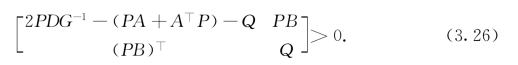
因此，如果（3.26）成立，则系统（3.16）平衡点唯一存在，且是全局指数稳定的.

注3.5 当所有τj=τ时，即考虑下述系统：

定理（3.5）中的对角阵Q可以改成任意正定对称阵Q.即成立着

定理3.7 假设g∈H1（G1，…，Gn）（Gi＞0，∀i=1，…，n），并且存在正定对角阵P和正定对称阵Q，使得

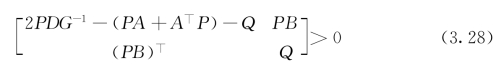
成立，则系统（3.27）有唯一的平衡点，而且是全局指数稳定的.

类似地，对于Cohen-Grossberg神经网络

Chen和Rong（2003）在文献[21]证明了

定理3.8 假设α2≤ai（·）≤α1，，g∈H1（G1，…，Gn）（Gi＞0，∀i=1，…，n），并且存在正定对角阵P和Q，使得

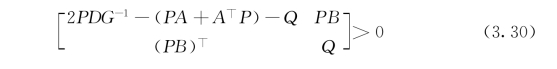
成立，则系统（3.29）有唯一的平衡点，而且是全局稳定的.

注3.6 当τj=τ时，即

应用[21]引入的方法，现在证明

定理3.9 假设α2≤ai（·）≤α1，bi（x）-bi（y）≥di（x-y），g∈H1（G1，…，Gn）（Gi＞0，∀i=1，…，n），并且存在正定对角阵P和正定对称阵Q，使得

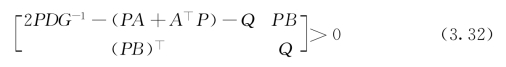
成立，则系统（3.31）有唯一的平衡点，而且是全局稳定的.

证明：由[5]中的定理1，系统（3.31）存在唯一平衡点u*.通过平移变换x（t）=u（t）-u*，方程（3.16）可写成

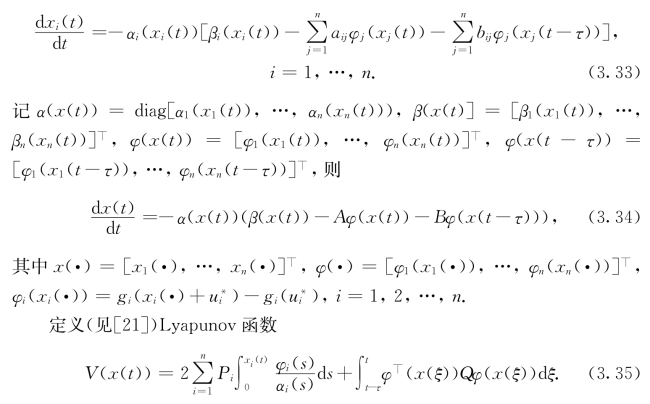
求导得

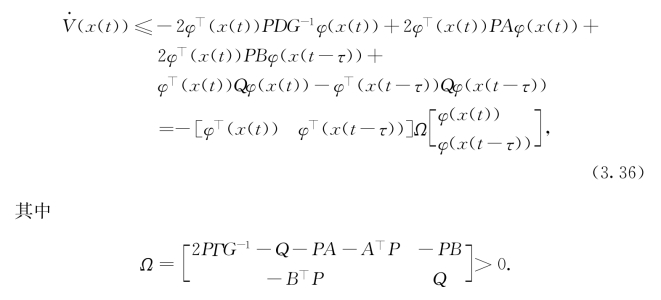
由LaSalle不变原理可证得定理（细节从略）.

由定理3.6，系统的全局稳定性可化为验证矩阵线性不等式（3.26）.我们可利用Matlab中的线性矩阵与控制工具箱（LMI and Control Toolbox）来寻找P和Q，使得（3.26）满足.更多关于LMI的细节参看[7].下面，我们将举一个例子来描述如何验证定理中的结果.

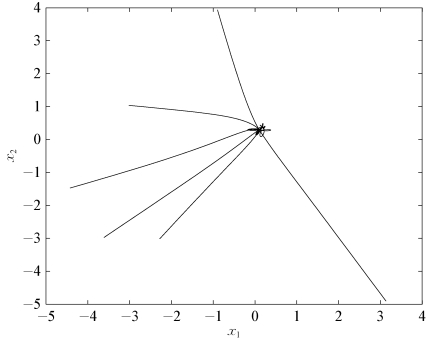
图3.1　系统（3.37）的全局稳定性

例3.1 考虑如下两维系统：

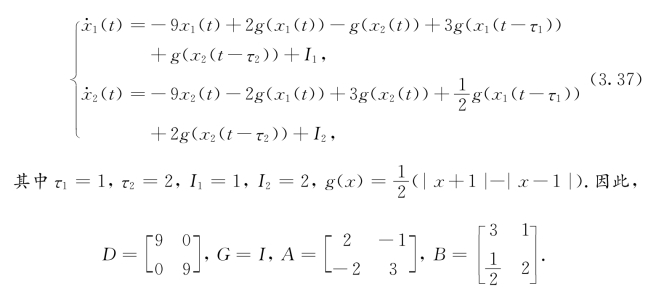
我们利用Matlab中的线性矩阵与控制工具箱可求得P=diag[0.091 2，0.121 5]，Q=diag[0.091 2，0.121 5].此时，

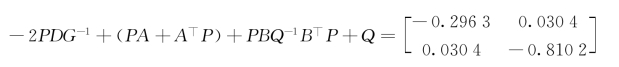
的特征根为-0.812 0，-0.294 5.故定理3.5的条件满足，系统（3.37）全局稳定.

如图3.1所示，初值分别为[sin（s），cos（s）]，[log（s+3），s2]，[s3，arctan（s）-4]，[27，-45]，[tan（s）-3，-（s+10）1/3].这里s∈[-2，0].