时滞泛函微分方程与时滞差分方程

由于本书中的大部分章节都将用微分方程或者差分方程来描述我们所研究的神经网络或者复杂网络，在此我们简要介绍一下这两类方程的相关知识.

首先简单介绍一下时滞泛函微分方程（retarded functional differential equations，RFDE）的概念及相关理论.详细的内容可以参看[1].我们后面将要研究的时滞神经网络

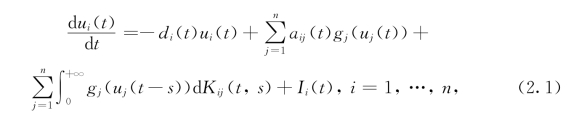
就属于一类重要的时滞泛函微分方程，即如下的Volterra泛函微分方程（VFDE）：

令r≥0为一个给定的实数，C（[a，b]，ℝn）为将区间[a，b]映射到ℝn的连续向量值函数在一致收敛拓扑下构成的Banach空间.如果[a，b]=[-r，0]，则简记C（[-r，0]，ℝn）为C.对于φ∈C，定义范数‖φ‖=sup-r≤θ≤0｜φ（θ）｜.如果σ∈ℝ，A≥0，x∈C（[σ-r，σ+A]，ℝn），那么对于任意的t∈[σ，σ+A]，定义xt∈C为xt（θ）=x（t+θ），-r≤θ≤0.给定区域D⊆ℝ×C以及D上的映射f：D 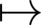ℝn，令“·”表示关于t的导数，那么称

为一个时滞泛函微分方程.如果存在σ∈ℝ，A＞0，以及函数x∈C（[σ-r，σ+A]，ℝn），使得（t，xt）∈D，并且xt在t∈[σ，σ+A）上满足方程（2.3），那么称x是方程（2.3）的一个解.对于给定的σ∈ℝ，φ∈C，如果xt（σ，φ，f）是方程（2.3）的解，且满足xσ（σ，φ，f）=φ，那么称xt（σ，φ，f）是方程（2.3）在σ处初值为φ的解，或者简称为穿过（σ，φ）的解.

泛函微分方程有着与常微分方程类似的定性理论.下面对其解的存在唯一性及延拓定理进行简单的介绍.

引理2.1 假设X是ℝ×C中的一个开集，f：X 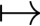ℝn是连续的，并且f（t，φ）在X的每一个紧子集上关于φ都是Lipschitz的.如果（σ，φ）∈X，那么方程（2.3）有唯一解穿过（σ，φ），并且这个解的存在区间要么是无穷，要么可以延拓到X的边界.

下面给出泛函微分方程稳定性的相关定义.

定义2.1 假设xt=0是方程（2.3）的一个解.如果对于任意的σ∈ℝ，ε＞0，都存在δ=δ（σ，ε）＞0，使得当φ∈B（0，δ）时，xt（σ，φ，f）∈B（0，ε）对所有t≥σ都成立，则称方程（2.3）的零解是稳定的.如果方程（2.3）的零解是稳定的，且存在b0=b0（σ）＞0，使得当φ∈B（0，b0）时，limt→+∞xt（σ，φ，f）=0，那么称方程（2.3）的零解是渐近稳定的.如果b0=+∞，那么就称方程（2.3）的零解是全局渐近稳定的.进一步，如果存在常数K＞0，α＞0，使得‖xt（σ，φ，f）‖≤K‖φ‖e-α（t-σ），那么称方程（2.3）的零解是全局指数稳定的.

由方程（2.3）的零解的稳定性可以更一般地定义其任意解的稳定性.对于方程（2.3）的任意解yt，如果方程

的零解是稳定的，那么称yt是稳定的.在此基础上，其他的稳定性概念也可类似定义.

此外，对于自治泛函微分方程，也存在Lasalle不变原理.下面我们给以简单介绍，详细的可以参看文献[2].

令f：X⊆C 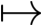ℝn为连续映射，考虑如下的自治泛函微分方程：

(https://www.xing528.com)

对给定的φ∈X，令xt（φ）为（2.4）的从（0，φ）出发的唯一解，令I（φ）=[0，ω（φ））为xt（φ）的最大存在区间，定义χ={（t，φ）：t∈I（φ），φ∈X}.定义映射π：χ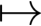X为π（t，φ）=xt（φ），则称π为由（2.4）的解定义的X上的流.

定义2.2 对给定的φ，ψ∈C，如果存在一个序列{tn}⊆I（φ），且当n→+∞时tn→ω（φ），π（tn，φ）→ψ，则称ψ为π（t，φ）的一个正向极限点，π（t，φ）的所有正向极限点的集合称为π（t，φ）的正向极限集，记为Ω（φ）.

定义2.3 对给定的φ∈X，令xt（φ）为（2.6）的从φ出发的唯一解，定义γ+（φ）=π（I（φ），φ）={xt（φ）：t∈I（φ）}为从φ出发的正向轨道.如果⊆X并且是紧的，那么就称xt（φ）是列紧（precompact）的，即γ+（φ）相对于X是列紧的，也等价于γ+（φ）相对于C是列紧的，且Ω（φ）⊆X.显然，如果xt（φ）是列紧的，那么I（φ）=[0，+∞）.

对于给定的函数V：X 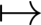ℝ，定义它相对于（2.4）的导数为

定义2.4 令G为X的一个子集，如果函数V满足：

（1）V在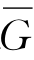或X上连续；

（2）对于所有的那么称V是G上的Lyapunov函数.

如果V是G上的一个Lyapunov函数，令E=，M为E中的最大不变集，那么我们有如下的Lasalle不变原理.

定理2.1 令V为方程（2.4）在G上的一个Lyapunov函数.如果x（t，φ）是方程（2.4）的一个列紧解，并且对所有t≥0都有xt∈G，那么存在一个常数c，使得当t→+∞时，xt→M∩V-1（c）.

差分方程是一种递推关系，也可以看作微分方程的离散化，是微分方程进行数值计算的一种途径.但是与微分方程相比，差分方程具有更丰富的动力学性态，在数学的理论研究方面具有更大的挑战性.令t∈ℕ为离散时间，则一个差分方程实际就是一个递推序列：

其中，x（t）∈ℝn，τ是一个正整数，f：对于固定的t是一个连续映射.方程（2.6）称为一个τ-阶差分方程.它的解是一个当t≥τ时满足方程（2.6）的序列.由于方程（2.6）是一个递推序列，因此如果给定初始条件，就可以依次计算出x（τ），x（τ+1），….

下面对于差分方程的平衡解和稳定性进行简单介绍，更详细的内容可以参看文献[3]及其中的参考文献.

定义2.5 若存在x*，使得x*=f（t，x*，…，x*），则称x*是（2.6）的一个平衡点.设x（t）是差分方程（2.6）的解，若有正整数T，使得x（t+T）=x（t）对所有的t∈ℕ都成立，则称x（t）是差分方程（2.6）的周期解，T称为周期.

定义2.6 设x*是差分方程（2.6）的平衡解，x（t，）是方程（2.6）的以为初值的解，如果对任意给定的正数ε，都存在δ＞0，使得当maxt=0，…，τ-1｜φt-x*｜＜δ时，｜x（t，）｜＜ε对所有t∈ℕ都成立，则称差分方程的平衡解x*是稳定的，否则称为不稳定的.如果有正数η，使得只要就有limt→+∞x（t，）=x*，则称x*是吸引的；如果η=+∞，则称x*是全局吸引的.如果x*既是稳定的，也是（全局）吸引的，就称x*是（全局）渐近稳定的.

对于自治的时滞差分方程，也存在Lasalle不变原理，有兴趣的读者可以参看相关文献或者模仿自治泛函差分方程的例子自己给出，在此从略.