时滞耦合复杂网络的动力学模型

复杂网络是具有海量节点数和复杂连接拓扑结构的网络模型（[24]）.不仅如此，复杂性还包括节点复杂的动力学行为.它不仅包含线性和有序的模型，还包括非线性（nonlinear）和时空混沌（spatiotemporal chaos）.复杂网络已成为近年来研究的主要对象.

总而言之，复杂网络动力系统是具有复杂动力学行为和复杂拓扑结构的网络.在现实世界中，有很多系统都可以看作复杂网络动力系统.熟知，Laplace矩阵和邻接矩阵可用来描述一个图.设节点编号为（1，2，…，n），共n个节点.对于邻接矩阵G=（gij），i≠j，i，j=1，…，n，描述了节点i和节点j的连接关系：gij=1表示i和j相互连接；gij=0表示i和j互不连接.在邻接矩阵中对角元gii都取零，而在Laplace矩阵L=（lij）中，相互连接的i和j对应lij=-1；反之，lij=0.对角元lii取为节点i的连接度：与节点i相连接的节点数目，即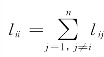.可见L=W-G，这里W=diag{l11，l22，…，lnn}.

20世纪60年代，Erdös和Rényi提出了随机图的模型来描述复杂网络的拓扑（[25]），由此发展出的随机图理论研究了在图的节点数趋于无限大时，一些概率空间中的统计量的分布.这是图理论的一个重大突破.近年来，随着高性能计算机和大规模数据库的飞速发展，使用计算模拟的方法处理大尺度（large-scale）网络成为可能.这样，一些新的介于固定网络和完全随机网络的网络模型被提出来研究.在文献[26]中，作者提出了小世界网络模型（small-world）.小世界网络是介于固定网络和完全随机网络的一类过渡网络；在文献[27]中，一种名为无尺度网络（scale-free）的模型被提出来.

由此可见，对系统的动力学研究不应当仅限于单个个体或者简单网络上，而应该着眼于复杂网络：复杂网络的拓扑性质对动力学形态的影响、复杂网络上非线性动力系统的动力学行为都应是研究对象.

本书中，我们将把系统的动力学行为分析放在复杂网络这个平台上进行.单个个体的动力学特征和拓扑特性对网络动力学形态的影响将成为研究的重点.

一个系统的各个子系统可能并不相同，但子系统并非孤立于其他子系统之外.事实上，它们之间有相互影响、相互连接（interaction）和相互耦合.这种连接可能很弱，但正是子系统间的连接，使得各子系统可根据其他系统的状态来调整自己的状态，从而实现整体协调性（coordination）.所谓协调性，就是研究网络节点间的相互作用如何导致的整体化行为.这个概念在不同学科背景中，有着不同的表述.整体的行为和状态的协调性行为是局部个体间相互作用产生的结果.在鱼群中，每条鱼会依据周围鱼的运动来调整自己的运动状态，形成整个鱼群向中心聚集，且朝同一方向运动的形态.在传感器网络（sensor network）中，每个传感器追踪其邻接传感器的平均状态，从而使网络的校正状态调整到一致，使之协调工作.耦合震荡子（coupled oscillators）依据与之耦合的其他震荡子的相位来调整自己的角速度，从而达到同步.显然，网络拓扑结构对协调性行为有重要影响，这是本书所关注的核心内容之一.而且在实际中，网络结构可以随时间动态演化.例如，运动鱼群中的每条鱼的位置和运动方式总是不断变化的，从而它们间的相互影响也是变化的.移动中的传感器（mobile sensor），可能离开某一传感器的影响范围，也可能进入另一传感器的有效区域，从而导致它们之间连接消失或出现.另一方面，个体的动力学行为也会影响网络的整体协调性行为特征.不同的初始状态和点动力学行为，不仅影响网络能否达到协调性，也会影响网络协调的状态.

本书对复杂网络的协调性行为的研究，包含三方面的内容.

（1）复杂网络同步.复杂网络同步行为的研究近年来吸引了众多数学、物理和系统科学研究者的兴趣.“同步”（synchronization）一词源于希腊语词根（chronos，意为时间）和（syn，意为相同）的组成，意为“共享相同的时间”.当今，同步意指自然科学、社会科学和工程技术中广泛存在的一大类现象：表现为不同的进程对于时间的一致性.自17世纪惠更斯发现两个弱连接的钟摆的相位同步（参见[28]）以来，人们观察到大量的同步现象并作了研究，如萤火虫闪烁的一致性、管弦乐队小提琴的协同、心脏频率和呼吸、运动频率的一致性，以及激光发生器的同步性等.

同步现象的研究，可以帮助人们更清楚和深刻地认识自然和世界.例如，Mirollo和Strogatz建立了描述萤火虫同步闪烁机制的模型（参见[29]，耦合有时滞时，见[30]）；Fries等人和Stein等人发现人类和灵长目动物注意力的选择与神经元的激发率（firing rate）无甚关系，却与神经元的同步率（synchronous rate）紧密相关（参见[31，32]）.而且，由同步现象发展起来的技术已在实际中有着广泛的应用.[33]等大量文章致力于利用主从系统（master-slave）实现混沌安全传输；Kunbert等提出了利用同步生成自动波（autowaves）来解决图像处理中的问题（参见[34，35，36]）.

一个系统的各个子系统的动力学形态可能并不相同，但在各个子系统之间，存在着连接、耦合，从而相互间会产生影响.通过这种连接，各子系统可根据其他系统的状态来调整自己的状态，从而实现同步.这种相互的连接正是产生同步的最根本的原因（[37]）.相互间的这种连接对同步的影响的研究正是本书的重点之一.

数学上，可以定义完全同步（complete synchronization）、相位同步（phase synchronization）、时滞同步（lag synchronization）、分群同步（cluster synchronization）、部分同步（partial synchronization）和广义同步（generalized synchronization）等（参见[38]）.本书着重研究的是完全同步，其定义如下.

定义1.1 记系统中节点vi的状态变量为xi（t），i=1，…，m，若xi（t）=xj（t）或者

对所有i，j=1，…，m成立，则称网络（或系统）达到同步.在本书中，如无特别说明，简称为同步.

（2）多主体网络一致性（consensus）.一致性是同步现象之外复杂网络上的又一种特殊而重要的协调性现象.一致性问题与同步问题紧密相关，甚至可以说，一致性问题是一类特殊的同步问题.也正由于这种特殊性，使其有独立研究的价值.在多个体系统中，一群协作的个体为了实现共同目标需要在某个感兴趣的量上达成一致，这就是通常所说的一致性或者趋同性问题.本书统一采用“一致性”这一名称.当今，一致性问题大量出现在多个体系统的应用领域中.例如，分布式计算（[39，40，41]），鸟类的聚集（[42，43]），无人驾驶车辆的协同控制（[44]），分布式滤波器（[45]），分布式感知网络（[46，47]），等等.而且，由于多个体系统的广泛应用，一致性问题也得到越来越多的关注.

网络实现一致性的数学定义如下.

定义1.2 称多个个体（t）∈ℝ实现了一致性，如果存在与节点vi无关的α∈ℝ（依赖于初始状态），对所有i=1，…，m，有

或弱一致性：对所有i，j=1，…，m，(www.xing528.com)

可见，弱一致性本质上就是（完全）同步.本书只是在线性多个体系统语义下，用弱一致代替同步，同步则用于耦合的非线性系统网络中.

（3）复杂网络的稳定性控制.这是一类特殊协调性行为，即网络中所有节点收敛到与网络节点初值无关的状态（轨道）.其定义如下.

定义1.3 如果所有节点的状态满足

其中，s（t）可以是未耦合系统（t）=f（s（t），t）的一个平衡点、周期轨道，甚至包含混沌等奇异吸引子，则称网络稳定（同步）到目标轨道s（t）.

系统的稳定性在控制理论中也有大量的研究.本书将着重于如何在复杂网络中实现稳定性控制.而且，控制节点具有局部化分布，即只要在部分节点上设置稳定控制器.此类稳定性控制称之为牵引控制（pinning control[48，49]）.

实现协调性，不同个体间必须存在信息交流.这些信息交流可以是有向的，也可以是无向的.每个个体根据来自其他个体的信息调整自身的状态，从而最终实现同步或一致.这些相互之间存在信息交流的所有个体就构成了一个复杂网络，其结构仍然可以用一个图来描述，它的节点表示其中的每个个体.如果两个个体之间有信息交流关系，则在它们之间连一条边，有向边表示有向的信息流，而无向边则表示双向的信息流.如果各个个体之间的关系不随时间而变化，则网络具有一个静态的结构.而在有些情形下，个体之间的关系却会随时间而变化.这主要是由于不可靠的信息传输、有限的通信或感知半径，再加上个体之间位置变化以及其他原因造成的.而且，有时个体的状态更新规则也会随时间而变化（[50]）.这时系统就有一个动态的网络结构.在动态网络结构中有一种比较重要的类型就是所谓的切换结构.此时，网络的结构会在一些确定或者不确定的时间点上发生跳变.跳变所产生的新的网络结构既可能是确定性的，也有可能是随机的.

线性耦合常微分方程（LCODEs）是一类用以描述耦合的连续时间系统的模型.作为一个理论模型，在时空复杂网络和复杂系统有广泛的研究（参见文献[53，54]）.线性耦合常微分方程中每个节点的动力学行为有两个机制控制：一是自身的非线性的动力学结构；另一个是与之连接的节点对其的扩散影响.LCODEs的一般形式可以描述如下：

设aii=-，则系统可改写为

其中xi（t）∈ℝn表征第i节点的状态变量，t∈[0，+∞）是连续时间，f：ℝn×[0，+∞）→ℝn是一个连续函数，A=（aij）∈ℝm×m称为耦合矩阵，aij≥0可决定节点j对i的耦合权重，i≠j，Γ=diag{γ1，γ2，…，γn}，γi≥0，i=1，…，n.

由于节点间信号传输速度的有限性，以及节点对于信号处理时间的消耗，通讯时滞不可避免.此时，方程（1.6）变为

这里τij表示从节点j到i的通讯时滞，其中τii描述节点处理自身信号的时间.当τii=0，上述方程可写为

特别地，τij=τ对任意i，j都成立，表示时滞是一致的.我们也考虑τij随时间变化（即τij（t））的情形.当f=0和Γ=I，方程（1.7）变为

这也是具有时滞的多智能体一致性算法.其离散时变情形下，可写为如下差分方程形式：

假设τij≤τM对任意i，j成立，上式也可写为如下一般增广形式：

在此基础上，牵制可加在某些（少量）节点集合（记为D）上，用以将多智能体系统稳定到实现给定的平衡点上：

这里，τi描述牵制项的时滞.当然本书也考虑耦合系数aij随时间变化（即aij（t））的情形.