电励磁同步发电机的分析和优化

8.2.4.1　隐极式同步发电机

1.不计磁饱和时

同步发电机负载运行时，除了主极磁动势之外，还有电枢磁动势。如果不计磁饱和（即认为磁路为线性），则可应用叠加原理，把和的作用分别单独考虑，再把它们的效果叠加起来。设和各自产生主磁通和电枢磁通，并在定子绕组内感应出相应的励磁电动势和电枢反应电动势，把和相量相加，可得电枢一相绕组的合成电动势（亦称为气隙电动势）。上述关系可表示为

再把合成电动势减去电枢绕组的电阻压降和漏抗压降（Xσ为电枢绕组的漏电抗），便得电枢绕组的端电压。采用发电机惯例，以输出电流作为电枢电流的正方向时，电枢的电压方程为

因为电枢反应电动势正比于电枢反应磁通，不计磁饱和时，又正比于电枢磁动势和电枢电流，即

Ea∝Φa∝Fa∝I

因此正比于；在时间相位上，滞后于90°电角度，若不计定子铁耗，与同相位，则将滞后于90°电角度。于是亦可写成负电抗压降的形式，即

式中　Xa——与电枢反应磁通相应的电抗，称为电枢反应电抗。

将式（8-12）代入式（8-11），可得

式中　Xs——隐极同步电机的同步电抗，Xs=Xa+Xσ，它是对称稳态运行时表征电枢反应和电枢漏磁这两个效应的一个综合参数。不计饱和时，Xs是一个常值。

图8-15表示与式（8-11）和式（8-13）相对应的相量图，图8-16表示与式（8-13）相应的等效电路。从图8-16可以看出，隐极同步发电机的等效电路由励磁电动势和同步阻抗Ra+j　Xs串联组成，其中表示主磁场的作用，Xs表示电枢反应和电枢漏磁场的共同作用。

图8-15　隐极同步发电机相量图

2.考虑磁饱和时

考虑磁饱和时，由于磁路的非线性，叠加原理不再适用。此时，应先求出作用在主磁路上的合成磁动势，然后利用电机的磁化曲线（空载曲线）求出负载时的气隙磁通及相应的气隙电动势，即

图8-16　隐极同步发电机的等效电路

再从合成电动势减去电枢绕组的电阻和漏抗压降，得电枢的端电压，即

或

相应的考虑磁饱和时隐极同步发电机相量图如图8-17所示，考虑磁饱和时隐极同步发电机合成磁动势与合成电动势E间的关系如图8-18所示。图8-16中既有电动势相量，又有磁动势矢量，故称为电动势-磁动势图。

图8-17　考虑磁饱和时隐极同步发电机相量图

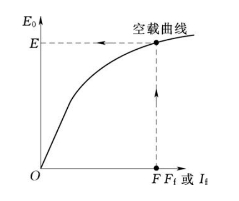
图8-18　考虑磁饱和时隐极同步发电机F-E关系图

8.2.4.2　凸极式同步发电机

凸极同步电机的气隙沿电枢圆周分布不均匀，因此在定量分析电枢反应的作用时需要应用双反应理论。

1.双反应理论

凸极同步电机的气隙不均匀，极面下气隙较小，两极之间气隙较大，故直轴下单位面积的气隙磁导λd要比交轴下单位面积的气隙磁导λq大很多。当正弦分布的电枢磁动势作用在直轴上时，由于λd较大，故在一定大小的磁动势下，直轴基波磁场的幅值Bad1相对较大。当同样大小的磁动势作用在交轴上时，由于λq较小，在极间区域交轴电枢磁场出现明显下凹，相对来讲，基波幅值Baq1将显著减小。

不失一般性，当电枢磁动势在空间任意位置（既不在直轴、亦不在交轴）时，可把电枢磁动势分解成直轴和交轴两个分量(www.xing528.com)

再用对应的直轴磁导和交轴磁导分别算出直轴和交轴电枢反应，最后把它们的效果叠加起来。这种考虑到凸极电机气隙的不均匀性，把电枢反应分成直轴和交轴电枢反应分别来处理的方法，就称为双反应理论。利用双反应理论得到凸极同步发电机各电磁量之间的关系为

实践证明，不计磁饱和时，这种方法的效果是令人满意的。

在凸极电机中，直轴电枢磁动势Fad和交轴电枢磁动势Faq换算到励磁磁动势时，分别应乘以直轴和交轴换算系数kad和kaq。

2.电压方程和相量图

不计磁饱和时，根据双反应理论，把电枢磁动势分解成直轴和交轴磁动势、，分别求出其所产生的直轴、交轴电枢磁通、和电枢绕组中相应的电动势、，再与主磁通所产生的励磁电动势相量相加，得一相绕组的合成电动势（通常称为气隙电动势）。再从气隙电动势减去电枢绕组的电阻和漏抗压降，便得电枢的端电压。采用发电机惯例，电枢的电压方程为

与隐极电机相类似，由于Ead和Eaq分别正比于相应的Φad、Φaq，不计磁饱和时，Φad和Φaq又分别正比于Fad、Faq，而Fad、Faq又正比于电枢电流的直轴和交轴分量Id、Iq，于是可得

Ead∝Id，Eaq∝Iq

其中　Id=Isinψ0，Iq=Icosψ0

在时间相位上，不计定子铁耗时，和分别滞后于、90°电角度，所以和可以用相应的负电抗压降表示为

式中　Xad——直轴电枢反应电抗；

Xaq——交轴电枢反应电抗。

将式（8-16）代入式（8-15），并考虑到，可得

式中　Xd、Xq——直轴同步电抗和交轴同步电抗，它们是表征对称稳态运行时电枢漏磁和直轴或交轴电枢反应的一个综合参数。

式（8-17）就是凸极同步发电机的电压方程。图8-19为凸极同步发电机的相量图。

图8-19所示相量图比较复杂，由式（8-17）不能直接画出来，除需给定端电压、负载电流、功率因数角cosφ以及电机的参数Ra、Xd和Xq之外，必须先把电枢电流分解成直轴和交轴两个分量，为此须先确定ψ0角，或者说先求的方向，详见文献［1］。

图8-19　凸极同步发电机的相量图（以为参考方向）

图8-19是凸极同步发电机以电压为参考方向的相量图形式。以空载电动势为参考方向的相量图如图8-20所示。

图8-20　为凸极同步发电机的相量图（以为参考方向）

3.直轴和交轴同步电抗的意义

由于电抗与绕组匝数的平方和所经磁路的磁导成正比，所以有

其中　Λd=Λad+Λσ，Λq=Λaq+Λσ

式中　N1——电枢每相的串联匝数；

Λd、Λq——稳态运行时直轴和交轴的电枢等效磁导；

Λad、Λaq——直轴和交轴电枢反应磁通所经磁路的磁导；

Λσ——电枢漏磁通所经磁路的磁导。

如图8-21所示。对于凸极电机，由于直轴下的气隙比交轴下气隙小，Λad＞Λaq，所以Xad＞Xaq，因此在凸极同步电机中，Xd＞Xq。对于隐极电机，由于气隙是均匀的，故Xd≈Xq≈Xs。

图8-21　凸极同步电机电枢磁通和漏磁通所经磁路及其磁导