双馈风力发电系统优势明显,因而获得广泛应用,然而,定子和电网直接连接的结构使得双馈风力发电系统对电网电压故障非常敏感。最初,电网发生故障时,双馈风力发电系统立即与电网解列以保护其自身硬件,但随着风电比重不断增加,电网对风力发电系统的运行制定了更严格的标准。紧急电网运行规程要求风力发电机组在电网故障时不得与系统解列,需承受暂态最大5%,稳态最大2%的电网不对称电压。同时,风能资源丰富的区域多集中于偏远地区,那里处于电网末端,电网网架结构薄弱,电网电压容易出现波动、不对称等异常情况,因此,双馈风力发电系统不对称电网下的运行控制成为了一个非常突出的问题。
根据对称分量理论,不对称的电网电压将在双馈风力发电机(DFIG)中引入负序扰动分量,从而造成转子过流、功率脉动、电磁转矩脉动等一系列问题,带来电气和机械冲击。目前普遍采用的解决方案是正、负序双dq域矢量控制,这种方法以传统矢量控制为基础,能够有效地对正序和负序分量进行控制,但双PI环控制影响了系统的动态性能,负序控制器的加入增加了控制系统的复杂性,在工程应用中还存在控制器矫正参数较多的问题。为此,文献[49]提出一种采用多频点比例积分谐振(MFPIR)控制器控制转子电流内环的方法,省去了负序dq域控制器,但仍然采用双环结构。
文献[50]提出一种基于MFPIR的矢量控制方法,这种方法在正序同步坐标系中对定子侧功率进行单闭环控制,不需要负序dq域控制器和转子电流内环,控制器结构简单,只需对算法中一个简单参数(λ∈[0,2])进行调整,即可以以统一的控制结构实现不对称电网电压下双馈风力发电系统的多目标控制,该方法也适用于双馈系统不对称低电压穿越的控制。下面给出采用多频点比例积分谐振(MFPIR)进行双馈系统不对称低电压穿越的控制的仿真结果,详细内容请读者参考文献[45]、[47]。
基于MATLAB/Simulink环境,搭建1.5MW双馈风力发电系统的仿真平台,其中DFIG系统及仿真相关参数见表4-8。变换器开关频率2kHz在不同电网电压和λ取值条件下(λ∈[0,2]),系统的仿真结果如图4-36~图4-38所示。注意,采用不对称度(AF)来表征电网电压或电流的不对称程度,其定义为负序分量占正序分量的比例。
表4-8 DFIG系统仿真参数
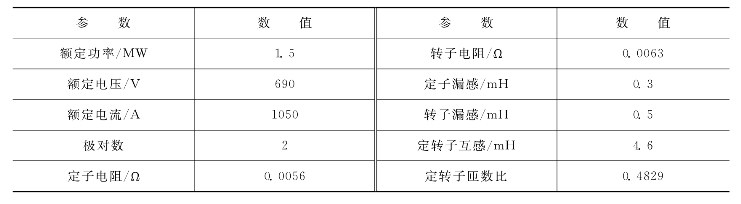
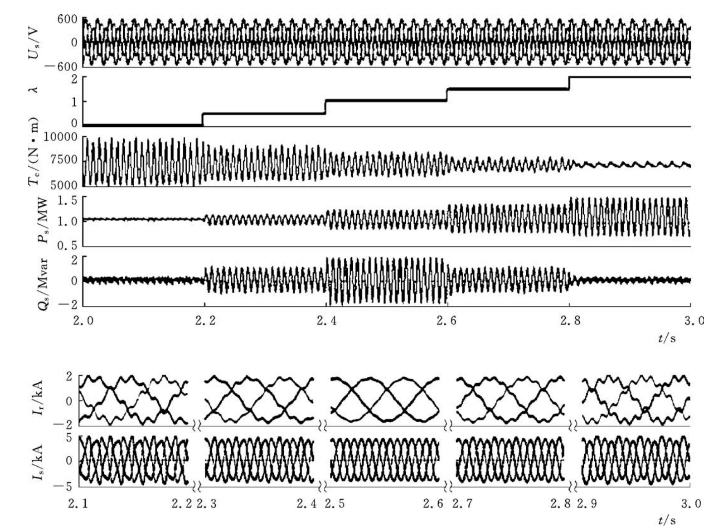
图4-36为不对称电网电压下双馈风力发电系统各种控制目标相互切换的动态过程。可见,通过简单地修改λ参数,系统能够在多个控制目标间实现实时切换,满足不同工况、不同用户的要求,且切换过程平滑、动态响应迅速。
图4-37为各种不对称电压条件下,λ参数设定与系统稳态特性的关系图。由图4-37可知,当控制目标分别被设置为有功和无功功率稳定(λ=0)、定子电流正弦且对称(λ=1)、电磁转矩和无功功率稳定(λ=2)时,控制目标量中的脉动被有效抑制,其控制效果和理想电网条件下近乎一致,而此时,非控制目标量的脉动将会较大。由图中还可看出,控制目标Ⅰ&Ⅱ和Ⅲ彼此相互排斥,有功脉动较小时,转矩脉动较大,两者折中时无功脉动却较大,因此三者脉动都较小的情况不可同时获得,但是通过调节λ的数值,可在不同控制目标之间取得一种折中,即控制目标Ⅳ。
 (https://www.xing528.com)
(https://www.xing528.com)
图4-36 多目标控制的动态特性(电网电压不对称度15%)
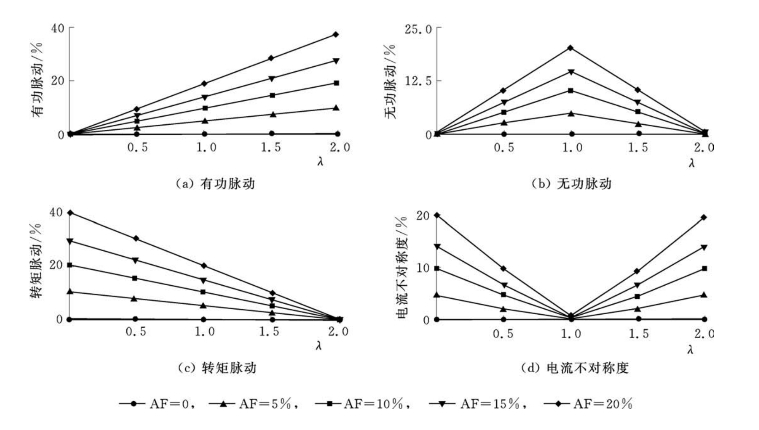
图4-37 系统在各种工况和λ参数下的稳态特性
图4-38为定子电流的谐波分析。可以看到,当λ≤1时,各种不同工况下,定子电流的谐波畸变率(THD)随λ增加而减小,即定子电流波形愈发趋向正弦波;当λ>1时,定子电流的THD都较低,且和理想电网条件下定子电流的控制效果非常接近,这表明此时定子电流的正弦度已经非常高,但随着λ的取值增加,定子电流的三相不对称度逐渐增加(图4-36和图4-37)。由此可知,电流的负序分量在时域波形上表现在两个方面,即波形的正弦度和波形的对称度,且当λ=1时,定子电流负序分量最低,波形质量达到最优。
上述方法能够用于DFIG的不对称低电压穿越控制,图4-39为电网电压发生500ms不对称电压跌落(AF=20%)时的低电压穿越过程。由图4-39可见,在电网电压故障发生75ms后,有功功率降额输出、并向电网注入无功功率400kvar以支撑电网;在电网电压恢复75ms后系统恢复有功功率输出,并实现单位功率因数。整个低电压过程中,双馈风力发电系统与电网保持连接,并为电网提供无功支撑,有效实现低电压穿越。
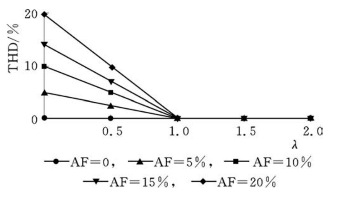
图4-38 定子电流谐波分析
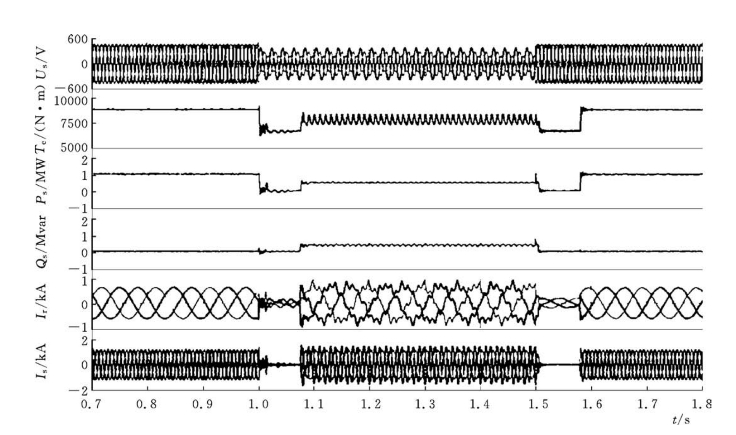
图4-39 不对称低电压穿越控制的仿真结果(电网电压不对称度20%,λ=0)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




