DFIG无功特性分析与调节机制验证

1.仿真参数与过程

针对1.5MW机组，采用Matlab/Simulink进行仿真算例验证，见表4-5。仿真时间为20s，包括并网及最大功率点追踪（Maximum Power Point Tracing，MPPT）。发电机0.5s并网，并网后风速为6m/s，10s时风速跃变为9m/s。

表4-5　仿真风力发电机参数

图4-17为发电机定子电流i1和转子电流i2仿真波形，图4-18为发电机转速n和定子有功功率P1仿真波形。并网后发电机先后对2种风速进行MPPT，实现了从亚同步到超同步的全过程仿真，基于此可分析转差率对DFIG无功特性的影响。为了便于研究，本书根据两种风速下稳态MPPT（亚同步稳态和超同步稳态）时段的仿真数据进行定量分析。两种风速下稳态MPPT时段的基本数据见表4-6。

图4-17　发电机定子电流i1和转子电流i2仿真波形

图4-18　发电机转速n和定子输出有功功率P1仿真波形

表4-6　不同风速下的稳态MPPT结果

2.仿真算例分析

除了考虑转差率影响因素外，为同时分析定子无功功率输出对转子无功功率的影响，分别设定4种定子无功指令：①0var；②600kvar；③-200kvar；④-600kvar。图4-19～图4-22分别为4种情况下定、转子无功功率仿真结果。由于实现了功率解耦，各情况下的n和P1变化规律均如图4-18所示。(www.xing528.com)

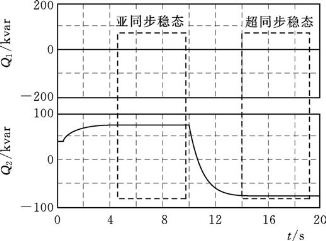
图4-19　定子无功功率Q1和转子无功功率Q2=0kvar）

图4-20　定子无功功率Q1和转子无功功率Q2=600kvar）

图4-21　定子无功功率Q1和转子无功功率Q2=-200kvar）

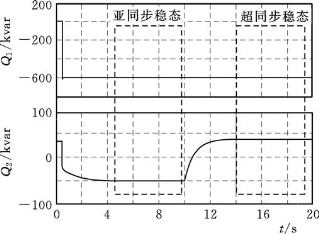
图4-22　定子无功功率Q1和转子无功功率Q2=-600kvar）

图4-19可用于分析DFIG定、转子无功折算关系和调节机制。由电机参数仿真算得其额定励磁功率Qm≈360kvar，如果Qm全部由定子侧提供，DFIG需要从电网输入无功功率Q1≈360kvar。由于=0，Qm全部由转子无功功率Q2提供，即Q2与定子无功功率Q1=360kvar具有相同效能。即虽然图4-19中Q2与转速有关，但Q2按式（4-55）折算后应该与360kvar相等。由表4-6和图4-19可知，亚同步稳态时段和超同步稳态时段的s分别为0.2和-0.2，Q2分别为72.6kvar和-73kvar，折算后分别为363kvar和365kvar，与360kvar非常接近。存在少量误差的原因是没有计及漏感消耗的无功功率。通过算例可知，DFIG以小额转子无功功率（72.6kvar和73kvar）满足了励磁无功功率需求（360kvar），与定子侧输入360kvar的无功功率是等效的。验证了4.4.2中关于DFIG定子、转子无功折算关系及调节机制分析的正确性。

图4-20～图4-22反映了转差率和定子无功对转子无功的影响规律。

图4-20中，=600kvar＞0。亚同步稳态时段s=0.2＞0，Q2=220kvar＞0；超同步稳态时段s=-0.2＜0，Q2=-220kvar＜0。即定子输出感性无功时，Q2仅与s有关，验证了4.4.2中DFIG无功特性分析部分结论的正确性。

图4-21、图4-22为＜0的情况。由4.4.2中DFIG无功特性分析之（3）中3）、4）部分可知，此时Q2不但与s有关，还与定子无功Q1有关，现以亚同步稳态时段为例进行验证。由表4-6知该时段P1=278.5kW，由式（4-60）解得Q1a=-327kvar，Q1b=-5139kvar。图4-21中=-200kvar＞Q1a，由图可知，亚同步稳态时段Q2=23kvar＞0。图4-22中Q1b＜=-600kvar＜Q1a，亚同步稳态时段时段Q2=-52kvar＜0。图4-21、图4-22亚同步稳态时段仿真结果表明，当s＞0时，除s外Q2还取决于Q1，验证了4.4.2中DFIG无功特性分析之（3）中3）部分结论的正确性。类似地，利用图4-21、图4-22中超同步稳态时段的仿真结果也可证明4.4.2中DFIG无功特性分析之（3）中4）部分结论的正确性。