DFIG无功功率机制及特性分析

1.DFIG等效电路和无功平衡方程

图4-14为采用发电机惯例的DFIG等效电路。根据等效电路，可列方程（忽略rm）为

图4-14　双馈型异步发电机等效电路

式中　——定、转子电压相量；

——气隙磁场感应电动势相量；

——定子、转子电流和励磁电流相量；

r1、r2——定子、转子电阻；

X1σ、X2σ、Xm——定子、转子漏抗和互抗，记X1=X1σ+Xm，X2=X2σ+Xm，转子各量均已折算到定子侧；

s——DFIG转差率。

为方便，将定子电压、电流相量写为

式中　——基准相量；

U1——的有效值；

I1x、I1i——定子电流的有功分量和无功分量。

将式（4-44）代入式（4-43）中可得

转子电流的有效值为

DFIG定子、转子无功功率分别为

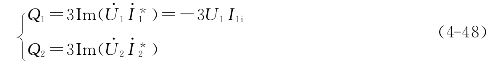
式中　Q1——定子无功功率；

Q2——转子无功功率。

根据图4-16的电流方向，式（4-48）中无功符号定义为：Q1＞0（＜0）表示定子输出（输入）感性无功功率；Q2＞0（＜0）表示转子输入（输出）感性无功功率。由式（4-43）中的第3式可得

由式（4-45）～式（4-49）可推得

即

式中　Qx1σ、Qx2σ、Qm——定子、转子漏感消耗的无功功率和气隙励磁功率。

则式（4-50）可写为

记

式中　Qm1、Qm2——定、转子励磁功率。

则有

式（4-52）、式（4-53）为DFIG的无功关系方程，方程中存在“s因子”，定子、转子无功功率不满足守恒定律，其根本原因是定子、转子侧频率不相同。

2.定子、转子的无功折算及调节机制(www.xing528.com)

相对于DFIG的有功功率，其无功功率的影响因素较多，特性更为复杂。定子、转子频率差异导致定子、转子无功功率不能直接等效（即不满足守恒定律），而DFIG具有独特而灵活的无功调节能力。分析不同频率下的定子、转子无功折算关系和无功调节机制是深入研究DFIG无功特性的前提和基础。

有功（电阻）与频率无关，而无功（电抗）与频率有关，不同频率定子、转子回路的无功功率必须经过折算才能满足守恒定律，式（4-52）、式（4-54）中的转差率s体现了这个特点。设Q2、Qm2、Qx2σ折算到定子侧后分别为，则有

由式（4-55）可知，由于DFIG定、转子侧的频率分别为f1（工频）和sf1，转子无功折算到定子侧将被放大1/s倍。根据本节无功定义，Q1为定子输出（感性）无功功率，Q2为转子输入（感性）无功功率，二者分别为DFIG定子、转子侧的实际物理量。但定子、转子不同频率使Q1、Q2不能直接等效。类似于电机学中转子阻抗向定子侧的频率折算，Q2也需通过频率折算等效到定子侧。其折算值Q′是一虚拟量，物理意义为工频50Hz下的等效转子无功当量。

同一转子无功功率在亚同步（s＞0）和超同步（s＜0）情况下被等效到定子侧后将呈现不同的性质（感性或容性）。相反，当要求定子无功输出恒定时，变换器向转子输出无功功率的大小和性质（感性或容性）将随着转速而变化。以小额转子无功功率等效大额定子无功功率，这是DFIG灵活、强大无功调节能力的内在机制。

计及折算关系后，根据式（4-52）、式（4-54）可得到频率折算后的DFIG无功平衡方程为

式（4-56）和式（4-57）中不再有“s因子”，表明折算后的转子无功功率与定子无功功率满足常规的守恒定律。

3.DFIG无功特性分析

基于定子、转子无功折算关系和调节机制可进一步分析DFIG的无功特性，即不同转速下的定子、转子无功关系（包括内部无功潮流）。通过辨证分析转差率、定子无功功率、转子无功功率之间的相互影响规律总结不同运行工况下的DFIG无功特性，如图4-15所示。

图4-15　DFIG的无功功率

（1）转差率和定子无功功率对转子无功的影响规律。根据DFIG的转速和定子无功功率的不同性质，分下述4种情况讨论转子无功特性。由前面讨论可知Qx1σ、、Qm恒大（等）于零，均为（消耗的）感性无功功率。

1）Q1＞0，s＞0（定子输出感性无功，亚同步运行）。当s＞0、Q1＞0时，由式（4-56）可知，＞0，由式（4-55）得Q2=＞0。根据本书无功符号规定，DFIG亚同步运行且定子输出感性无功功率时，转子输入感性无功功率，此时DFIG无功特性如图4-15（a）所示。

2）Q1＞0，s＜0（定子输出感性无功功率，超同步运行，类似于1），此时＞0，Q2=＜0，即超同步运行且定子输出感性无功功率时，转子输出感性无功功率。此时DFIG无功特性如图4-15（b）所示。

3）Q1＜0，s＞0（定子输入感性无功功率，亚同步运行）。当Q1＜0时，的正负不能简单确定，需要进一步分析。将式（4-56）展为关于Q1的函数

其中，系数a、b、c为

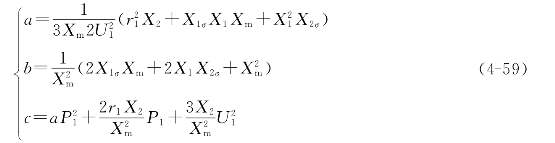
式（4-58）为关于Q1的二次方程，可据此分析Q1与的关系。DFIG定子、转子无功关系曲线如图4-16所示。当b2-4ac＜0时方程无零解，此时＞0，Q2=＞0，转子输入感性无功功率。此时DFIG无功特性如图4-15（c）所示。

当b2-4ac≥0时，方程有零解，其解为

Q1与的关系如图4-16（b）所示，的正负与Q1有关：Q1≤Q1b或Q1≥Q1a时，≥0，Q2=≥0，无功特性如图4-15（c）所示；Q1b＜Q1＜Q1a时，＜0，Q2=＜0，转子输出感性无功功率，无功特性如图4-15（d）所示。

4）Q1＜0，s＜0（定子输入感性无功功率，超同步运行）。分析方法类似情况3），由于s＜0，Q2的正负与相反。当b2-4ac＜0时＞0，Q2=＜0，转子输出感性无功功率，DFIG无功特性如图4-15（e）所示。当b2-4ac≥0时，的正负与Q1有关：Q1≤Q1b或Q1≥Q1a时，≥0，Q2=≤0，无功特性如图4-15（e）所示；Q1b＜Q1＜Q1a时，＜0，Q2=＞0，转子输入感性无功功率，无功特性如图4-15（f）所示。

DFIG转差率和定子无功功率对转子无功功率的影响规律可总结如下：当定子输出感性无功功率（Q1＞0）时，转子无功功率的性质仅与转速有关：亚同步运行（s＞0）时，转子输入感性无功功率；超同步运行（s＜0）时，转子输出感性无功功率。当定子输入感性无功功率（Q1＜0）时，转子无功特性较复杂，与s与Q1均有关系。

（2）转差率和转子无功对定子无功功率的影响规律。由式（4-56）可以得到

将式（4-51）、式（4-55）代入式（4-61）得到

其中　根据式（4-62）可分析不同工况下定子无功特性。

1）Q2＞0，s＞0（转子输入感性无功功率，亚同步运行）。当Q2＞sQ∑时，Q1＞0，定子输出感性无功功率，此时DFIG无功特性如图4-15（a）所示；当0＜Q2＜sQ∑时，Q1＜0，定子输入感性无功功率，此时DFIG无功特性如图4-15（c）所示。

2）Q2＞0，s＜0（转子输入感性无功功率，超同步运行）。此时恒有Q1＜0成立，定子输入感性无功功率，此时DFIG无功特性如图4-15（f）所示。

3）Q2＜0，s＞0（转子输出感性无功功率，亚同步运行）。此时恒有Q1＜0成立，定子输入感性无功功率，此时DFIG无功特性如图4-15（d）所示。

4）Q2＜0，s＜0（转子输出感性无功功率，超同步运行）。当Q2＜sQ∑时，Q1＞0，定子输出感性无功功率，此时DFIG无功特性如图4-15（b）所示；当sQ∑＜Q2＜0时，Q1＜0，定子输入感性无功功率，此时DFIG无功特性如图4-15（e）所示。

图4-16　DFIG定子、转子无功关系曲线

DFIG转差率和转子无功功率对定子无功功率的影响规律可总结如下：当转子输入感性无功功率（Q2＞0）且发电机超同步运行（s＜0）时，或者转子输出感性无功功率（Q2＜0）且发电机亚同步运行（s＞0）时，定子输入感性无功功率；其他情况下定子无功特性稍复杂，与s和Q2均有关系。

本部分所分析的运行工况对转子无功功率的影响和对定子无功功率的影响是相互辨证且本质统一的，是DFIG无功特性在不同角度的体现。综合两方面的分析可得到图4-15所示的DFIG 6种无功特性。