两相静止与旋转的变换方法（2S/2R变换）

两相静止绕组α、β通以两相平衡交流电流，产生旋转磁动势。如果令两相绕组转起来，且旋转角速度等于合成磁动势的旋转角速度，则两相绕组通以直流电流就产生空间旋转磁动势。图3-11中绘出两相旋转绕组d和q，从两相静止坐标系αβO到两相旋转坐标系dqO的变换，称作两相静止—两相旋转变换，简称2S/2R变换，其中S表示静止，R表示旋转，变换的原则同样是产生的磁动势相等。

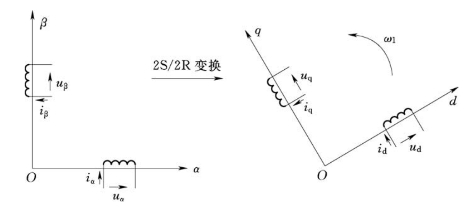
图3-11　静止两相坐标系到旋转两相坐标系变换

旋转变换矢量关系如图3-12所示，is为定子电流空间矢量，图中dq坐标系是任意同步旋转坐标系，旋转角速度为同步角速度ω1。由于两相绕组α、β在空间上的位置是固定的，因而d轴和α轴的夹角φ随时间而变化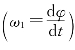，在矢量变换控制系统中，φ通常称为磁场定向角。

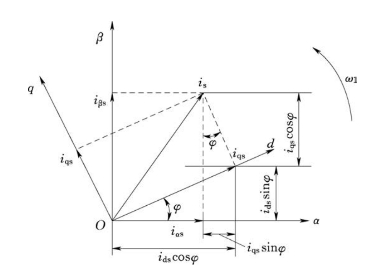
图3-12　旋转变换矢量关系图

由图3-12可以看出

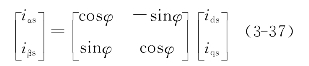
令

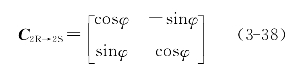
式（3-38）即为由两相同步旋转坐标系到两相静止坐标系的矢量旋转变换矩阵。(www.xing528.com)

由于变换矩阵C2R→2S是一个正交矩阵，所以。因此由静止坐标系变换到同步旋转坐标系的矢量变换方程式为

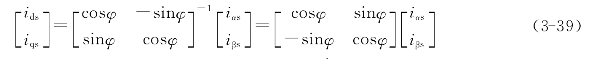
令

式（3-40）即为两相静止坐标系到两相同步旋转坐标系的矢量旋转变换矩阵。

仿照定子两相同步旋转坐标系到两相静止坐标系的矢量旋转变换，可以得到转子两相旋转坐标系d′q′到两相静止坐标系的坐标变换过程为

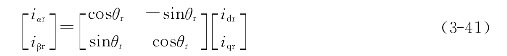
式中　idr、iqr——转子两相旋转dq坐标系的电流；

iαr、iβr——两相静止坐标系下的电流；

θr——转子转过的空间电角度。