三相静止与两相静止变换（3S/2S变换）

三相异步电动机动态模型相当复杂，分析和求解这组非线性方程十分困难。在实际应用中必须予以简化，简化的基本方法就是坐标变换。异步电动机数学模型之所以复杂，关键是因为有一个复杂的6×6电感矩阵，它体现了影响磁链和受磁链影响的复杂关系。因此，要简化数学模型，须从简化磁链关系入手。

在三相绕组A、B、C和两相绕组α、β之间的变换，称为三相坐标系和两相坐标系间的变换，简称3S/2S变换。

图3-10中绘出了A、B、C和α、β两个坐标系中的磁动势矢量，将两个坐标系原点并在一起，使A轴和α轴重合。设三相绕组每相有效匝数为N3，两相绕组每相有效匝数为N2，各相磁动势为有效匝数与电流的乘积，其空间矢量均位于相关的坐标轴上。

当两者的旋转磁场完全等效时，合成磁动势沿相同轴向的分量必定相等，即三相绕组和两相绕组的瞬间磁动势沿α、β轴的投影相等，即

图3-10　三相定子绕组与两相定子绕组磁势的空间位置

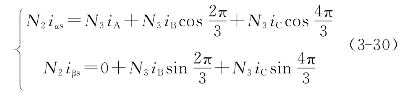
经计算并整理后，用矩阵表示为

简记为i=C3S→2Si。

为求其逆变换，引入另一个独立于iαs、iβs的新变量i0，称之为零序电流，并定义

(www.xing528.com)

式中　K——待定系数。

对两相系统而言，零序电流是没有意义的，这里只是为了纯数学上求逆的需要而补充定义的一个值为零的零序电流（相应坐标系才称为αβO坐标系）。需要说明的是，这并不影响总的变换过程。

式（3-31）和式（3-32）合并后，C3S→2S成为

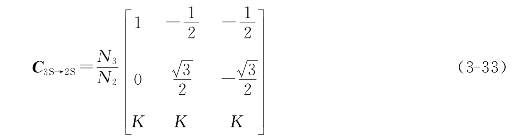
将C3S→2S求逆，得到

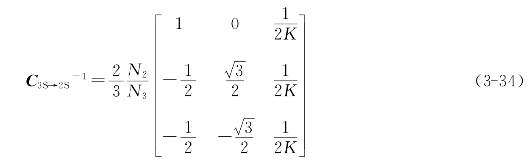
根据等功率原则，要求。［用到矩阵的运算公式（AB）T=BTAT］据此，经过计算整理可得

于是

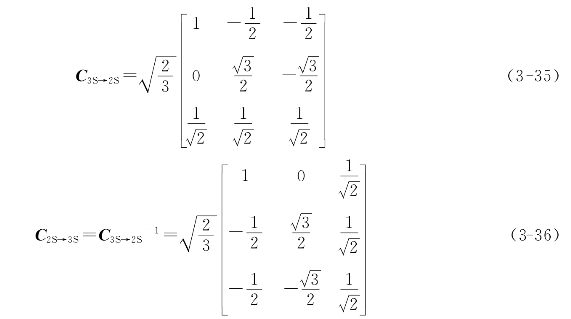
式（3-35）和式（3-36）即为定子三相/两相静止坐标系变化矩阵，以上两式同样适用于定子电压和磁链的变化过程。需要注意的是，当把以上两式运用于转子坐标系的变换时，变换后得到的两相坐标系和转子三相坐标系一样，相对转子实体是静止的，但是，相对于静止的定子坐标系而言却是以转子角频率ωr旋转的。因此和定子部分的变换不同，转子部分实际上是三相旋转坐标系变换成两相旋转坐标系。