单相绕组的脉振磁动势探究

2.3.2.1　线圈的磁动势

组成绕组的单元是线圈，下面先分析一个线圈所产生的磁动势。

图2-9所示为一个整距线圈的磁动势示意图及波形图。定子上只有一个整距线圈AX，该线圈放置在水平轴线上，其匝数为Nc，当电流i从X流入，从A流出时，线圈产生的磁势为Nci，磁力线的路径遵循右手螺旋定则，如图中虚线所示，由定子铁芯进入气隙为N极，由气隙进入定子铁芯为S极。根据磁场的分布、电流的数值、导线的位置，可确定线圈磁动势的大小及分布。由于不考虑铁芯中磁压降，所以线圈的磁动势降落在两个均匀的气隙中，则气隙各处的磁压降均等于线圈磁动势的一半，即。

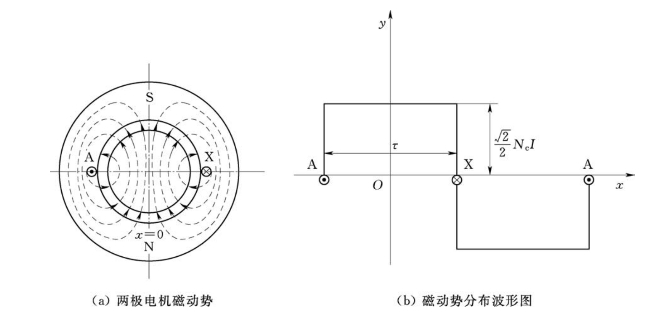
图2-9　一个整距线圈的磁动势

假设将电机定子从放置线圈边A的位置切开并沿气隙圆周展开，如图2-9（b）所示，将定子内圆圆周展成的直线作为x轴，表示气隙圆周所对应的电角度；将磁极轴线确定为y轴，表示磁动势的大小和极性。设N极磁极为正，S极磁极为负，可得整距线圈产生的磁动势沿气隙圆周的分布。设线圈中流过的电流随时间按余弦规律变化，即i=，当ωt=0时，。总磁动势为，不计铁芯磁压降，每侧气隙磁压降各占总磁动势，此时，图2-9（b）所示的磁动势曲线的数学表达式为

由于线圈中流过的电流按正弦规律变化，因此，整距线圈每极磁动势的幅值也随时间按正弦规律变化，其数学表达式为

式中　Fym——矩形波磁动势的幅值，。

上述分析表明：当正弦交流电流通过整距线圈时，所产生的磁动势在空间上是矩形波分布，即每一极下各点的磁势在同一时刻是相等的；而矩形波的高度，即磁动势的大小是随时间按正弦规律变化的，随电流的大小变化而变化，磁动势的极性也随着电流方向的改变而变化。不同瞬间的磁动势脉动分布情况如图2-10所示。把这种空间位置固定，而大小和极性随电流交变的磁动势称为脉振磁动势。其脉振的频率就是线圈中交流电流的频率。

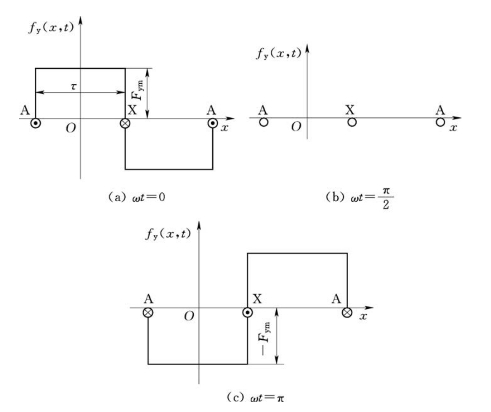
图2-10　不同瞬间整距线圈的脉振磁动势

上述分析是针对一对极的情况进行的。在多极电机中，如果只取一对极内的磁动势来进行分析，则与两极电机的磁动势完全相同。即p对磁极的磁动势分布波形只是在交变次数上较一对磁极的磁动势分布增加p倍而已。图2-11给出了四极电机中电流达到最大值时整距线圈磁动势的分布。

图2-11　两个整距线圈组成的四极磁动势

直接运用矩形波来分析绕组的磁动势是非常不方便的。通常采用傅立叶级数将矩形波分解，根据线圈的基波磁动势得出相绕组的基波磁动势，根据线圈的谐波磁动势得出相绕组的谐波磁动势，最后得出相绕组的合成磁动势。由图2-11可见，整距线圈磁动势是一个对称的矩形波，用傅立叶级数表示为

式中　Fy1——磁动势的基波幅值，；

Fyν——磁动势的ν次谐波幅值，，ν=1，3，5，…。

因此整距线圈所产生的脉振磁动势为

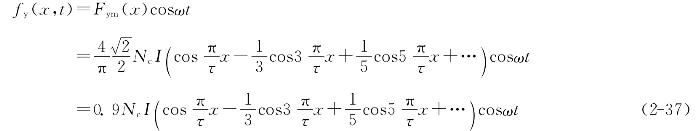
图2-12　不同瞬间整距线圈的脉振磁动势

式（2-37）的矩形波如图2-12所示，为了图面清晰只画了基波和3次、5次谐波。

2.3.2.2　线圈组的磁动势

1.整距分布线圈组

设有q个相同的整距线圈相串联组成一个线圈组。各线圈在空间依次相距α电角度，若各线圈的匝数相等，流过的电流也相同，便产生q个振幅相等的矩形磁动势波，但空间依次相距α电角度。整距线圈的线圈组磁动势如图2-13所示。q=3，α=20°，共有3个高度相等的矩形波，彼此相差20°。利用傅氏级数把每一个矩形磁动势波分解成基波及一系列奇次谐波。图2-13（b）中的曲线1、2、3分别代表3个幅值相等、在空间互差20°电角度的整距线圈的基波磁动势。若把这3个基波磁动势逐点相加，就可得到基波合成磁动势（曲线4），其振幅为Fq1。对各次谐波也可以用逐点相加的方法得到各次谐波的合成磁动势，其振幅为Fqν。

在数学分析上，正弦分布波可用空间矢量来表示，矢量的长度表示振幅，图2-13（b）中3个线圈的基波磁动势分别是3个大小相等，彼此相差20°电角度的空间矢量，按矢量相加，其合成磁动势基波即为这3个线圈矢量的矢量和，如图2-13（c）所示，这个矢量和比各线圈的代数和小。

以上分析与线圈组基波电动势的合成相似，因此同样可以引入分布因数Kd1来计及线圈分布的影响。故线圈组磁动势的基波振幅为

图2-13　整距线圈的线圈组磁动势

式中　qNc——每线圈组的匝数；

Kd1——磁动势的基波分布因数，计算公式与电动势的基波分布因数公式相同，见式（2-17）。

同理，线圈组磁动势的ν次谐波振幅为

式中　Kdν——磁动势的ν次谐波分布因数，计算公式与电动势的ν次谐波分布因数公式相同，见式（2-26）。

【例2-3】　三相四极交流电机，定子槽数Z=36，计算其基波和5次谐波磁动势的分布因数。

【解】(www.xing528.com)

槽距角为

每极每相槽数为

基波分布因数为

5次谐波分布因数为

7次谐波分布因数为

由此例可以看出，5次、7次谐波分布因数要比基波分布因数小得多，这意味着采用分布绕组虽然会使基波合成磁动势有所减小，但对高次谐波却削弱得更多。因此，采用分布绕组是改善磁动势波形的有效措施之一。

2.短距分布线圈组

双层绕组通常是短距绕组，线圈节距缩短后对合成磁动势有一定影响，下面分析短距对线圈组磁动势的影响。

图2-14所示为q=2，的双层短距叠绕组中一对极下同属同一相的两个线圈组。

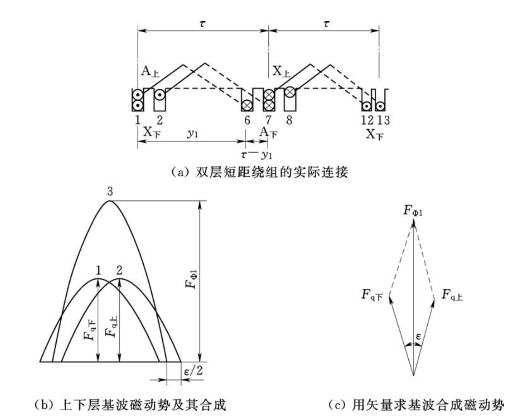
图2-14　双层短距绕组

从产生磁场的观点来看，磁动势既取决于槽内导体电流的大小和方向，又与槽内有效圈边的分布和匝数有关，但与圈边的连接次序无关。因此，为分析方便，仿效单层整距绕组分析方法，分别求出这两个单层整距分布绕组的磁动势，其基波分量为图2-14（b）中的曲线1、2，这两个磁动势的幅值相等，空间相差一个短距角电角度，把这两条曲线逐点相加，可得到合成曲线3。也可以用磁动势矢量来表示，如图2-14（c）所示，与交流绕组的电动势分析方法相似，双层短距分布绕组的基波磁动势比双层整距时小sin90°倍，此倍数就是基波节距因数Kp1，双层绕组磁动势的基波振幅为

式中　2qNc——双层线圈组的每对极匝数；

Kp1——磁动势的基波节距因数，计算公式与电动势的基波节距因数公式相同，见式（2-14）；

Kw1——磁动势的基波绕组因数，Kw1=Kp1Kd1。

同理，磁动势的ν次谐波振幅为

式中　Kpν——磁动势的ν次谐波节距因数，计算式与电动势的ν次谐波节距因数的计算式相同，见式（2-27）；

Kwν——磁动势的ν次谐波绕组因数，Kwν=KpνKdν。

采用短距绕组也可以削弱或者消除磁动势中的高次谐波，改善磁动势波形。

2.3.2.3　单相绕组的磁动势

在弄清线圈和线圈组的磁动势基础上，可推导出相绕组的合成磁动势。

然而需要指出的是：相绕组由分布在各极下的线圈连接而成，一相绕组的磁动势平均作用于各个磁极，书中所指的单相绕组磁动势，不是总磁动势（即不是各极面下磁动势的叠加），而是作用于一对磁极的磁动势。这与相电动势求法不同，电动势是时间相量，相电动势是将各线圈组电动势按线圈组的接线方式（串联或并联）相加而成，而磁动势是空间矢量，把不同空间的各对磁极的磁动势合并起来是没有意义的。

设每相绕组串联匝数为N，每相并联支路数为a，相电流有效值为I，线圈中的电流，即每条支路的电流Ic=I/a。一个相绕组一对极下的基波磁动势幅值所在的轴线即为该相绕组在该对极下的轴线，以一对极考虑，这就是相绕组的轴线。如空间坐标原点取在相绕组轴线处，导体中电流按正弦规律变化，则单相绕组磁动势按照式（2-37）的形式可表示为

式中　Fφ1——相绕组的磁动势基波振幅，Fφ1=0.9；

Fφν——相绕组磁动势的ν次谐波幅值，Fφν=0.9，ν=3，5，7，…。

图2-15给出了不同瞬间单相绕组基波磁动势的波形，由图可以发现：单相绕组的基波磁动势在空间上随x按正弦规律分布，在时间上随ωt按正弦规律脉振。它既是时间的函数，也是空间的函数。但是图2-15中的磁动势在水平方向没有移动，即不能旋转。

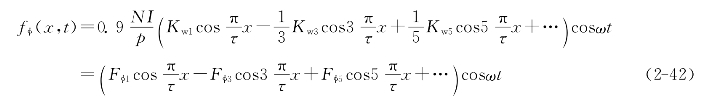
因此，单相绕组流入交流电流时产生脉振磁动势，该磁动势有以下特性：

（1）单相绕组的磁动势是一个在空间位置固定不变，幅值随时间按正弦规律变化的脉振磁动势，基波及所有谐波磁动势的脉振频率都等于绕组中电流的频率。

（2）单相绕组基波磁动势幅值，ν次谐波幅值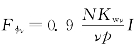。由于Fφν∝Kwν/ν，所以谐波次数越高，幅值越小，绕组分布和适当短距有利于改善磁动势波形。

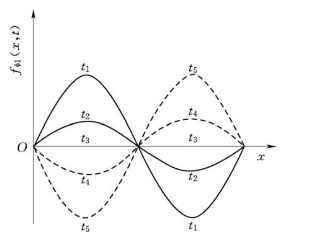
图2-15　不同瞬间时单相绕组的基波磁动势

（3）各对极磁动势只与槽导体电流有关，但把不同空间的磁动势进行合并是没有物理意义的。