材料简化模型的优化策略和方法

根据J2塑性流动等向强化理论，不考虑内层和外层的径向应力、剪切应力和，内层和外层HDPE的本构方程均可用式（22.9）表示［1］：

其中，Dij=φ（σij，Q，υ），i，j=1，2，3；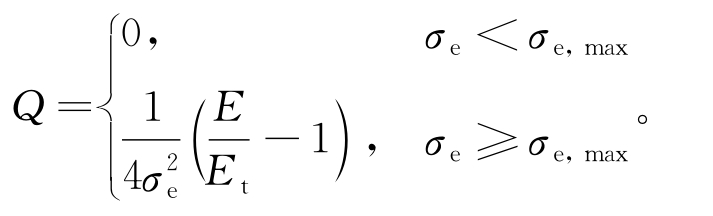

式中　υ——泊松比；

E——弹性模量；

Et——切线模量；

σe——Mises等效应力；

σe，max——最大等效应力。

将玻纤增强柔性管加强层中的HDPE基体和玻璃纤维视为交错布置的螺旋缠绕带结构。复合材料是宏观均匀的，因此研究其力学性能时，只需取其一代表性体积单元即可代表总体进行研究。本节针对玻璃纤维材料各向异性，通过Halpin-Tsai方程求出该层的五个有效模量。

每层玻璃纤维等间距排列，选出一个代表性体积，取该单元长度为相邻玻璃纤维的垂向距离L，宽度为玻璃纤维直径D，如图22.7所示。为了建立管道外压理论模型，首先需要确定加强层的材料弹性摩尔常数。(www.xing528.com)

图22.7　加强层体积单元代表

五个有效模量可以表示材料的本构关系。对于EL、μL2等较为成熟的弹性常数计算公式，Halpin-Tsai模型表示如下：

式中　EL、μL2——局部坐标系下沿玻璃纤维缠绕方向的弹性模量和泊松比；

VPE——PE所占的体积分数。

对垂直于玻璃纤维缠绕方向的弹性常数（E2、μ2L、GL2）计算公式，Halpin-Tsai模型给出如下公式：

式中　M——E2、μ2L、GL2中的任何一个；

Mfg、Mm——玻璃纤维和基体HDPE相对应的量；

ξ——经验系数，是对玻璃纤维增强作用的度量，可以从0变化到∞，其大小取决于玻璃纤维的几何尺寸、排列方式和加载方式，对圆截面玻璃纤维，方形排列时，弹性模量、泊松比的经验系数ξE、ξμ为2，剪切模量的经验系数ξG为1。