风轮转速和气动转矩关系特性曲线及多输入控制

6.3.1.1 理论最优控制

由于风的不稳定性和易受扰动的特性，因此及时准确地测量风速的方向和整个风轮的平均风速并不简单。下面介绍的控制方法是在已知风力机特征参数的情况下不通过测量风速来实现控制风力发电机。

整理式（2-5），用式（2-5）中描述的叶尖转速比λ与转矩系数和功率系数的关系，风轮的空气动力转矩变为风轮转速的函数如下：

回顾图2-6，当叶尖转速比为设计值λ_A时，风力机的功率系数为最大值c_p，max。假如风力机一直保持叶尖转速比λ_A，那么式（6-53）的系数部分就是一个常数，起动转矩也仅仅取决于风轮转速的平方。如下式所示，系数部分被写为因子K：

式（6-54）可以作为起动转矩的设定值控制策略。当风速在切入风速与额定风速之间时，需要风力机以最大效率转化风能，因此此时可以完全套用式（6-53）及式（6-54）的控制策略。

6.3.1.2 最大功率追踪法

另外一种广为接受的风力发电机最优化控制方法称为最大功率追踪（Maxi-mum power point tracking，MPP追踪）法。下面用光伏发电系统中的MPP追踪法来做类比，说明在风力发电系统中这个方法如何应用。图6-11左侧的曲线是光伏电池的发电特性曲线：图中标明了电流I相对于电压U的关系，以光辐射能E为参数。图中的P_max曲线标注出了最大功率曲线。图6-11右侧是风轮机的气动转矩T与风轮转速Ω的关系特性曲线，以风速v为参数。图中也标注出了最大功率曲线P_max。通过对比图6-11的左右两部分，可以看到一些共同点，当然风力机的大转动惯量造成远比光伏发电系统长的时间常数。

类似于光伏发电系统中的MPP追踪法^[Qua07]，参考文献[Schi02]提出了适合于风力发电机的最大功率点搜索算法：每隔一定时间检查风轮机的功率P、转速Ω，并且根据监测到的状态来改变风轮机的设计工况值。其增量方法思路如下：

1）如果ΔΩ≥0而且ΔP>0，那么下个周期增加转速；

2）如果ΔΩ≥0而且ΔP>0，那么下个周期降低转速；(www.xing528.com)

3）如果ΔΩ<0而且ΔP<0，那么下个周期增加转速；

4）如果ΔΩ<0而且ΔP>0，那么下个周期降低转速。

其中ΔΩ是监测到的转速变化值，ΔP是监测到的功率变化值。

转速设定值Ω还用于面向风电场的有功功率控制。在使用该方法时，并没有使用风速变量，因此对于这种控制策略，风速信息不是必需的。

其他参考文献中介绍的爬山算法（Hill Climbing Searching，HCS）其实也是这种MPP追踪法的变种。例如参考文献[Wan04]使用人工智能控制器在线训练估计。

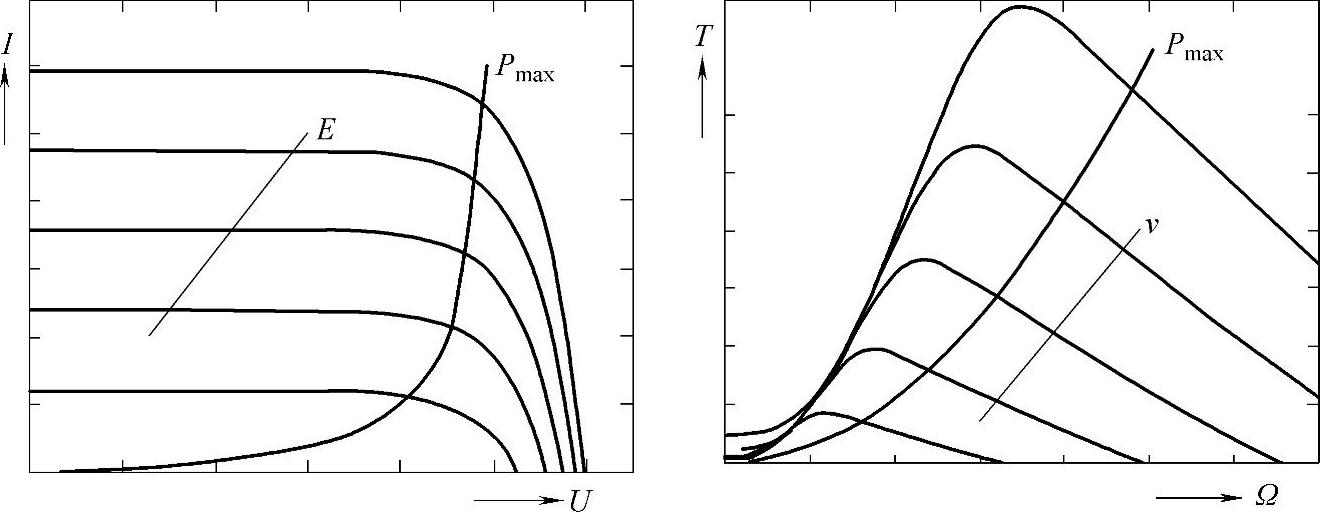
图6-11 光伏与风能系统对比

6.3.1.3 多输入控制

大型复杂系统往往有许多控制目标函数。例如大型的并网风力发电机服从运营管理系统的调度，需要调节有功功率P和转速n；使用逆变器的发电机还需要调节逆变器的无功功率Q；至于单个风力机内部控制变量如桨距角β等也需要控制器来调节。

现代控制器一般都采用闭环控制，控制器内部含有多个控制环路。一旦控制系统可以解耦，不同逻辑层次的环路可以级联。风力发电机的控制环路大多数都是可以解耦并且级联的，采用PI控制器。