抗弯刚度对受限压溃的影响比较

依上所述，对于φK=0和φK=+∞的情况，可以直接与已有理论公式进行比照，来对该模型在弹性受限条件下的有效性进行验证。需要注意的是，由于有限元的外压施加在内层的外表面，而理论是以中心线位置为计算标准的，因此可以简单使用平衡方程将理论结果转换到外层：

式中　Pc-out——作用在层外侧压力；

Pc-mid——作用在层中心线处压力。

计算结果总结见表11.2。

表11.2　平面应变模型理论与有限元结果比较

表中的误差表示有限元和理论计算结果的差异，可看出平面模型的屈曲压力与Timoshenko的理论计算结果非常接近，而刚性受限屈曲压力与Glock理论存在一定误差，初步判断是受到径厚比的影响，因此可以推测刚度比处于0和+∞之间的模型在很大程度上也是适用的。由Timoshenko计算结果和有限元结果之比可以看出，使用顶部加压的方式引入缺陷也可作为经典屈曲分析的方法，但需要说明的是，该方法不会发生分枝型屈曲，且第一次到达拐点后进入了一段平台阶段，因此该有限元结果是根据拐点估读出来的，这也和Vasilikis［4］的结论相一致。(www.xing528.com)

图11.4选出11个有代表性的抗弯刚度比φK绘出内层A点向下的位移与所施加压力的平衡路径曲线，所涉及抗弯刚度比列于图表右侧，将向下的位移设为正值，考虑到可能出现的对顶点自接触，将内层半径值70 mm作为水平坐标的最大值。各条曲线表示了不同约束条件下受限压溃从屈曲前到屈曲时再到初始屈曲后的全过程。

图11.4　不同φK下的位移-压力曲线

从图中可以看出，该问题的失稳属于非线性极值型失稳，图中所有的平衡路径均可以分为两大阶段，首先讨论第一阶段，在该阶段中，各平衡路径很快上升至极限外压，上升过程中随着φK变大，A点在极限屈曲处的位移逐渐向10 mm位置处靠近。

两个阶段的分界点是外压达到极限的时候，根据图11.4的结果，可将极限外压值随φK的变化趋势绘于图11.5，将数值方法得出的极限外压值进行标准化，即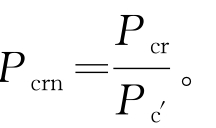观察结果发现，在φK=+∞时，Pcrn=7.60；而φK=595时，Pcrn=7.58。两者相差0.26%，极为接近，因此这里只给出0≤φK≤600范围的结果，刚度比大于600的情况可直接根据φK=595来进行估算。为表达清晰，0≤φK≤60的部分在图中单独列出。从图11.5可以观察到，在整体趋势中，屈曲压力随φK增大而增大，该曲线大致可分为三个阶段，当0≤φK≤3，Pcrn呈现较陡的线性上升形式，而超过φK=60，Pcrn趋于一近似的水平直线。这两段中间3≤φK≤60由一弧线相连，三段曲线可使用曲线拟合软件DataFit得出一组拟合计算公式，该组各个公式由修正的多重确定系数来进行拟合优度评估，该值越接近1，拟合优度越好。再按照各个区间端点的连续性，调整每个公式的系数，并使各点数值计算结果和拟合结果的差值小于5%，最终得到修正的拟合公式［式（11.4）～式（11.6）］，Pcrn-29代表径厚比为29的Pcrn。

图11.5　有限元和拟合公式的φK-Pcrn曲线