数值分析建模的关键要点

本章的有限元数值分析均基于5.5″非粘结柔性管来进行，该管基本的物理数据及简化的几何尺寸见表11.1，内层是以钢材为对象进行分析。

表11.1　双层非粘结柔性管有限元模型基本参数

注：*表示前者用于螺旋结构，后者用于环结构。

图11.2　双层模型受限内层的施压与初始扰动

如上所述，为保证运算精度，所有模型均采用隐式计算方法。使用弧长法分析时主要包括两个步骤，第一步为一般静态分析，主要是为了引入初始扰动，如图11.2所示，根据其心形失稳模态，在内层顶部θ=180°点A处施加垂直向下的微小位移。由于该分析的重点是模型的无缺陷屈曲，施加的位移值应该不影响屈曲压力值，同时又利于计算的收敛，通过参数分析，选用位移值δ0=0.1%Ri作为施加的初始竖向位移，同时可由此将初始椭圆度定义为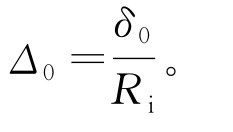(www.xing528.com)

第二步使用静态弧长法计算内层外表面施加径向外压时的响应，上一步的初始位移在第二步开始时即被移除，此时内层的相应部位上已经存在有初始扰动。在使用Riks算法时，设置的外压大小是任意的。

使用动态隐式算法主要为解决弧长法在某些情况下难以收敛的问题，与Riks分析过程相似，第一步需引入初始扰动，可在第一步静力分析结束后将变形后的几何构型重新导入建模，或不使用静力分析的方法，直接建立带有扰动的几何模型，以此完全消除静力分析产生的初始应力等影响，同时可以更准确地控制初始扰动大小。该方法应用于弧长法时较难收敛，因此仅当初始应力等对屈曲荷载影响很小时才可使用弧长法进行分析。

作为本研究的核心要点，受限约束主要是通过两层之间的接触产生的，且在压力加载过程中，接触状态也在不断发生变化，接触非线性对弧长法计算的收敛性提出了较大挑战，而对动态隐式的收敛性能影响相对要小。本章使用基准面的接触对来进行接触模拟，需判断并设置主从面，由于所选刚度比是通过外层材料弹性模量的变化决定的，为避免主面穿透从面，需根据内外层相对刚度的不同来手动调整主从面，在网格密度相近的情况下，将较硬材料设置为主面。接触面间的相互作用包含法向作用和切向作用，本章中法向作用采用硬接触，允许接触后再发生分离，一旦接触面间出现间隙，接触压力即变为0，正是这种接触压力的突然变化可能会带来收敛问题，而切向作用包括了界面间的滑动和摩擦，本章暂不考虑摩擦影响，为了模拟两层可能发生的任意幅度的相对切向运动，采用了有限滑动追踪方法。二阶单元在确定从面节点力时可能发生混淆，因此本章在包含接触的问题中均采用一阶单元来进行模拟，并通过加密厚度方向上的单元来防止沙漏能的产生。