关于外部约束体为弹性圆环的研究非常有限,Kyriakides[12]假定外环为可变形弹性体,对两个同心薄壁光滑接触的圆环在外环外部及两环之间的缺陷处受压的情况进行了研究,如果考虑非粘结柔性管的湿压溃情况,例如Lamber[13]所述,具体受力情况则有所不同,压力值P只沿内环的环向均匀分布,内外环之间的接触力与压力P的关系并不能确定,同时使用Kyriakides[12]方法来解决外部约束体为弹性的情况,最终依然落脚在复杂的数值求解方法上。
图10.6 弹簧支撑下圆管的屈曲模型
如上节所述,Malta[14]所研究的湿压溃内层失稳模式包含了椭圆、心形和过渡形,现研究受弹性限制内层的压溃模式趋于椭圆化失稳的情况,此时外层的约束只集中在两侧的端点上,如图10.6所示,可以使用弹簧侧边支撑来模拟该约束,弹簧的刚度取决于外层的抗弯刚度。因此可将这个问题简化为两端有弹簧支撑的内层圆筒在静水压下的屈曲分析,分析过程中采用了势能驻值原理。
将其视为薄壁圆筒,则所有变量只与极坐标系下的θ有关,如图10.6所示。令v和w分别表示圆筒中截面的环向和径向位移,这两个变量的表达式可以假设为
为了接下来的分析,首先推导出这些位移分量的变分如下:
同样根据非线性环理论,采用式(10.7)及式(10.8)来描述环向应变εθθ,内层的弹性势能可参考式(10.9)及式(10.10)。根据势能驻值原理:
而
其中,
求解式(10.65),可以得到屈曲压力为(https://www.xing528.com)
其中,
以式(10.1)为基础,Timoshenko求出在圆环对径压力作用下的圆环抗弯刚度,该方法也是试验确定圆环截面刚度的方法,求解可得到
式中 F——对径压力;
δ——该压力下径向收缩位移。
而从式(10.66)可知,在外压下,环截面抗弯刚度对其屈曲压力有直接影响。受此启发,考虑采用管道整体横截面的抗弯刚度作为约束标准,利用式(10.67),对于自锁层可采用式(10.15)来计算等效惯性矩,并可通过抗弯刚度相等求得等效厚度:
为同时考虑内外层作用,将外环与内环抗弯刚度比作约束等级,可由下式求得:
其中o表示外层,i表示内层,eq表示等效,应根据模型具体情况进行相应计算,若应用于无限长管的平面应变模型问题,需要将式中的E用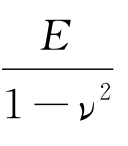 代替。
代替。
综上,式(10.66)又可表示为
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




