刚性限制下的圆管稳定理论

非粘结柔性管的湿压溃形式其实是圆管的受限压溃问题。目前的受限稳定理论大部分都是针对外部介质为刚性体或近似刚性体的情况，Cheney［6］所建立的屈曲模型要求外部刚性介质随内环向内移动，而Glock［7］假定刚性体不随着圆环向内移动，更符合刚性体特点。结合Omara［8］的补充解释，本节叙述了Glock［7］关于嵌于刚性体中的无缺陷圆环在均匀水压力下的稳定理论。为简化问题，首先进行如下假定：变形体中间直径对称；变形分离的部分为-φ≤θ≤φ；内环为均质各向同性线弹性材料；刚性体和圆环之间没有摩擦。和前文相同，此处模型中也是结合非线性变形理论应用能量原理进行求解。其推导过程如下：

如图10.3所示，w为径向位移，v为环向位移，根据Soifer［9］、El-Bayoumy［10］等人的研究，对平面应力问题的薄壁圆环有如下假定：

图10.3　圆环极坐标系下位移分量示意图［8］

与经典屈曲相同，采用非线性环理论，其环向应变的一般表达式为

其中同样只考虑中心线环向对位移的影响，以径向向外和切向顺时针为正：

式中　——圆环中轴线位移。

可假定式（10.28）可化为

将式（10.27）、式（10.29）代入式（10.26），其环向应变可表示为与式（10.7）相同的形式：

其中，

基于以上假设，薄壁圆环的应变能可以化简为

式中　V——圆环体积。

假设胡克定律适用，上式可改写为

式中　A——圆环截面面积。

Glock屈曲模型中将内环分为屈曲部分Ⅰ和非屈曲部分Ⅱ，如图10.4所示。将式（10.30）代入式（10.34），通过简化可得屈曲部分Ⅰ和非屈曲部分Ⅱ的应变能分别为

图10.4　Glock屈曲理论模型及受力分析图

其中，

由于非屈曲部分Ⅱ贴紧外部介质，则系统总势能为

其中第一项代表屈曲部分环中心线曲率改变产生的内能，第二项为环中心线轴向应变产生的内能。将式（10.37）、式（10.38）代入式（10.39），得到

为了简化总势能表达式，使其只含有一个未知位移量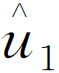，Glock假定：

为弥补采用此假定而去掉的U2，Glock将由环向应变产生的应变能密度进行平均，假定沿整个环的环向力为常数，将其在屈曲部分进行积分再沿整个环进行平均得到(www.xing528.com)

屈曲部分的径向变形可以假定为

将上两式代入式（10.40），经过积分求解可得

同样采用势能驻值原理，对上式变分，可得

式（10.46）可化简，分别求得

两式联合可求解出

将其代入式（10.42），可得

求解该一元二次方程，可得

而将式（10.49）代入式（10.47），可得

将式（10.51）和式（10.52）联合，并令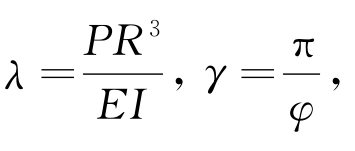可得：

可通过求解求出屈曲压力Pcr，可得

解得符合条件的根为

将其代回式（10.53），最终得到

图10.5　三塑性铰破坏模型

上述主要是针对受限弹性环的屈曲压力求解，Vasilikis［11］基于内环为弹塑性材料数值求解的结果，发展了塑性铰理论的求解方法，以此来描述屈曲后的压溃行为。假定内衬管为刚塑性材料，不可伸长，变形只发生在塑性铰处，其中包含两个移动的塑性铰和一个静止的塑性铰，如图10.5所示。对于单位长度圆筒，忽略轴向压缩对塑性功的影响，其全截面塑性弯矩为

内部塑性功的速率为全截面塑性弯矩乘以三个塑性铰∑ω的相对旋转角速率之和：

忽略了移动塑性铰的平移功。而单位长度外功速率为

利用内外塑性功速率相同，得到

该公式描述了出现三个塑性铰的屈曲规律，但在应用时δ不能直接确定，影响具体的压溃值计算。