风速的统计分布分析

一个地区的风速、风向时间、空间的变化规律及特性称为风情，每个地区的风情都受到许多因素的影响，如大的区域性气候影响，小的局部地区地形影响，并且风力的变化还明显受到季节影响，甚至还有短期的随机变化等。因此在风力发电场的选址工作中，对风情的考察和预测是至关重要的。一般风情数据都是通过测风塔来观测和记录的，测风塔能够监测某一固定高度的风情数据。但是即便同一地区的记录数据在不同时间也会有一定的波动。

地表的高低起伏无疑会对风情产生影响，在风力机所在的高度范围内，风速由低到高增加，国际上常用一个指数函数来表示层流风速v和高度z之间的关系，即

式中，v₁是在参考高度z₁的水平层流风速；z₀是地面粗糙特征值，它根据风电场周围的地形不同而取不同值。例如，如果周围是开阔平缓的农田，z₀取值0.03m，如果周围是稀疏的树林和灌木丛，z₀取值0.1m，如果周围分布着茂密的森林，z₀取值0.5～1.6m。本书的2.4.4节中，在评估风力发电机的参考捕获能量时也使用了式（2-9）。

一旦风速v（t）有了一个明确的以高度表示的函数表达式，那么风力发电机的捕获能量功率和总捕获能量都可以通过描述统计学方法来计算。

首先把所考虑的风速范围划分为k个等级，每个等级涵盖的风速范围都是Δv，第i（i=1，2，3，…，k）个等级的平均风速为v_i。每隔一定的时间测量一次风速，并且把测量的结果归入这k个等级的图谱之中。把每次测量的风速v_i都当作是时间段t_i之内的平均风速，这样就可以计算v_i风速的相对出现频率为

式中

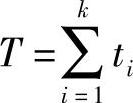
用直方图表示不同风速等级频度分布h_i（v_i）图2-8是这种统计方式的一个例子，在这个例子当中，风速分级范围Δv=1m/s。(www.xing528.com)

通过长期的观测数据积累，现在业界普遍认为风速等级频度图符合韦伯分布规律。欧洲内陆地区的风速分布特征，更是属于一种特殊的韦伯分布，即瑞利分布（k=2）。

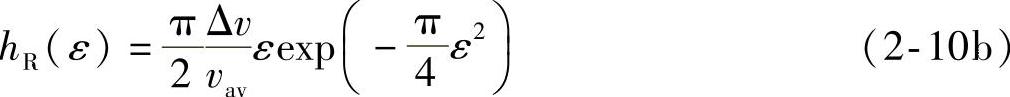
式中

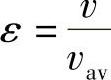
图2-8b展示了随着参数k的变化，风速韦伯分布的图形，其中当k=2时，韦伯分布又被称为瑞利分布，这种分布被业界广泛接受。

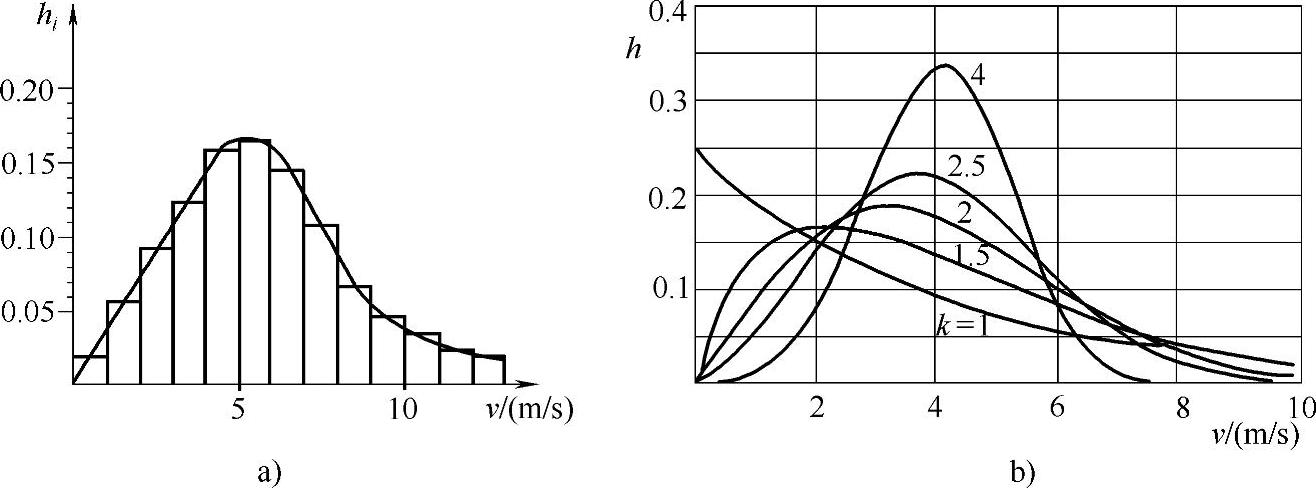
图2-8 风速分布示意图

a）直方图 b）韦伯函数近似表示（瑞利函数，其中k=2）