根据翼形理论对一片叶片升力和阻力的计算,可以得到风轮的主要参数。假设一个宽为b,弦长为t的翼形单元,有速度为v1的气流通过,如图2-4所示。攻角α为风向和翼形弦线的夹角,得到升力FA(垂直于气流方向)和阻力FW(平行于气流方向)分别为

注意,这两个分力分别垂直、平行于气流方向。系数cA和cW表示了给定叶片轮廓的特征,取决于攻角α。将图2-4中的范例应用于实际的非对称轮廓[Schm56],对于小的α值(0≤α≤10°),可以得到近似的比例关系为cA=(5.1~5.8)α,而cW在此区间内相对较小。称比值ε=cA/cW为升阻比。
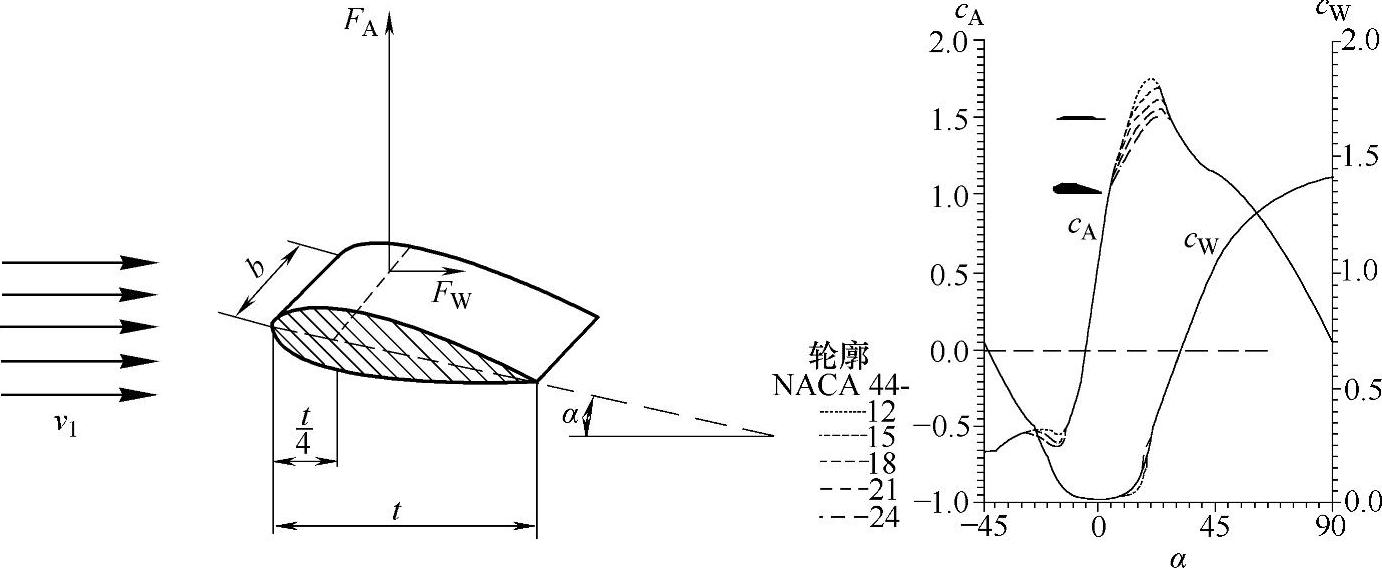
图2-4 特定翼剖面下升力系数cA(α)和阻力系数cW(α)随攻角变化曲线
当风轮以角速度Ω旋转时,叶片上距离旋转风轮轴线r处的圆周切向速度为u(r)=Ωr。根据Betz理论,风轮平面处的轴向风速为v2,其值为上风向风速v1的2/3。切向速度和轴向速度的矢量合成为该点处的相对风速c(r),c(r)与风轮平面之间成α角,如图2-5所示。升力和阻力的微元变量dFA和dFW全都作用于该点附近的叶片面积(tdr)内,则力分解得到的切向力dFt和轴向力dFa分别为
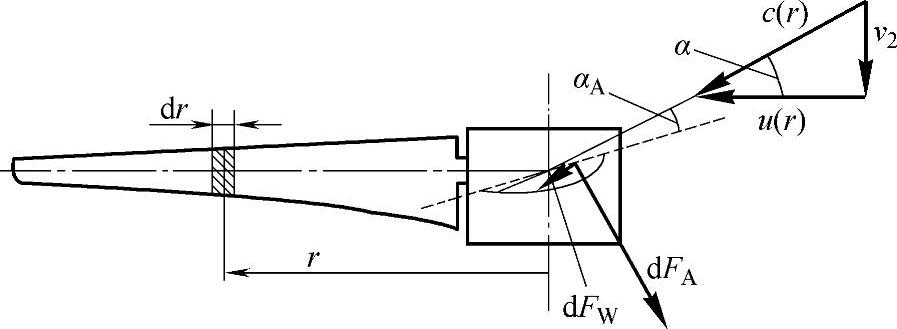
图2-5 叶片作用风速和作用力示意图

在给定的叶片轮廓上进行积分,可通过切向力得到转矩,轴向力合力得到轴向作用在风轮上的阻力。
在叶尖处,r=R,叶尖切向速度为u(R)=ΩR。叶尖的相对风速为(https://www.xing528.com)
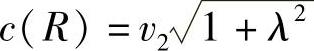
对于一个给定叶片角的风轮,图2-6[Gas07]给出了其cP(λ)和cT(λ)曲线,从而可知该风轮的设计最优叶尖转速比为λA=6.5。

图2-6 三叶片风轮功率系数cP(λ)和转矩系数cT(λ)曲线
功率系数cP(λ)和转矩系数cT(λ)是风轮基本特征参数(见2.2节、2.3节)。另外为计算风轮的轴向阻力,定义了轴向阻力系数cS(见图2-7)。对于刚性叶片,低λ时cS值也很小,并且在无负载速度(高λ)时,测量的曲线类似一个受轴向风载圆盘的情况。
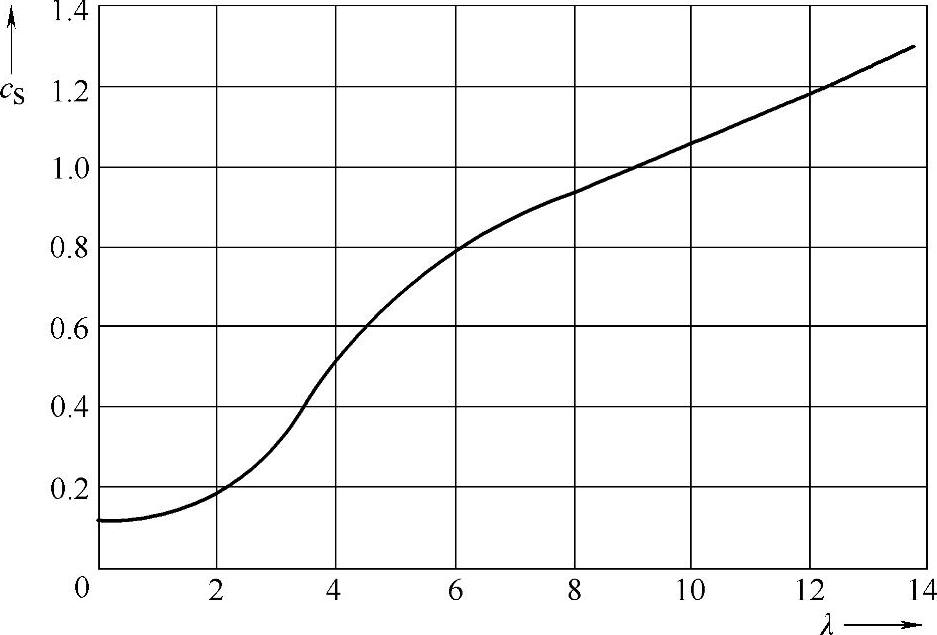
图2-7 阻力系数cS(λ)曲线
转矩T、功率P和轴向阻力S都可以用参考力FB来表示。FB正比于风速的平方和风轮扫掠面积,即
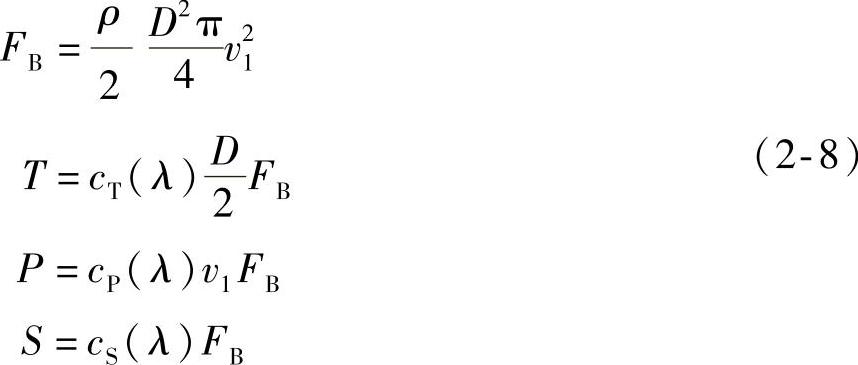
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




