吸附热力学概念及其在纤维上染过程中的应用

描述染液中的染料是否容易上染到纤维上去的热力学概念主要有化学位、亲和力和直接性。

染料的聚集是拆散染料与水分子之间的作用力形成染料与染料分子间作用力而相互聚集的过程，染料对纤维的上染是拆散染料与水分子间作用力形成染料与纤维间作用力而上染纤维的过程。染料在染液中的聚集以及染料从染液中上染到纤维的过程可以用体积自由焓的变化来考虑。而从染色热力学理论出发，这一过程可以用化学位来说明。

染料在染液中的自由焓Gs随着染液中染料浓度的提高而增加。染料在染液中的化学位（μs）是在温度、压力不变的情况下，在染液中加入无限小的该染料（i组分）∂ni摩尔，溶液中其他组分的含量不变，加入每摩尔这种染料所引起的体积自由焓的增量，叫染料在染液中的化学位，也叫该染料（i组分）的偏摩尔自由焓，表示如下：

在上述条件下，化学位表示的是溶液的自由焓随染料摩尔数的增加而增大的变化率。曲线在某一点的斜率越大，染料在染液中的化学位越高，则染料从染液中上染到纤维上的能力越大。染料在纤维上的化学位也是如此。同理，染料在纤维上的化学位可以表示为：

染料在纤维上的化学位越高，表示染料从纤维上解吸下来的可能性越大。众所周知，在上染的过程中吸附和解吸是同时进行的。在上染的初始阶段，染料在染液中的化学位大于染料在纤维上的化学位，吸附的速率大于解吸的速率。也就是说单位时间内从染液中上到纤维上去的染料量大于从纤维上解吸下来的染料量，即μs＞μf。随着上染过程的推进，染液中的染料量逐渐减少，纤维上的染料量逐渐增加，吸附的速率逐渐降低，解吸的速率逐渐增加。当达到平衡时，染液中的染料化学位和纤维上染料的化学位相等。即：

μs＝μf

染料在染液中的化学位是它活度αs的函数。设标准状态下的活度αs＝1的化学位为μs°，则：

μs＝μs°＋RTlnαs

式中：μs——染料在染液中的化学位；

μs°——染料在染液中标准状态下的化学位；

αs——染料在染液中的活度。同理，染料在纤维上的化学位是它在纤维上活度的函数。则：

μf＝μf°＋RTlnαf

式中：μf——染料在纤维上的化学位；

μf°——染料在纤维上标准状态下的化学位；

αf——染料在纤维上的活度。

当达到平衡时，则有：

μs°＋RTlnαs＝μf°＋RTlnαf

移项得：

-Δμ°称为染料对纤维的染色标准亲和力，或染色亲和力，简称亲和力。它是染料在染液中的标准化学位和纤维上的染料标准化学位之差，它是温度的函数。某一温度下的染色亲和力，可以从该温度下上染达到平衡时纤维上的染料活度和染液中的染料活度的关系来求。它标志着该温度下上染达到平衡时纤维上的染料活度和染液中染料活度的关系，是衡量染料对纤维上染的一个速率指标。

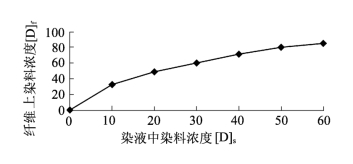
因此，要求染料对纤维的染色亲和力，必须求出某一温度下上染达到平衡时纤维上的染料活度和染液中的染料活度，而染料在染液中的活度根据染料在染液中的状态是可以求得的。染料在纤维上的状态是很复杂的，为了求出染料在纤维上的活度，就必须对染料在纤维上的状态做出假设，而这些假设的依据就是吸附等温线。吸附等温线是在恒定温度下，上染达到平衡时，纤维上的染料浓度与染液中染料浓度的关系曲线。染料对纤维上染的吸附等温线有三种类型，即能斯特吸附等温线、朗缪尔吸附等温线和弗莱因德利胥吸附等温线。在含有食盐电解质的水溶液中，用直接染料、活性染料以及还原染料等对亚麻纤维的上染，其吸附等温线属于弗莱因德利胥吸附等温线。其形状如图7-2所示。

(www.xing528.com)

图7-2　染料的亚麻纤维上得吸附等温线

从图7-2中可以看出，在恒温的条件下该吸附等温线有以下特点：

①纤维上上染的染料量［D］f随着染液中染料量［D］s的增加而增加；

②［D］f／［D］s的比值随着染液中染料量的提高而逐渐变小，并不是一个常数；

③染料在亚麻纤维上的上染没有染色饱和值，属于多分子层的吸附。

该曲线的经验方程式为：

式中：K——常数；

n——大于0而小于1的整数。

该式也可以写成：

ln［D］f＝lnK＋nln［D］s

通过弗莱因德利胥吸附等温线对上述染料在亚麻纤维上状态所作出的假设，可以求出上述染料对亚麻纤维染色的亲和力。上述染料在含有食盐电解质的溶液中对亚麻纤维的上染过程是染料在亚麻纤维表面发生吸附，但分子的热运动驱使染料分子在染液中在纤维附近做扩散层的分布。这样染料在亚麻纤维的界面附近形成一个浓度逐渐降低到和染液本体浓度基本一致的扩散吸附层，如图7-3所示。该曲线代表浓度随距离而变化的情况，达到A—A界面时浓度已基本与染液的本体浓度相当。设每千克干纤维含有吸附层的容积为V升，染料的大分子NazD会离解成Na＋和Dz-，分布在扩散边界层中，活度系数为1，则纤维上染料的活度为：

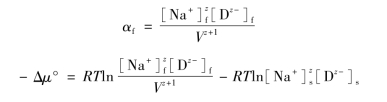
作图得一个直线，如图7-4所示。上式也可以写成：

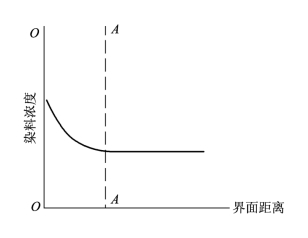
图7-3　染料在界面的扩散吸附层

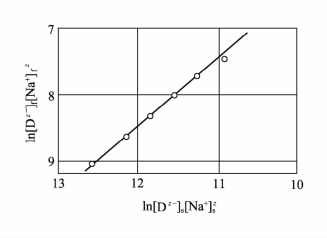
图7-4　直接天蓝FF对纤维素纤维上染的的关系曲线

如果染液中加入一定量的食盐，使［Na＋］s恒定，纤维上除了染料的阴离子以外，其他阴离子可以忽略不计，那么Na＋≈z［Dz-］f，对某一染料以不同浓度在等温条件下对指定的纤维上染来说，V和-Δμ°都是常数。在αf＝（［Na＋］f／V）z这种情况下，上式可以变成：

这是一个典型的弗莱因德利胥方程式。

从以上可知，染色亲和力是一个定量的热力学概念，而染料的直接性却没有确切的热力学概念。它只是笼统地说明染料对于纤维织物的上染能力。一般认为，上染百分率越高，染料的直接性越强；反之，上染百分率越低，染料的直接性越差。而上染百分率的提高又与染料的原始投入量等因素有很大关系，例如，染料的原始投入量越大或染色时的浴比越大，会降低染料的上染百分率。而染色亲和力却只与染料和纤维的性质有关，有确切的热力学概念，可以定量地说明在一定温度下染料对纤维的上染能力。