GB150与JB/T4731：两种压力容器标准的比较

原GB 150（1989）列有卧式容器的内容，GB 150（1998）则予取消，另列于JB/T4731（2005）《钢制卧式容器》，且与之配套的为JB/T 4712.1（2007）《容器支座 第1部分：鞍式支座》。

1.结构分析

支承于对称布置双鞍座上的卧式容器犹如一受均布载荷的外伸简支梁，其横向剪力和轴向弯矩在各处的变化关系如图7-1所示，在跨距中间和支座处截面可能引起较大的弯矩，因此，除必须对由压力引起的周向和轴向支座反力计算外，还必须对此两处可能的危险截面上因卧置而引起的各附加应力进行计算并校核。

为使支座处截面和跨距中间处截面圆筒的弯矩接近，使圆筒各截面的应力分布更为合理，根据受均布载荷时外伸简支梁的分析，外伸长度A和圆筒总长L（都以封头切线处起量）的关系当A=0.207L时，可得该两截面处的弯矩相等；此外，由于封头在承受轴向弯时其抗弯刚度大于圆筒，故往往利用封头对圆筒抗弯和抗剪的加强作用，即尽量使外伸段A值减小。为此，JB/T 4731规定，应尽量使A小于或等于0.5R_a；当无法满足时，A值不宜大于0.2L。

为适应自重（包括物料）或温度变化而引起容器的挠曲或轴向伸缩，当容器焊在鞍座上时，其中的一个鞍座应采用滑动支座或滚动结构，或将鞍座底板上的基础螺栓孔沿容器轴向开成长圆孔。

鞍座包角θ的大小不仅直接影响到鞍座处圆筒上的应力分布，而且也影响到容器-鞍座系统重心的高低。一般常用的鞍座包角θ值为120°、135°和150°三种，与之配套的JB/T 4712.1鞍式支座则列有120°和150°两种标准鞍座。

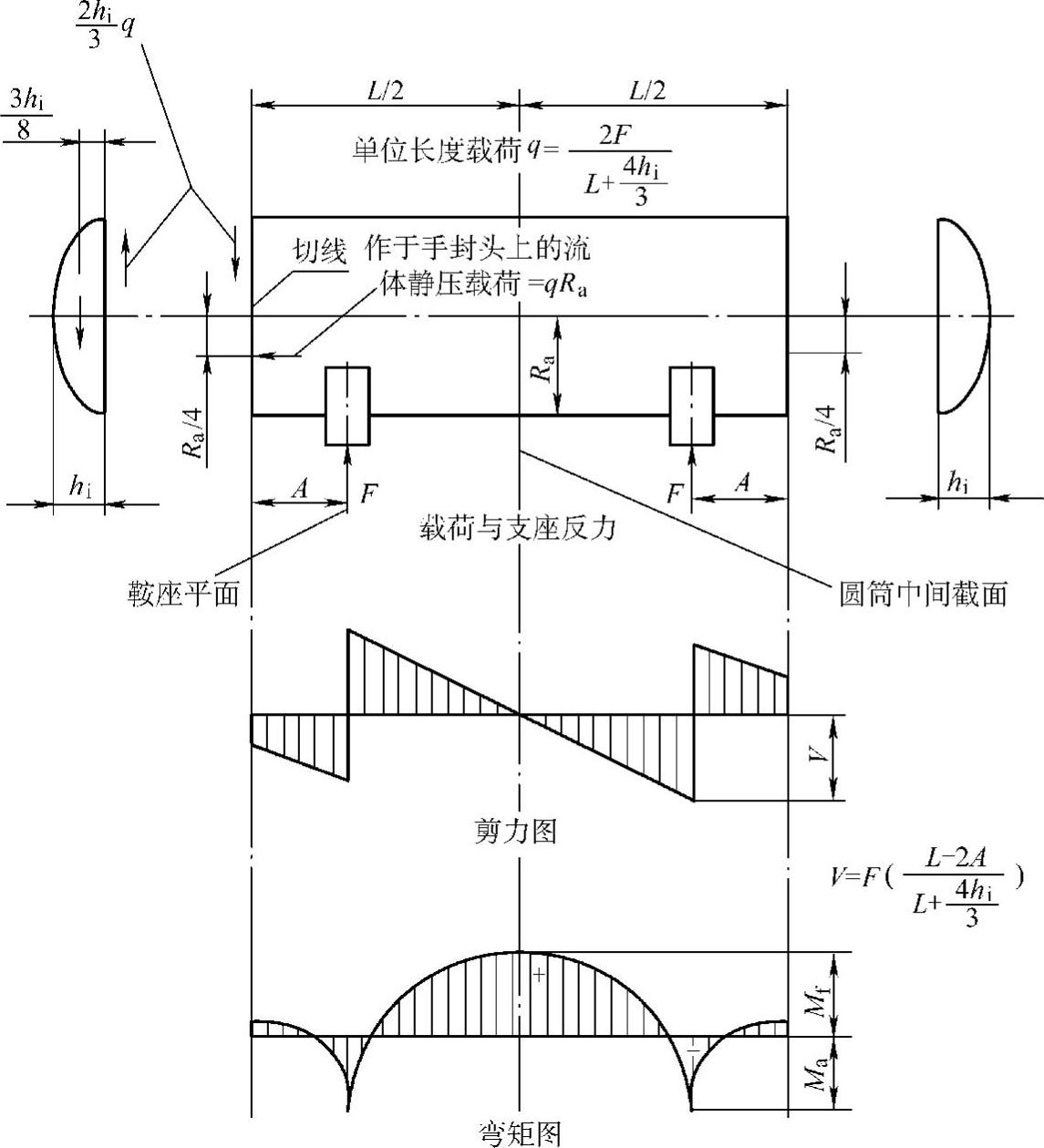
图7-1 双鞍座卧式容器的载荷分析（引自JB/T 4731图7-2）

2.载荷分析

（1）轴向弯矩分析 取容器总重（自重、物料或压力试验时充水）为mg，则每一支座反力为F=0.5mg。把卧式容器视为外伸简支梁，则其单位长度上所受的均布载荷q分别为：带凸形封头时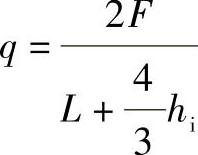，；带平封头时，。

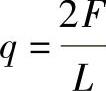两鞍座中间处截面上的轴向弯矩M₁可由材料力学的弯矩计算原理求得：

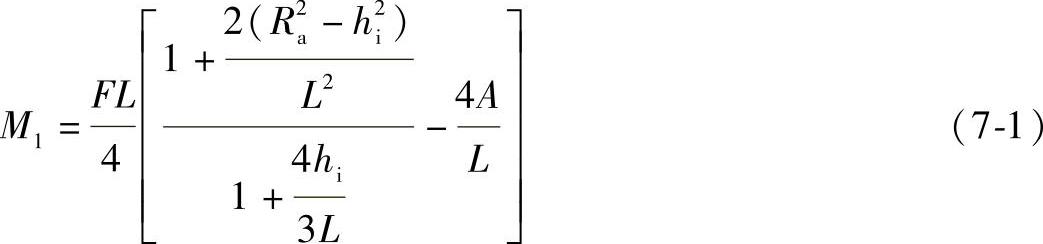
鞍座处截面上的轴向弯矩M₂为

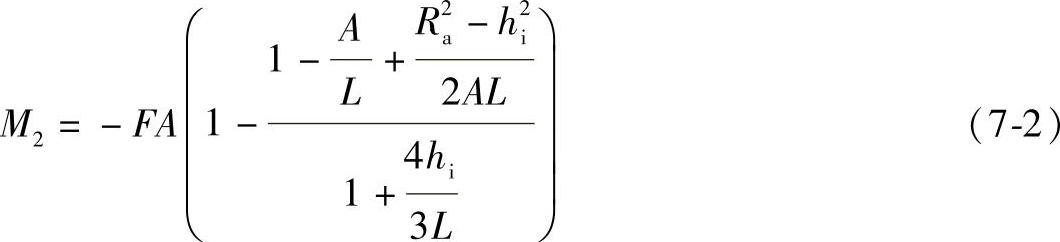
（2）横向剪力分析 两鞍座中间处截面上的横向剪力为0。鞍座处截面上的横向剪力应区分鞍座远离封头和鞍座靠近封头两种情况分别计算。

鞍座远离封头，即A＞0.5R_a时，应计及外伸圆筒和封头重量的影响，可得

鞍座靠近封头，即A≤0.5R_a时，可略去外伸圆筒和封头重量的影响，可得

V=F （7-4）

3.各处应力计算及校核条件

（1）圆筒上的轴向应力 圆筒上的轴向应力包括由压力引起的薄膜应力和由弯矩引起的弯曲应力两部分。

1）两鞍座中间处截面。弯矩M₁引起的弯曲应力最大值在圆筒上方点①处为压，圆筒下方点②处为拉，由整个圆筒承受，见图7-2。

2）鞍座处截面。如果在此截面上设有加强圈，或虽未设加强圈，但鞍座的布置满足A≤0.5R_a，即封头对鞍座截面处的圆筒能起加强作用，则可由整个圆筒承受弯矩M₂，此时弯曲应力最大值在圆筒上方点③处为拉，圆筒下方点④处为压，见图7-2。

如果在此截面上并无加强圈，且鞍座的布置导致A＞0.5R_a，即不能得到封头的加强时，则会导致圆筒的上半部分出现抗弯的无效区，即产生“扁塌”现象，见图7-3。此时仅圆筒的下半部分能承受弯矩M₂，其拉伸应力的最大值在该图有效承载面的上方点③处，显然，其应力值必较无“扁塌”现象时为大，规范引入系数K₁、K₂表示。

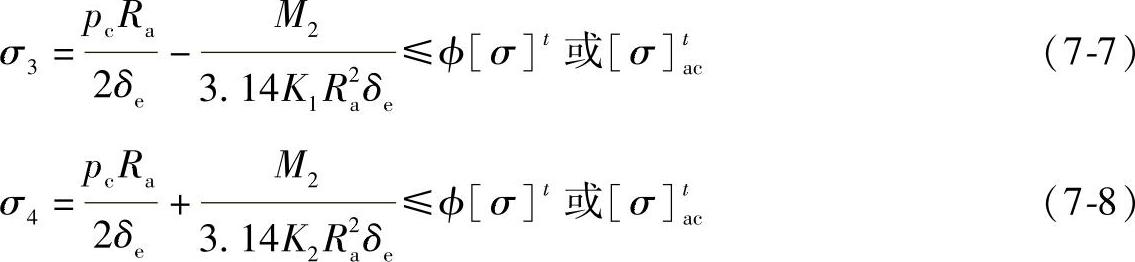
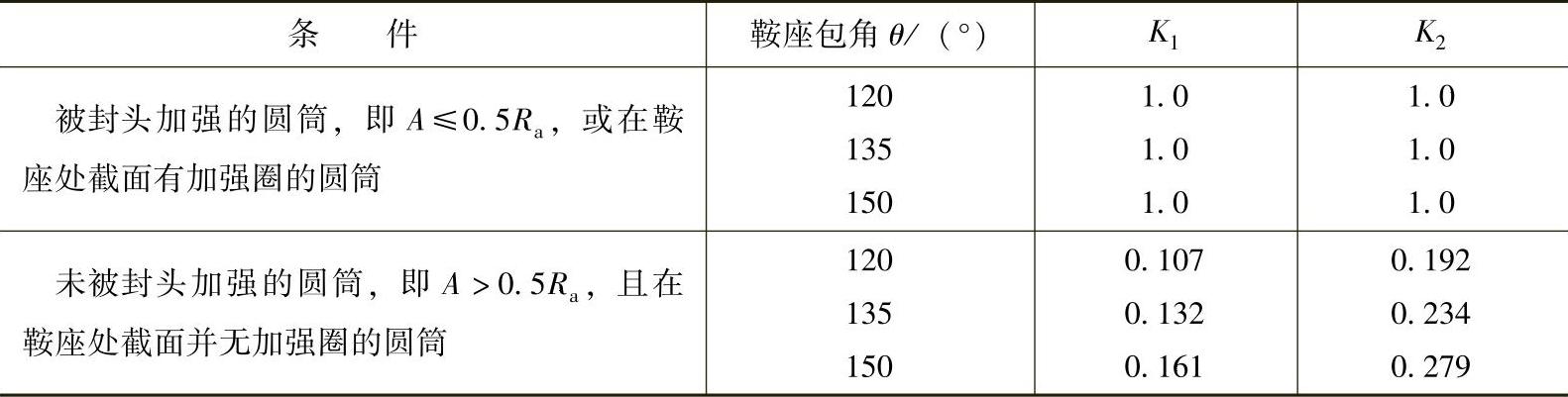
式（7-5）～式（7-8）中，ϕ为圆筒上的环向焊接接头系数；K₁、K₂为计及“扁塌”现象的系数，根据圆筒结构和鞍座包角，列于表7-1；其余各符号的含意可查标准JB/T 4731—2005，不再详述。

要注意的是，当容器内充满物料或水而内压尚未升起时，最高点①或最低点④的压缩应力为最危险工况，必须校核。

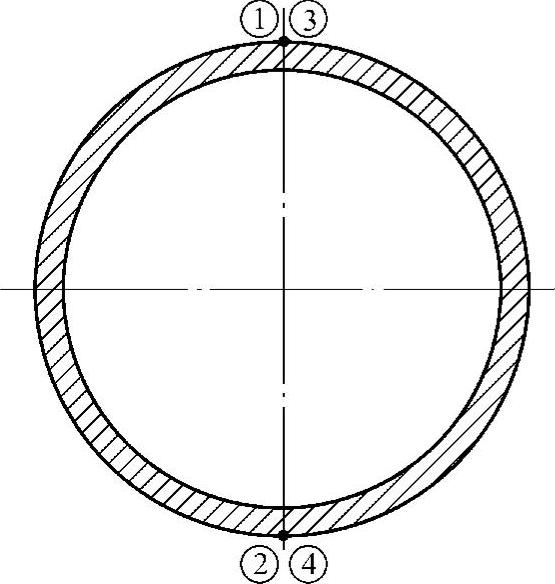
图7-2 由整个圆筒承受时圆筒上弯曲应力最大值的位置

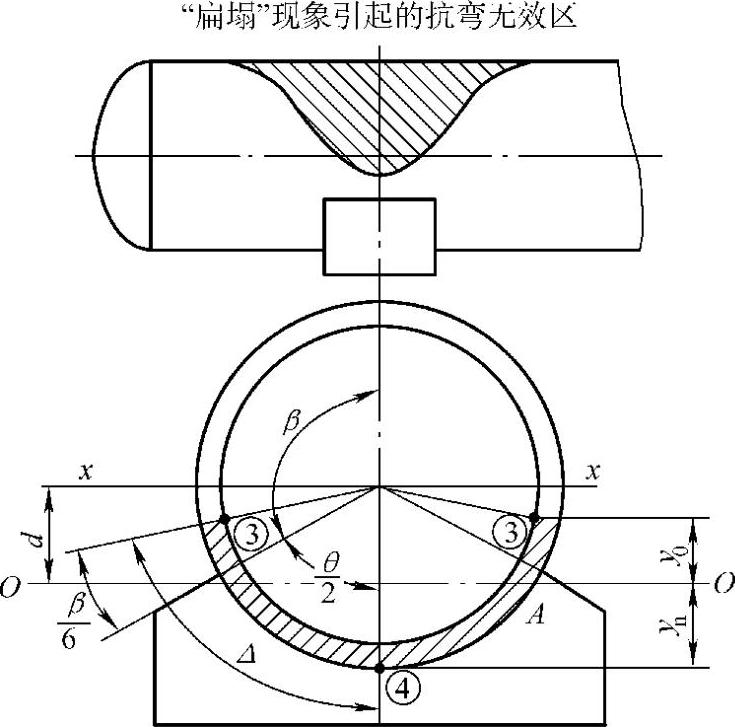
图7-3 “扁塌”现象及其最大应力位置

表7-1 系数K₁、K₂（引自JB/T 4731表7-1）

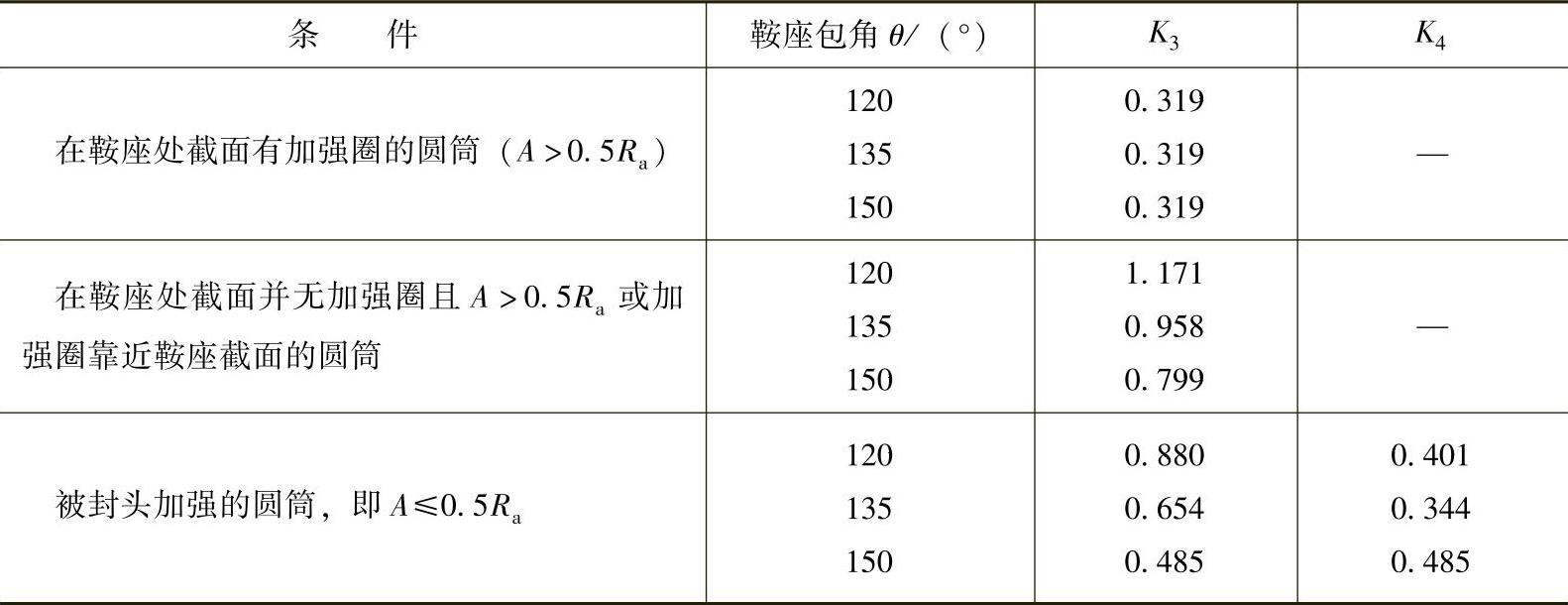
（2）圆筒或封头上的切向剪切应力 由横剪力V对圆筒或封头引起切向剪切应力，和承受弯矩M₂时视圆筒结构而可能引起“扁塌”现象相似，如鞍座截面上圆筒设置了加强圈，则由整个圆筒截面承受剪切应力，其最大值在A、B点处，见图7-4；如鞍座截面上圆筒并无加强圈，且鞍座的布置导致A＞0.5R_a，即不能得到封头的加强时，圆筒也会引起抗剪截面的无效区而使剪切应力增大，其最大值在C、D点处，见图7-5；或虽无加强圈，但鞍座的布置满足A≤0.5R_a，即封头对圆筒的抗剪能起加强作用时，则圆筒和封头的切向剪切应力分布如图7-6所示，其最大值也在C、D点处。规范都采用引入系数K₃、K₄表示，见表7-2。要说明的是，抗弯和抗剪无效区虽然都由同一原因引起，但其无效区的大小是不同的。

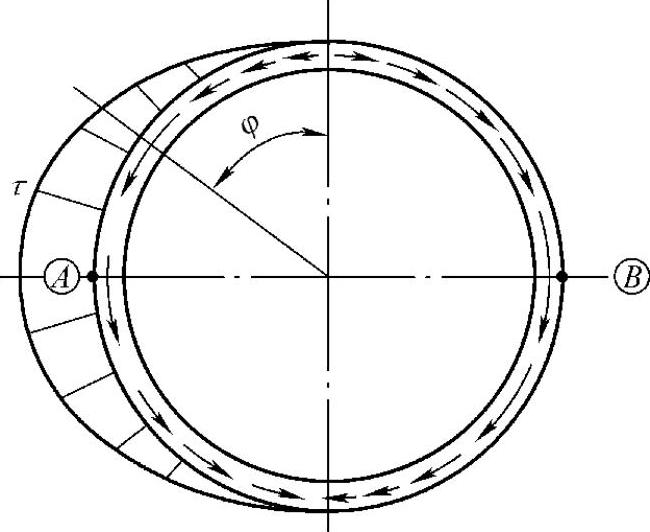
图7-4 圆筒由加强圈加强时的剪切应力分布

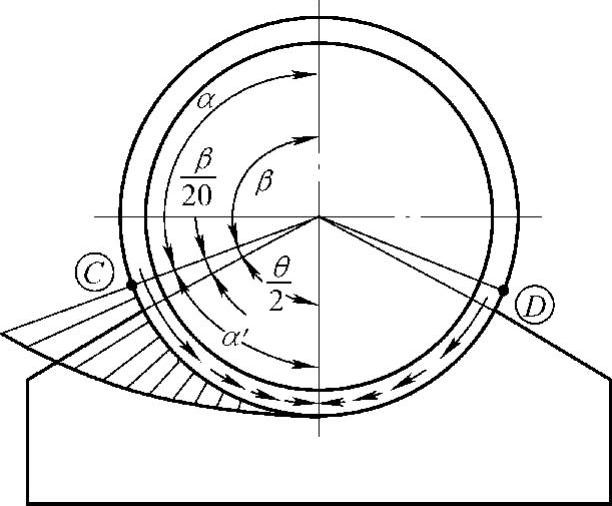
图7-5 圆筒未被加强时的剪切应力分布

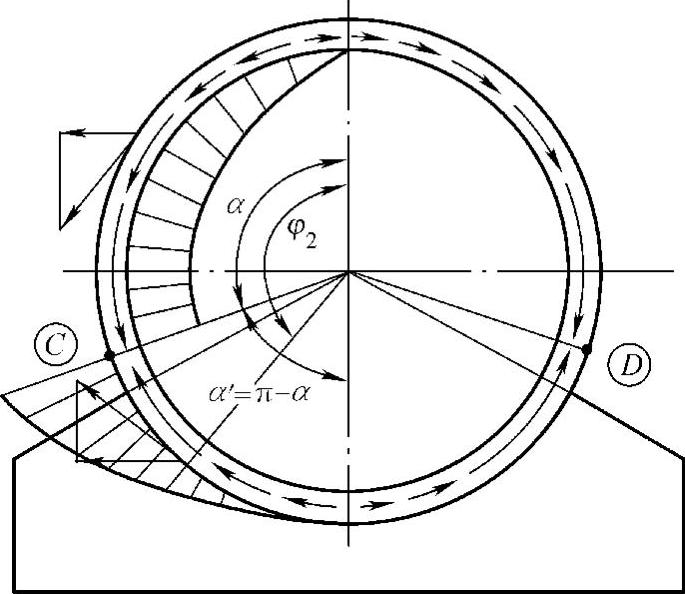
图7-6 圆筒被封头加强时的剪切应力分布

表7-2 系数K₃、K₄（引自JB/T 4731表7-2）

鞍座远离封头（即A＞0.5R_a）、圆筒在鞍座截面设有或并无加强圈时，圆筒上的切向剪切应力按下式计算和校核：

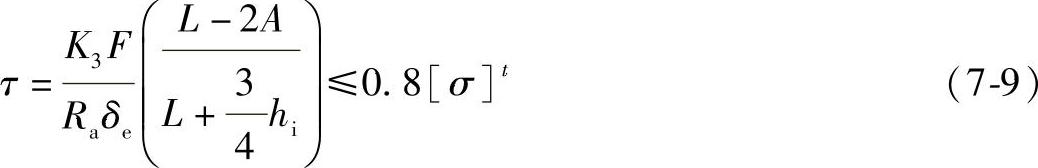
圆筒在鞍座截面并无加强圈，但鞍座靠近封头（即A≤0.5R_a时），圆筒或封头上的切向剪切应力按下式计算和校核：

圆筒上 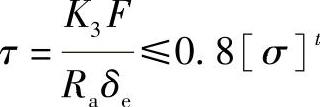（7-10）

封头上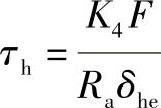

封头上切向剪切应力的校核条件为

τ_h≤1.25[σ]^t-σ_h （7-11）

式（7-11）中，当为椭圆形、碟形或半球形封头时，σ_h分别为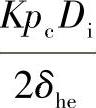、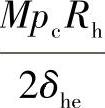或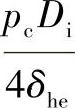，即分别由椭圆形、碟形或半球形封头的设计公式导得。

（3）在鞍座截面处圆筒上的周向应力 圆筒上的周向应力由周向弯曲应力和周向压缩应力两部分组成。

周向弯曲应力由圆筒上的切向剪切应力所导致的周向弯矩引起，由于切向剪切应力和圆筒上在鞍座截面处是否设置加强圈，鞍座的布置是否靠近封头（A＜0.5R_a），或在鞍座截面处并未设置加强圈（包括加强圈设置在靠近鞍座截面处，但不是在鞍座截面处）且A≥0.5R_a等情况有关，所以周向弯曲应力也和这些情况有关。

周向压缩应力由鞍座对筒体的支承反力以及圆筒上的切向剪切应力所导致的周向压缩力所引起，所以和鞍座包角θ、影响圆筒上切向剪切应力分布的因素（见上述）有关。

在计算周向弯曲应力时所用到的圆筒抗弯断面模量，据L.P.Zick的实测结果，认为和圆筒的L/R_a值有关，当L/R_a≥8时，圆筒计算宽度为4R_a，当L/R_a＜8时，圆筒计算宽度为L/2。

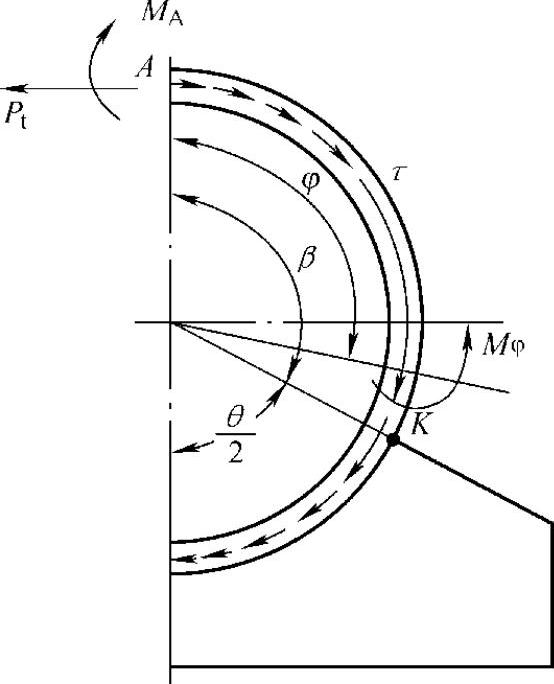
图7-7 鞍座截面处圆筒上设有加强圈时周向弯矩Mϕ的计算模型

圆筒上由切向剪切应力所引起周向弯矩Mϕ的计算模型（当鞍座截面处圆筒上设有加强圈时）见图7-7；由支座反力和圆筒上切向剪切应力所引起周向压缩力T的计算模型见图7-8；圆筒上周向弯矩Mϕ和周向压缩力T沿圆筒周向的分布示意见图7-9。

由图7-9可见，圆筒上的周向弯矩M_β在鞍座包角边缘处达最大，同时在此处还有一定值的周向压缩载荷T；而在圆筒底部，周向压缩载荷达最大，为T_max。为此，应对鞍座包角边缘处的周向组合应力（由周向弯曲应力和周向压缩薄膜应力组合而成）以及圆筒底部的周向最大压缩薄膜应力进行计算并校核。当然，在计算时应针对各种结构（如是否在鞍座截面处设置加强圈，鞍座离封头距离的大小等）区别对待。

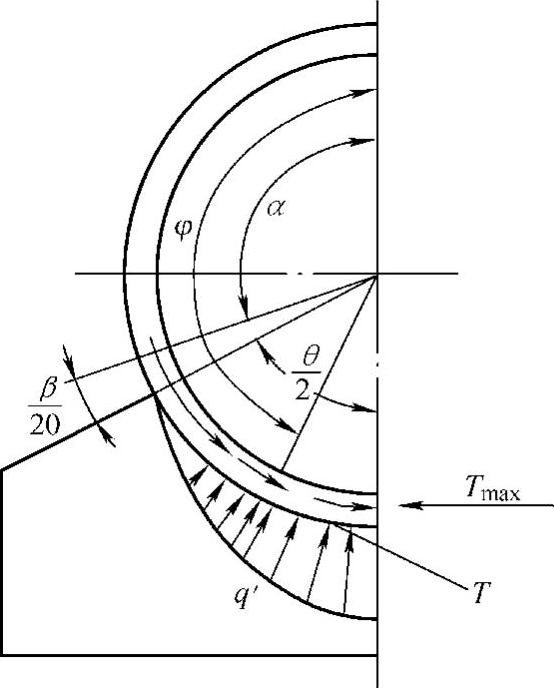
图7-8 由支座反力和切向剪切应力所引起周向压缩力T的计算模型

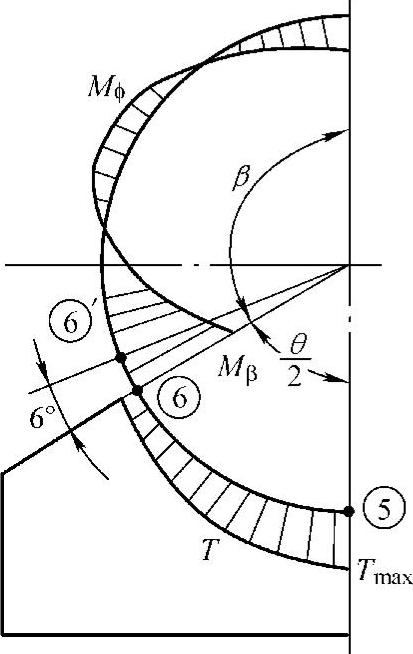
图7-9 周向弯矩Mϕ和周向压缩力T沿圆筒周向的分布示意

对在鞍座截面处设置加强圈的情况，放在最后讨论。

1）鞍座截面处及其附近并无加强圈的圆筒。此时仅考虑A≤0.5R_a或A＞0.5R_a两种情况，涉及在周向弯矩计算中所引起的区别，以应力公式中所用系数各有不同加以体现。(www.xing528.com)

在周向组合应力以及周向最大压缩薄膜应力的计算中，又要区分在鞍座上是否设置垫板：设置垫板时，可由圆筒壁和垫板一起承受载荷；不设垫板时，仅由圆筒壁单独承受载荷。

所设垫板的尺寸在同时满足以下三个条件时才能起到对圆筒的加强作用：①垫板厚度不小于0.6倍圆筒厚度；②垫板宽度不小于圆筒有效宽度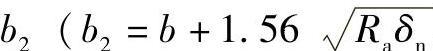，b为鞍座的轴向宽度）；③垫板包角应不小于θ+12°。如不满足其中任一条件，则即使设置了垫板也不能起到对圆筒的加强作用。

①无垫板或虽有垫板但垫板尺寸不足，致不能起加强作用时，在圆筒截面最低点处的周向压缩薄膜应力为

在鞍座边角处圆筒上的周向组合应力：

当L/R_a≥8时，

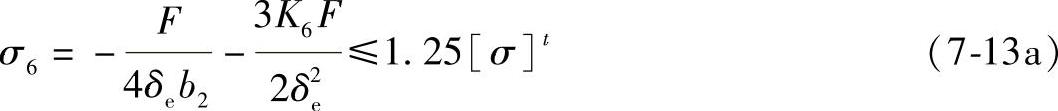
当L/R_a＜8时，

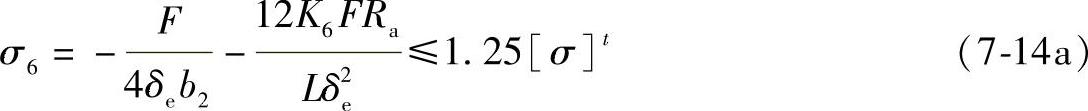
②有能起加强作用的垫板时，可由垫板和圆筒壁厚之和承受载荷。在圆筒截面最低点处的周向压缩薄膜应力为

在鞍座边角处圆筒上的周向组合应力：

当L/R_a≥8时，

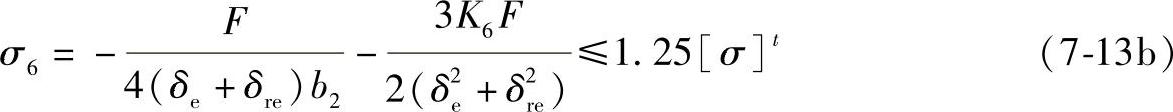
当L/R_a＜8时，

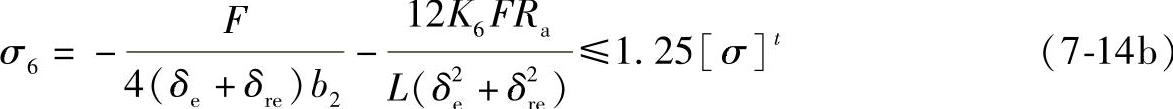
由图7-9可见，在离鞍座边角6°即垫板边缘处，虽然周向弯矩有所减小，但由于已无垫板，所以此处的周向应力系由圆筒壁单独承受，需要按以下公式另行计算和校核。

当L/R_a≥8时，

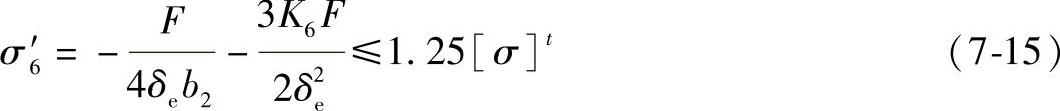
当L/R_a＜8时，

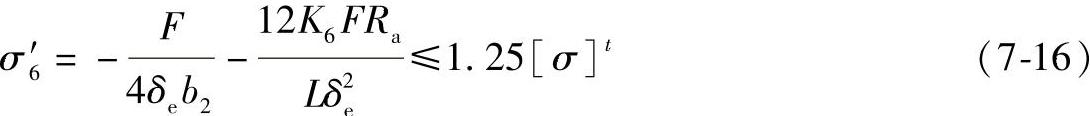
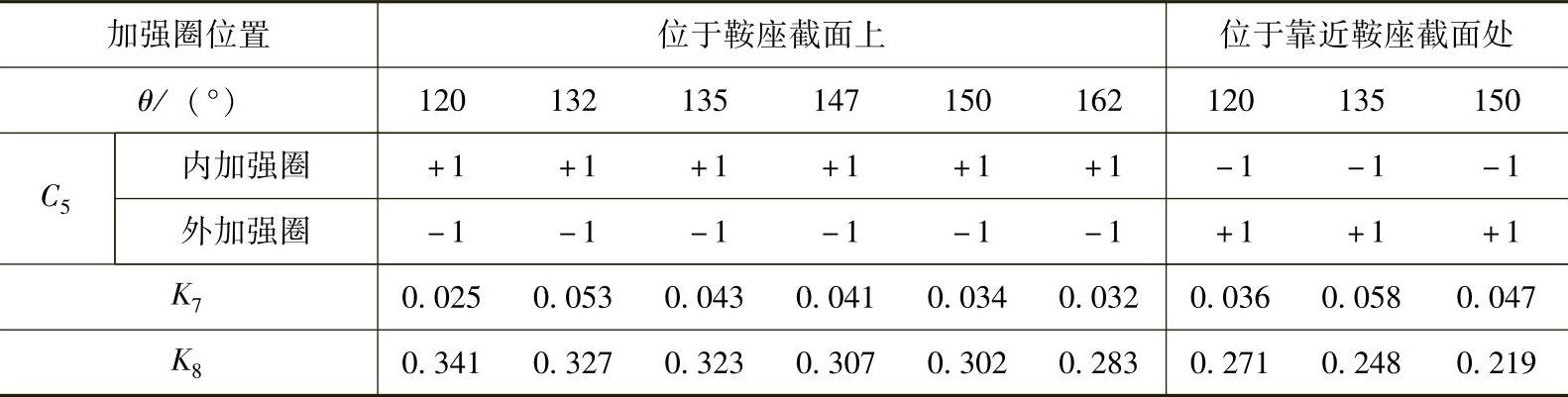
以上式（7-12）～式（7-16）中，系数K₅、K₆列于表7-3中。

表7-3 系数K₅、K₆值（引自JB/T 4731表7-3）

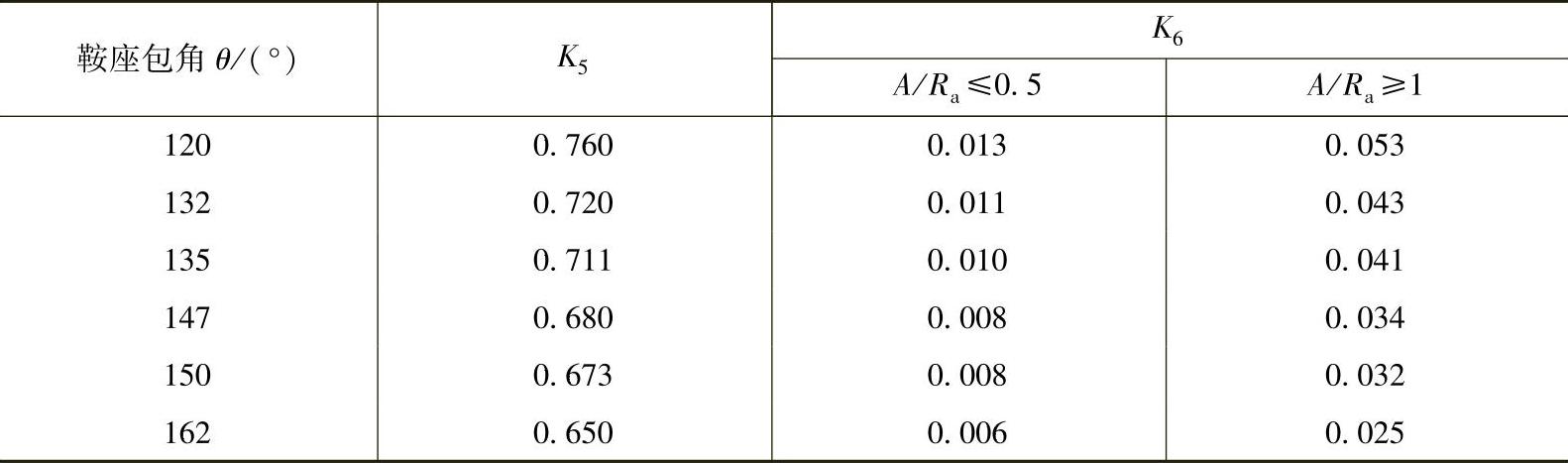
注：当0.5＜A/R_a＜1时，K₆值按表内数值线性内插求取。

2）鞍座截面处设有加强圈的圆筒。鞍座截面处设有加强圈是指加强圈位于鞍座截面两侧各不大于0.5b₂的范围内，见图7-10。此时按图7-11的模型计算加强圈上周向压缩力沿圆筒周向的分布。

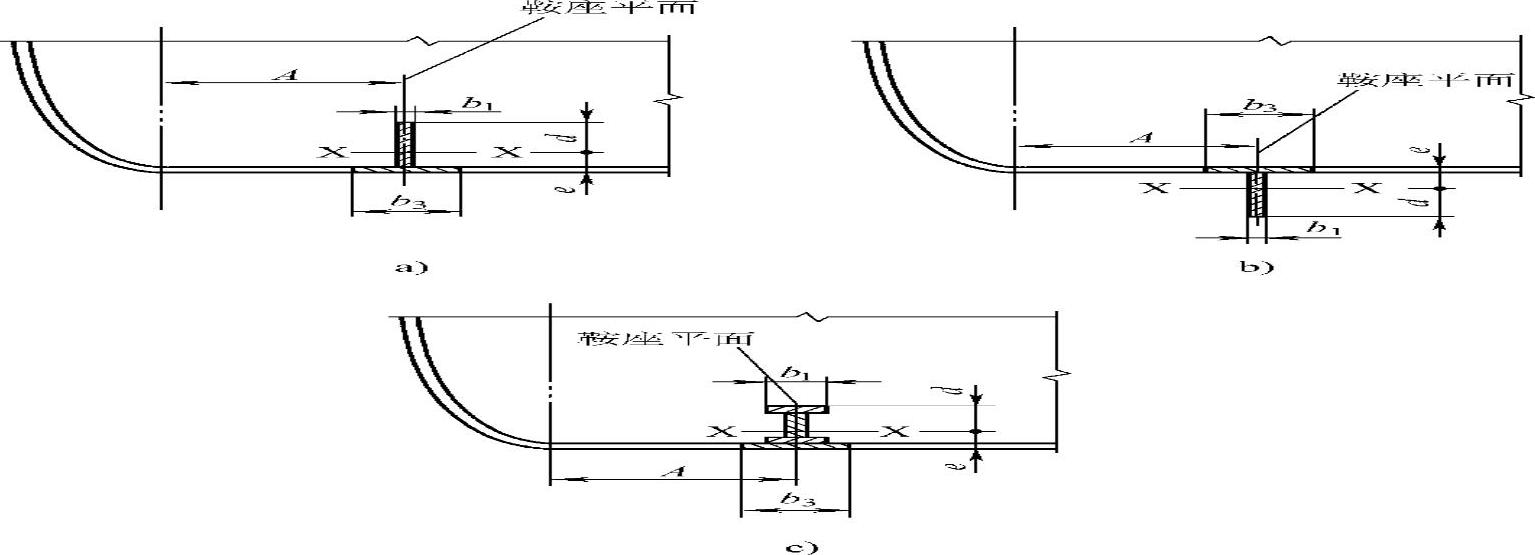
图7-10 在鞍座截面处设有内、外加强圈的圆筒（引自JB/T 4731图7-8）

a）内加强圈 b）外加强圈 c）内加强圈

图7-10中，加强圈横截面高度为（d+e）-δ_e，宽度为b₁；加强圈和圆筒的组合截面高度为d+e，组合截面有效宽度为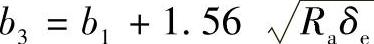。此组合截面的承压截面积A_o和抗弯惯性矩I_o即据这些尺寸计算。

在鞍座边角处圆筒上的周向组合应力：

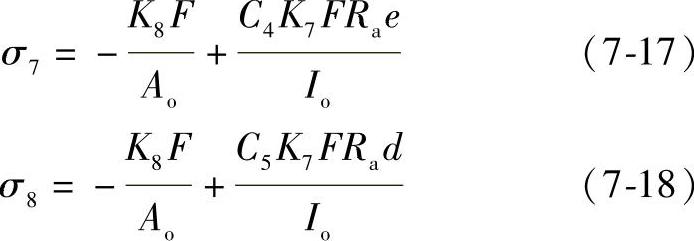
式（7-17）、式（7-18）中，系数K₇、K₈见表7-4；系数C₄、C₅表示加强圈设置在圆筒内侧或外侧时在组合截面的圆筒上所引起弯曲应力为拉伸或压缩的正、负号，也见表7-4；符号e、d表示组合截面形心至圆筒侧顶部或加强圈侧顶部的距离，见图7-10。

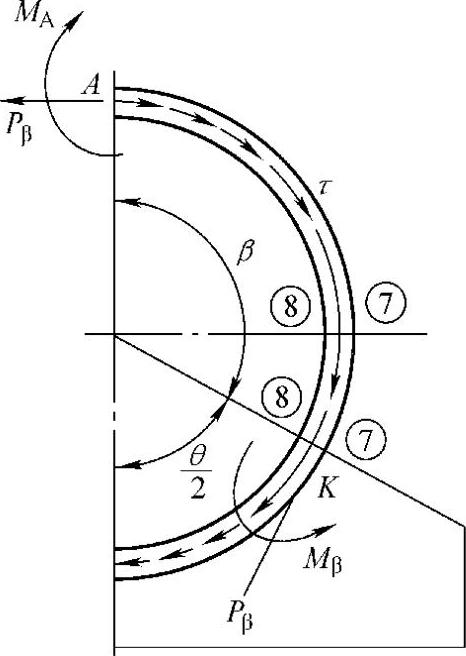
图7-11 加强圈上周向压缩力的计算模型

表7-4 系数C₄、C₅、K₇、K₈（引自JB/T 4731表7-4）

（续）

3）加强圈设在靠近鞍座截面处的圆筒

①无垫板或虽有垫板但垫板尺寸不足，致不能起加强作用时。在圆筒截面最低点处的周向压缩薄膜应力按式（7-12a）计算并校核。在圆筒截面靠近水平中心线处的周向组合应力分别按式（7-17）和式（7-18）计算并校核。但系数K₇、K₈按表7-4中加强圈设在靠近鞍座截面处的值选取。在鞍座边角处的周向组合应力分别按式（7-13a）和式（7-14a）计算并校核。

②有能起加强作用的垫板时。在圆筒截面最低点处的周向压缩薄膜应力按式（7-12b）计算并校核。在圆筒截面靠近水平中心线处的周向组合应力分别按式（7-17）和式（7-18）计算并校核。但系数K₇、K₈按表7-4中加强圈设在靠近鞍座截面处的值选取。在鞍座边角处的周向组合应力分别按式（7-13b）和式（7-14b）计算并校核，并按式（7-15）和式（7-16）计算并校核垫板边缘处的周向组合应力。

（4）鞍座应力计算及校核

1）鞍座由容器自重引起的平均拉伸应力

①当无垫板或垫板尺寸不能起加强作用时

②当垫板能起加强作用时

以上两式中，H_s为计算高度，取鞍座垫板底面至底板底面距离和R_a/3两者中的较小值；b₀为鞍座腹板厚度。

2）鞍座由地震载荷引起的压缩应力。当水平地震力小于等于鞍座底板对基础面之间的静摩擦力时，按下式计算并校核鞍座腹板与筋板组合截面上所引起的压缩应力：

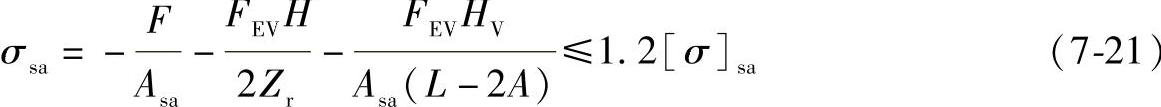
当水平地震力大于鞍座底板对基础面之间的静摩擦力时，按下式计算并校核鞍座腹板与筋板组合截面上所引起的压缩应力：

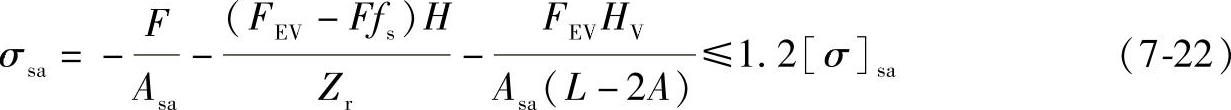
以上两式中，水平地震力F_EV=α₁mg，系数α₁由表7-5查取；H为容器圆筒最低表面至基础表面的距离；H_V为容器圆筒轴线至基础表面的距离；A_sa为鞍座腹板与筋板小端的组合截面积；Z_r为鞍座腹板与筋板小端组合截面的抗弯断面模量；f为鞍座底板对基础表面的静摩擦因数，钢板对钢板时取f=0.3，钢板对水泥时取f=0.4。

表7-5 水平地震影响系数α₁（引自JB/T 4731表7-6）

3）鞍座在容器温度变化时所引起的压缩应力

4）基础螺栓应力计算和校核。受拉侧螺栓的拉伸应力按下式校核：

剪切应力按下式校核：

以上两式中，M⁰_EV-0为倾覆力矩，M⁰_EV-0=F_EVH_V；A_bt为每个螺栓的横截面积；l为圆筒轴线两侧的螺栓间距；n为受拉伸载荷的螺栓数，取总螺栓数的一半；n′为总螺栓数。