材料净用量定额的现场试验验证

在某型号旋转振动模拟平台上验证叶片振动信号重建算法的性能，如图5所示，7支光纤叶尖定时传感器安装按照“5+2”方案分布^[16]，其中5支五均布传感器相互间以72°间隔均匀分布在机匣圆周上，3支三均布传感器以120°间隔均匀分布，两组分布方案有一支传感器可共用。根据直板叶片的尺寸和材料计算出其一阶弯曲振动的固有频率为1810Hz，分析如图6所示叶片在7620r/min转速下气体激振所产生的叶片振动信号。单支叶片定时传感器采样频率等于转速频率127Hz，五均布传感器采样频率为635Hz。

图5 叶片振动参数测量试验平台

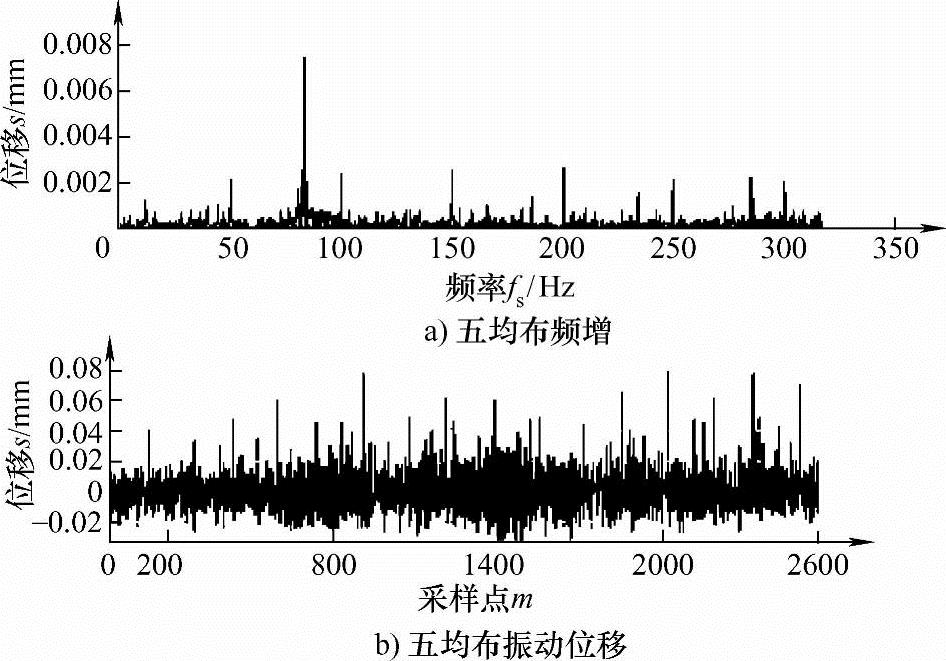
图6 叶片振动五均布采样信号

根据信号频谱可知该转速下叶片振动主要为单一频率的简谐振动，同时伴随有其他频率的干扰信号。由于图6所示五均布传感器采集的振动信号是欠采样信号，无法直观得到其频率信息，通过“5+2”频率辨识法^[1]判断叶片振动频率为1821Hz，由于叶片转动时的振动频率与静止时分析的固有频率相比会随转速升高而增大，因此其结果与先验知识相吻合，可将其作为判断振动信号中心频率的依据。

对采用上述五均布传感器采集的欠采样信号进行叶片振动信号重建，取采样数据长度N=512，中心频率f₀=1800Hz，样条函数阶数n=6，结果如图7所示。

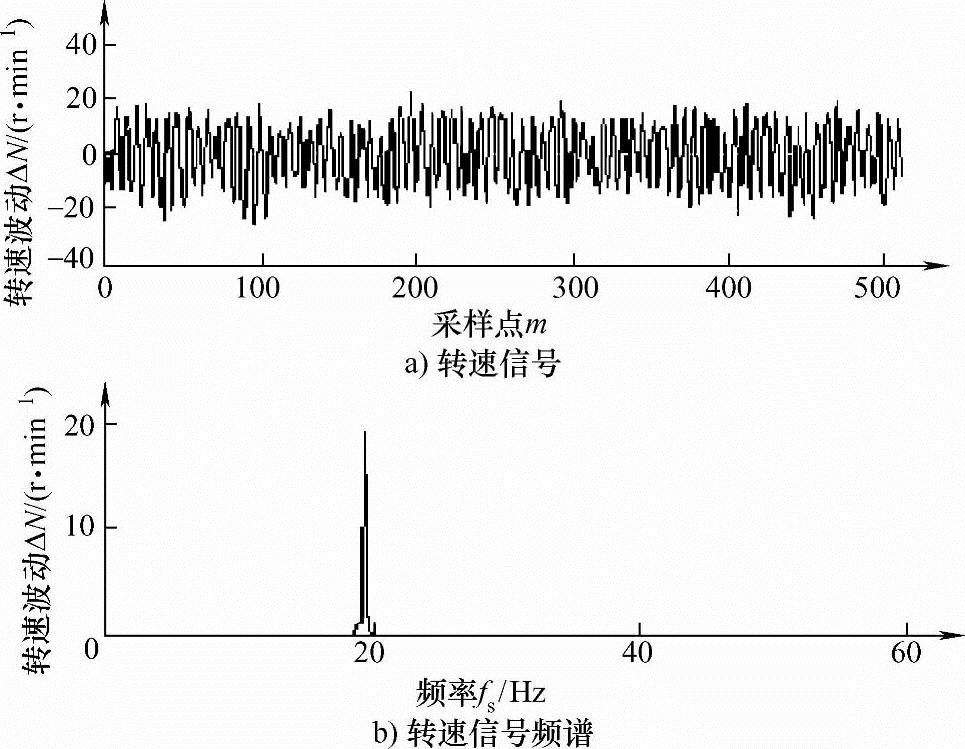
图7 叶片振动重建信号

·五均布采样点 *三均布采样点 ——重建信号(www.xing528.com)

从图7中可见重建信号频谱峰值出现在1890Hz附近，与原辨识频率1821Hz相比有一定偏移。由于传感器采集的信号包含有白噪声成分，信号并非严格带限；另外分析图8所示的采样范围内转速变化曲线，发现转子转速以某一频率成周期性变化，分析原因可能是由转子不平衡等因素引入的。这些都是造成重建信号频域产生误差的原因；在时域内，图7a中“·”表示用于信号重建的五均布采样点，“*”表示三均布传感器采样点，可见重建后的信号准确囊括了三均布采样点的信号，因此它基本反映了叶片振动信号的时域特征，从中可以得到振动瞬时值及峰值等参数。

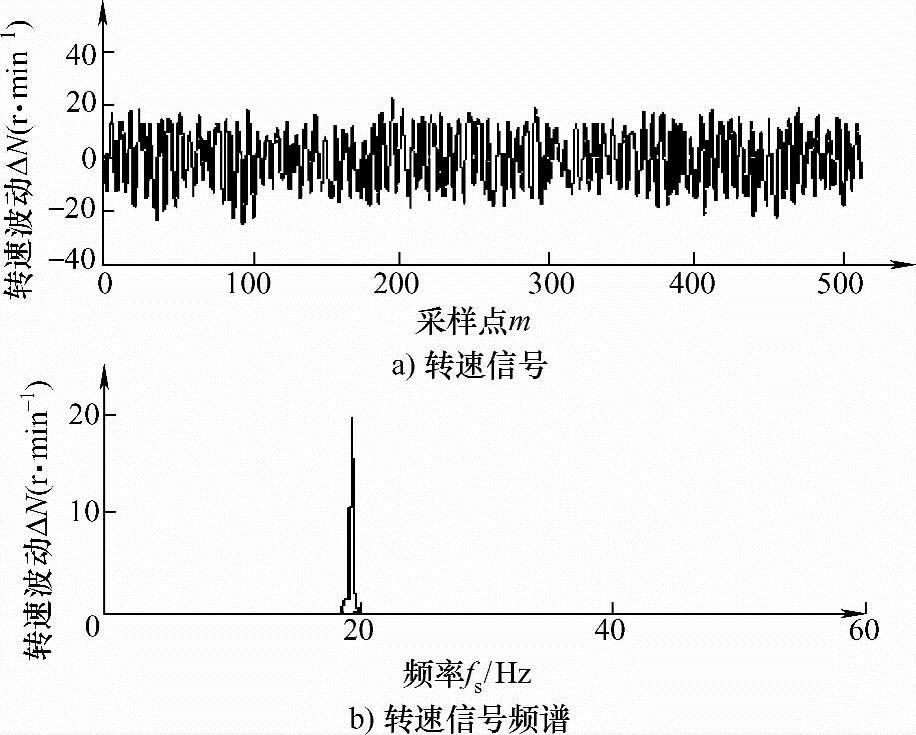
图8 转子转速变化

转子故障诊断依据中的一个关键参数就是叶片振动幅值。通过叶尖定时传感器获取各叶片离散时刻的振动位移，重建得到振动信号波形，重建时域范围内的峰值作为该转速下的振动幅值，观察叶片间振幅分布，分析振动模态可以得到转子失调等故障信息。通过改变图5所示试验台转子部分叶片厚度可构建不同的振动特征，利用有限元模型仿真叶盘受迫振动响应的差异和规律，在只改变4号叶片厚度的情况下振动一阶模态分布如图9所示。根据实测信号重建不同转速范围的叶片振幅如图10所示。

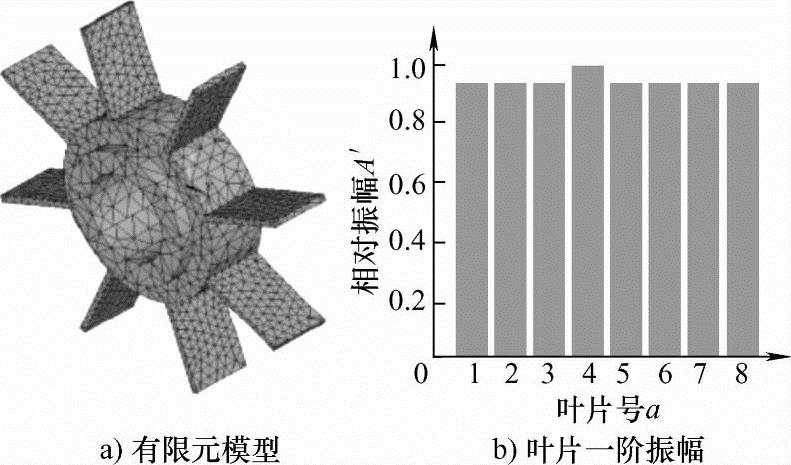
图9 叶盘有限元仿真

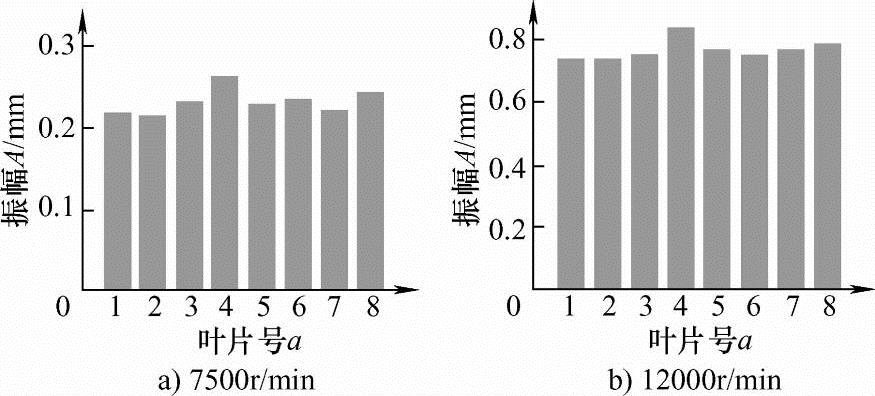
图10 不同转速下的叶片振动重建信号振幅

图9所示的有限元分析是在转子静止状态下得到的，旋转状态下叶片响应会存在一定偏移，这是由转子的动频特性和叶片错频技术等因素造成的。仿真中受迫响应振幅最大的是厚度改变的4号叶片，图10中不同转速下的叶片受迫振动重建信号峰值最大的也是4号叶片，结论与理论分析吻合。利用插值算法的振动信号重建能准确反映故障叶片振动幅度的比例关系，为测量转子失调等故障特征提供了依据。