面向对象的不确定度分析方法

蒙特卡罗法是一种概率事件仿真技术，其核心是以变量的伪随机抽样获得服从特定概率分布的随机数，并以此模拟测量过程中的各种随机误差，产生可能的结果分布。这种评价方法通过大量简单重复的抽样来实现复杂函数的计算，容易求解，不受函数关系是否线性的限制，避免用户增加过多的投入成本，特别适合于大尺寸测量的不确定度准确评价。面向对象的不确定度求取步骤如下：

1）建立大尺寸测量仪器中各个传感器的测量模型以及拟合任务模型。

2）确定影响精度的所有误差分量以及各自的分布类型及其特征量，包括各传感器和环境影响等误差源的误差模型建模，给每个误差源一个合适的概率分布函数。

3）按照各误差源的概率密度函数分布随机抽样，模拟测量误差，求出各传感器的输出结果。

4）根据1）中建立的拟合模型计算最终拟合结果。

5）重复3）和4），进行n次仿真，得到描述最终拟合任务概率密度函数和n个样本结果。计算该样本的标准差，用于评价最终面向对象的不确定度。

另外，数值表达方式是枯燥的，而本方法将样本利用计算机可视化技术展现出来，形成离散点云提供给用户直观的观察。本文以工业上常见的激光跟踪仪测量圆形截面为例，介绍测量圆心和半径的不确定度。激光跟踪仪是较理想的大尺寸测量仪器，测量范围可达到35m。首先建立测量模型。激光跟踪仪内部共3个传感器，为一个激光干涉测距单元和两个测角单元，分别为水平角α和垂直角β。利用球坐标得到三坐标

暂不考虑周围环境等的误差源，建模3个传感器的误差源：(www.xing528.com)

式中，ε_l～N（0，10μm+0.8μm/L）；ε_α、ε_β～N（0，1″）。

拟合圆的公式为

仿真表明，样本数过少不能得到足够的统计来表达真实不确定度，样本数过多会增加不必要的计算负担。本文取样本数为n=500。对每个样本中的点分别拟合，得到一组参数a、b、r。对这组参数统计得到最终面向任务的不确定度，即拟合圆心的不确定度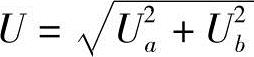和拟合半径不确定度U_r。

图1 圆心拟合不确定度 Fig.1 Uncertainty of circle center

仿真假设激光跟踪仪放在圆心处，测量直径为15m的圆形截面工件。设圆截面已投影在xy平面，共测量如图1中的4个测量点，其相对x轴对称分布。

图1为拟合不确定度。为了方便，将其中可视化点云放大了5000倍。例如图中的P₁～P₄为测量点的不确定度，可明显看出激光跟踪仪测量的不确定度特性，在径向距离上的不确定度较低，而横向测量不确定度较高。这是因为激光跟踪仪测距单元为干涉仪，精度高，而测角精度稍低。圆心的不确定度特性也一目了然，拟合x轴的不确定度较大，是因为测点相对x轴不对称；而y轴不确定度较小，是由于测点相对y轴对称。