【摘要】：设标定参照物平面位于空间坐标zw=0上，图像平面与二维靶标平面在映射变换，即式中，为摄像机内部参数矩阵；u0、v0为摄像机的主点坐标；m=T和为空间任意一点P在图像平面和世界平面坐标；hi为3×3投影矩阵H的第i列；ri为旋转矩阵R的第i列；t为平移向量。优化模型表示为通过式，采用Levenberg-Marquardt非线性优化算法，可以得到摄像机所有内部和外部参数。
设标定参照物平面位于空间坐标zw=0上，图像平面与二维靶标平面在映射变换，即
式中，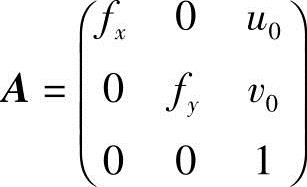
为摄像机内部参数矩阵；u0、v0为摄像机的主点坐标；m=（uv 1）T和
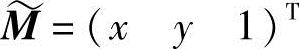为空间任意一点P在图像平面和世界平面坐标；hi为3×3投影矩阵H的第i列；ri为旋转矩阵R的第i列；t为平移向量。
根据标定参照物上特征点的图像坐标和其对应的世界坐标，采用线性或者非线性最小二乘法解出投影矩阵H，根据r1、r2的正交性，有
设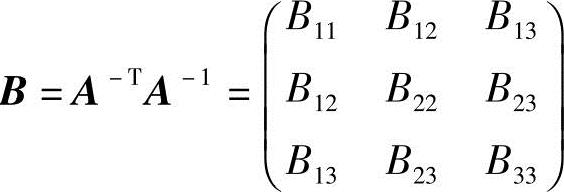
，根据式（5）变换求解可得内部参数和外部参数为
式（4）表示理想无畸变情况下图像坐标与特征点空间坐标的变换关系。在高精度视觉测量中，必须考虑成像系统复杂的畸变影响。考虑径向和切向畸变的摄像机畸变模型是在理想针孔透视模型上的扩展，径向和切向畸变可分别近似表示为(www.xing528.com)
式中，Xu、Yu为原点在像面中心的理想图像坐标；r2=X2u+Y2u；k1、k2、p1和p2为畸变系数。则实际帧存坐标可以表示为
标定时，靶标上的特征点经透视变换投影到像面上，得到模型图像坐标（Ui，Vi），与实际由图像处理得到的特征点图像坐标（ui，vi）不一致，存在偏差，建立优化数学模型以使这种偏差最小[11]。优化模型表示为
通过式（10），采用Levenberg-Marquardt非线性优化算法，可以得到摄像机所有内部和外部参数。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
