【摘要】：设左摄像机坐标系为Olxiyizi，图像坐标系为OiXiYi，x、y方向有效焦距分别为ftx、fty；右摄像机坐标系为Orxryrzr，图像坐标系为OrXrYr，x、y方向有效焦距分别为frx、fry；系统测量坐标系σxsyszs与左摄像机坐标系重合。则测量系统坐标系与右摄像机坐标系间的相互位置关系可以用空间转换矩阵Msr表示为图1 立体视觉传感器三维测量模型 Fig.1 3-D measurement model of stereo-visual sensor式中，，，分别为坐标系σxsyszs与Orxryrzr间的旋转矩阵和平移矢量。
立体视觉传感器的数学模型如图1所示。设左摄像机坐标系为Olxiyizi，图像坐标系为OiXiYi，x、y方向有效焦距分别为ftx、fty；右摄像机坐标系为Orxryrzr，图像坐标系为OrXrYr，x、y方向有效焦距分别为frx、fry；系统测量坐标系σxsyszs与左摄像机坐标系重合。则测量系统坐标系与右摄像机坐标系间的相互位置关系可以用空间转换矩阵Msr表示为
图1 立体视觉传感器三维测量模型 Fig.1 3-D measurement model of stereo-visual sensor
式中，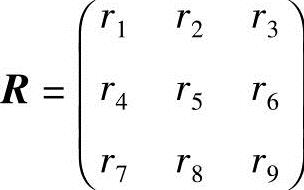
，
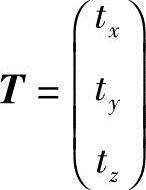，分别为坐标系σxsyszs与Orxryrzr间的旋转矩阵和平移矢量。
设空间任意一点P在σxsyszs的坐标为Ps=（xsyszs）T，在Orxryrzr的坐标为Pr=（xryrzr）T，在左右摄像机图像平面上的投影点分别为pl、pr，对应的归一化齐次坐标分别为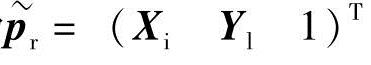
和
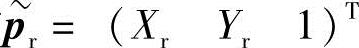，根据摄像机透视投影模型(www.xing528.com)
根据式（1）表示的传感器位姿变换关系和式（2）表示的摄像机透视变换模型，立体视觉三维测量数学模型可以表示为
已知空间点在左右摄像机中的归一化图像坐标以及传感器结构参数中旋转矩阵R和平移矢量T就可以得到被测物体点的三维空间坐标。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
