聚丙烯纤维在电池隔膜中的重要应用及标定结果分析

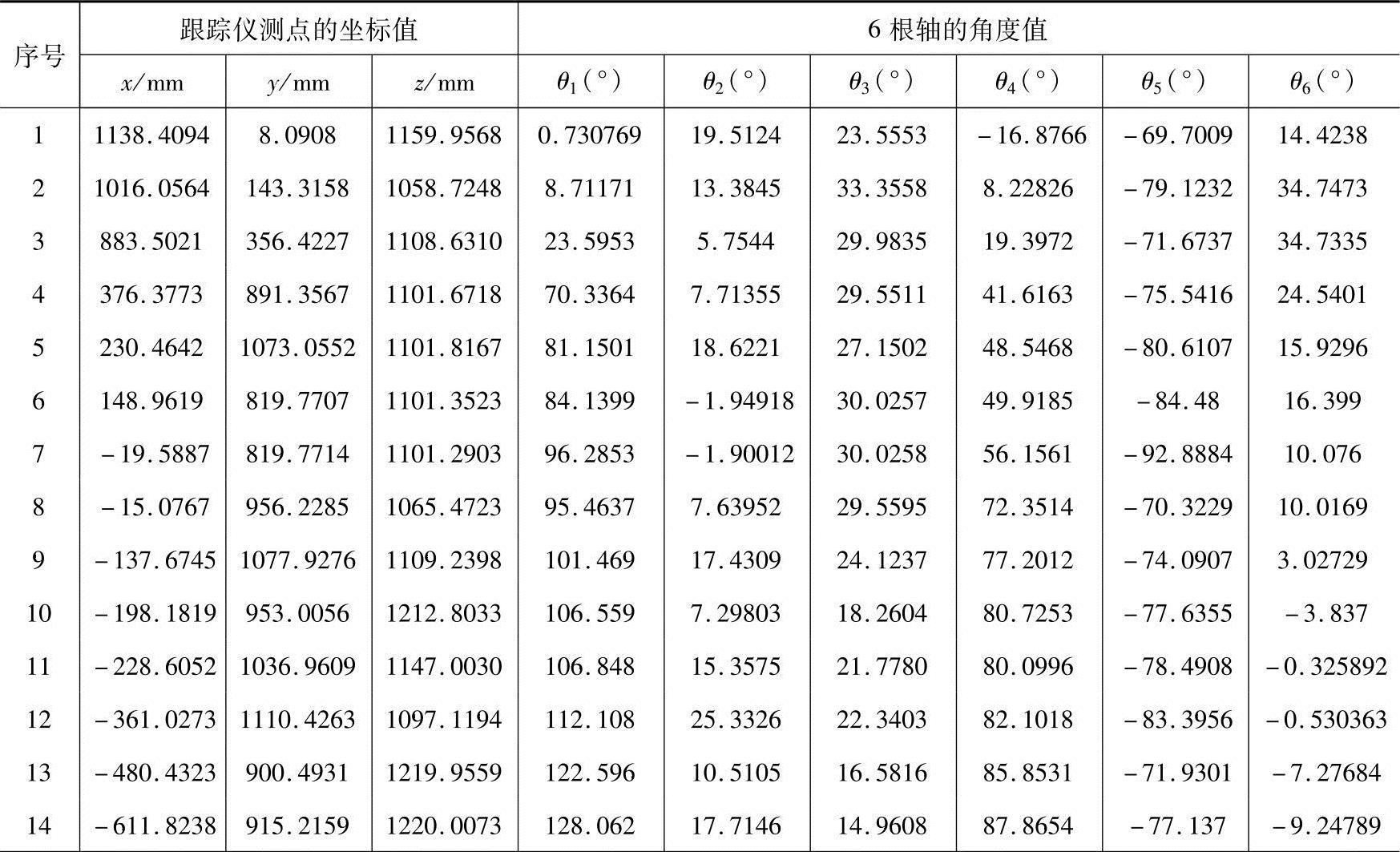
试验所用主要设备如图5所示，在标定试验过程中，测量了空间的20个点，目标点为末端凸缘盘的中心点，并通过串口通信取得机器人6根轴的角度值，如表2所示。用其中的后15个点建立矩阵方程，另外的前5个点来验证结果。

将6根轴的角度值带入式（16）即可求得末端凸缘盘中心点在机器人基坐标系下的理论位置，将其与表2中的用跟踪仪测量的坐标值相减，即可求得机器人的位置偏差ΔP（相当于式（7）中的b）。将角度值带入式（8）可以求得系数矩阵A，从而根据式（11）求得机器人连杆参数修正值。

图5 试验设备现场

用Matlab进行解算，解算结果为

ΔX=（a₁a₂a₃a₄a₅a₆d₁d₂d₃d₄d₅d₆）

=（99.395 706.064 133.634 0.187 -0.312 0.062 615.507-0.099 -0.099 756.071 -0.096 84.233）

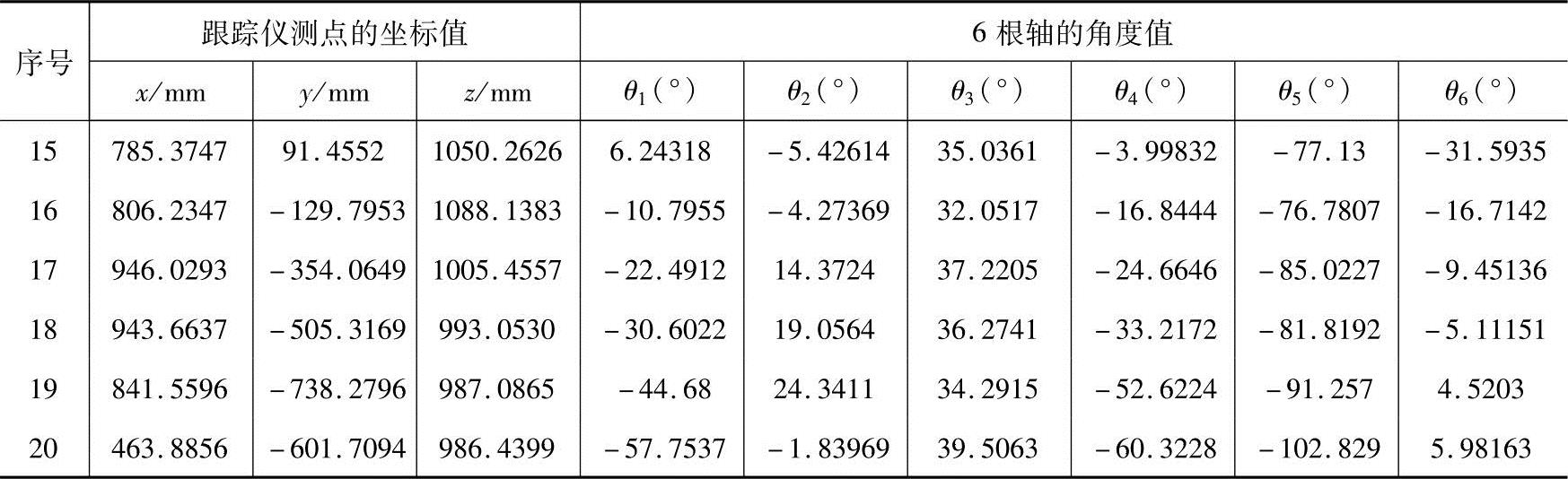
表2 跟踪仪测量值和机器人角度值

（续）(www.xing528.com)

对于前5个点，修正前后的末端凸缘盘中心点在机器人基坐标系下的坐标值如表3所示。将表2、表3中的跟踪仪测点的前5组数据对比，可得到修正前后的误差，如表4、表5所示。

表3 修正前后中心点在机器人基坐标系下坐标数据

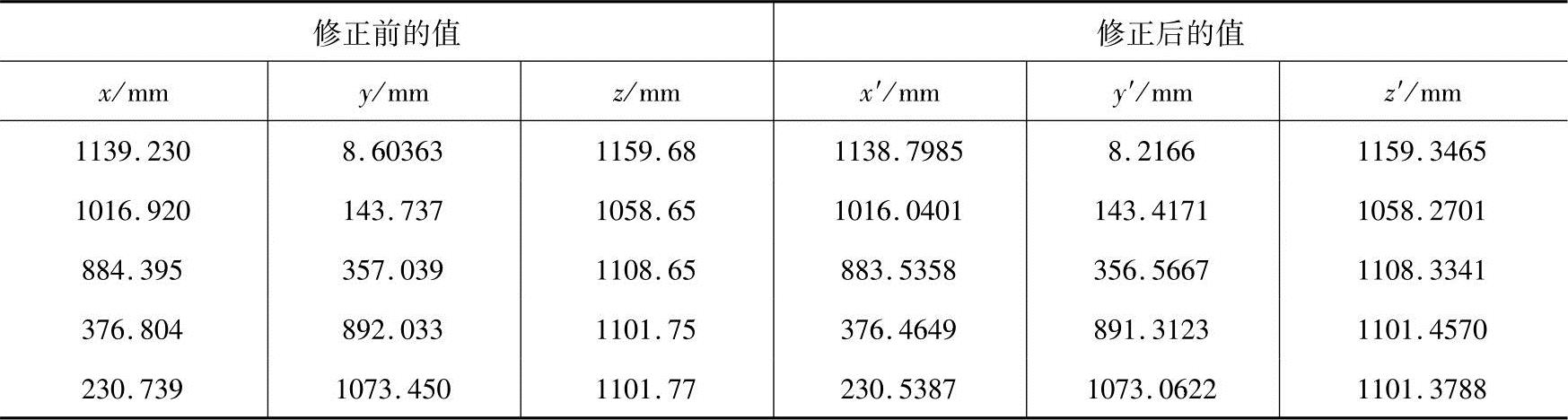
表4 修正前跟踪仪器点误差

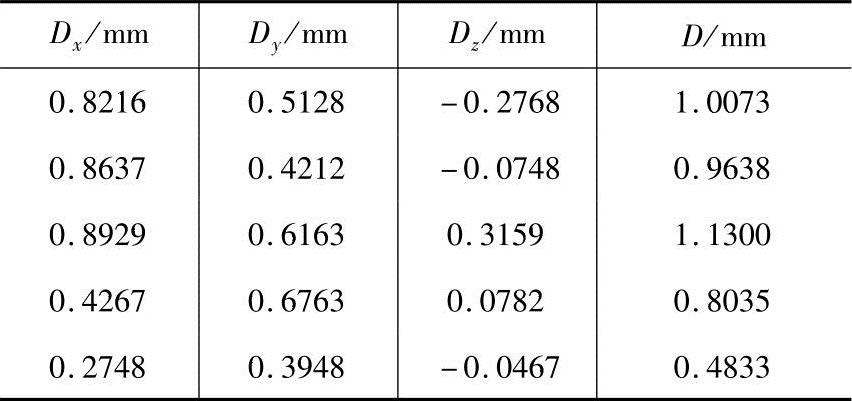
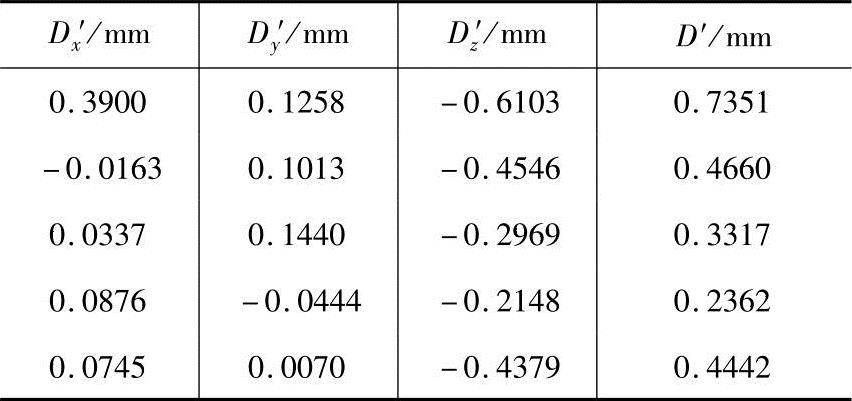
表5 修正后跟踪仪器点误差

可以看出标定后，机器人的定位精度得到了明显的改善，标定前定位精度D的平均误差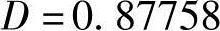、标准方差S²=0.2495；修正后，定位精度D的平均误差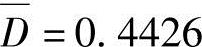，标准方差S²=0.1878，精度提高了一倍。而且通过表2～表5中数据可以看出x、y、z的单方向的跳动值（最大最小值的差）由原来的0.6181、0.2815、0.5927减小为0.4063、0.1884、0.3955。由于在采集数据的过程中，激光跟踪仪需要从反射靶球接受返回的激光。机器人在z方向的运动范围受到限制，因而训练数据的z方向范围空间太小，训练数据的样本空间遍历性不够，导致修正后表5中D_z′列数据有所增加。