机器人位置误差标定原理

IRB2400机器人是一种开环运动结构，通过角度测量装置可以确定每根轴的角度值。在每根轴上建立相应的齐次方程而构建机器人的运动模型，就可以确定机器人的末端位置和姿态（相对于机器人的基座）。由于机器人的各个连杆参数和角度参数存在一定误差，从而导致了机器人的末端位姿不准确。为了简单起见，仅就位置误差进行标定。

确定机器人每根轴的齐次变换矩阵需要连杆长度a、连杆偏置d、连杆扭角α、轴的转角θ这4个参数。通过将这些齐次矩阵联乘，就可以确定机器人末端的位姿P为

P=F（a，d，α，θ） （1）

由于连杆转角通过轴的角度测量装置来获得，其他3个参数由机器人生产和装配工艺确定，必然存在误差，而导致a、d、α、θ存在误差Δa、Δd、Δα、Δθ，机器人末端实际位姿是

P′=F（a+Δa，d+Δd，α+Δα，θ+Δθ） （2）

ΔP=P-P′ （3）

当这些误差都比较小时，可以简化成相应的线性方程

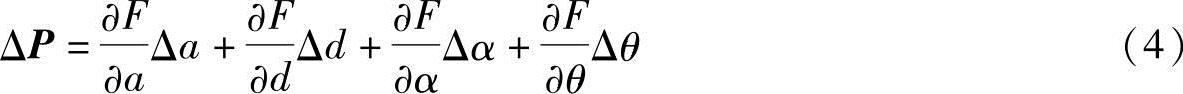
对于6R机器人IRB2400，式（4）中∂a可以代表∂a₁、∂a₂、∂a₃、∂a₄、∂a₅、∂a₆，∂d、∂α、∂θ同此约定。由于在建立运动学方程的过程中带入未知角度来求解系数矩阵比较复杂，为了简化问题，将用测量所得的连杆扭角值来代替理论的连杆扭角值（方法见第3.2、3.3节），同时认为通过机器人码盘读取的每根轴的转角值不存在误差，也即认为式（4）中的后两项的微变化量Δα、Δθ为0，所以式（4）可以变换为

由于机器人IRB2400存在6个连杆长度参数和6个连杆偏置参数，根据式（5）可以得到空间任一位姿P_i时的方程(www.xing528.com)

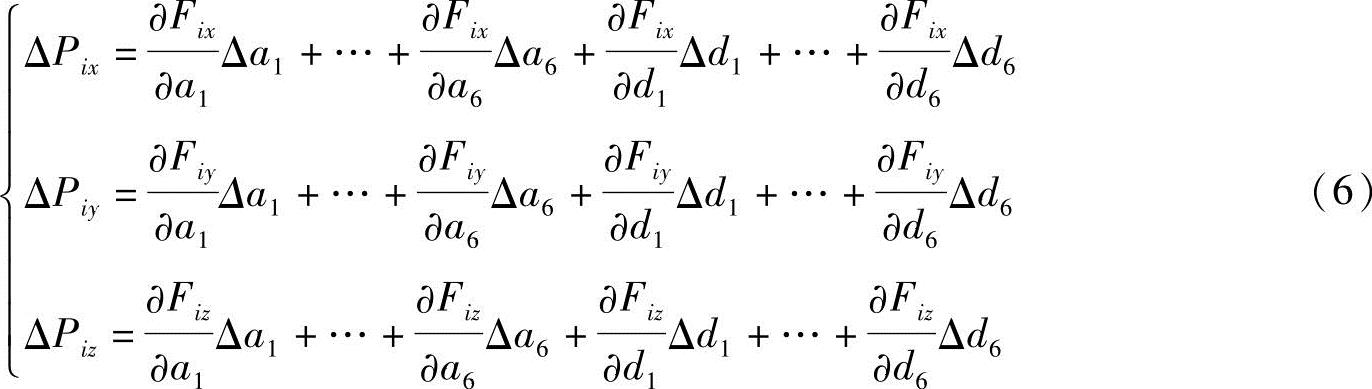
式中，ΔP_ix、ΔP_iy、ΔP_iz为P_i在x、y、z三个方向上的偏差。

若测量了空间中n个点的坐标，将会得到式（7）（也即将式（6）转换为矩阵形式）

AΔX=b （7）

只在保证n取得足够大，就可以利用最小二乘法求得ΔX的最佳值

ΔX=（A^TA）-1A^Tb （11）

在式（11）中，A是关于6根轴角度的函数，是常见的雅可比矩阵的一种变形形式，b是偏差矩阵。

将所求的连杆参数误差ΔX加到机器人给出的连杆参数上，就可以得到新的一组连杆参数，根据这些新的连杆参数重新求解误差，反复进行迭代，直到ΔP_x、ΔP_y、ΔP_z足够小为止。为此，只要能够实际测量出机器人控制点在机器人基坐标系下的偏差值ΔP，也即b，就可以通过式（11）来求解机器人的连杆参数，从而达到标定的目的。