标定位置摄像机外参估计优化方案

2.2.1 外部参数的直接计算

系数矩阵A是基于共面摄像机成像模型，采用二维共面靶标标定的结果，其中摄像机的外部参数可以在已知摄像机内部参数的条件下提取出来。将矩阵A前乘F和V得到

Q=F^-1V^-1A=λRT （2）

矩阵Q表征了摄像机的位置关系和比例因子λ′将Q以列矢量的形式表示为

由此可得

λr₁=q₁λr₂=q₂ （4）

比例因子近似为

λ=（‖q₁‖+‖q₂‖）/2

式中，‖·‖为向量的模。由此旋转矩阵的前两个矢量近似为(www.xing528.com)

因为摄像机的内部参数和比例因子仅是一个近似值，因此求出的旋转矩阵的列矢量的正交约束并不能完全满足，所以需要对求出的列矢量进行归一化处理

由旋转矩阵R列矢量的正交约束得到r₃=r₁×r₂。获得旋转矩阵R后，可以求得平移矩阵

在估计的摄像机内部参数的条件下，基于共面成像模型，可以直接求得摄像机在各个标定位置的外部参数，这些参数表示了摄像机与各个标定位置的靶标的相对位置关系。

2.2.2 外部参数的优化

摄像机内部参数实际上不是摄像机的真实值，根据估计的内部参数直接计算的旋转和平移参数只是摄像机外部参数的一种近似，因此还必须求得摄像机外部参数的优化值。

假设O_j=（u_j，v_j）为直接测量的靶标特征点坐标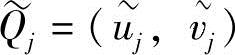；为根据摄像机模型计算得到的相应坐标，建立优化的目标函数。

将直接计算的摄像机外部参数作为优化的初始值，通过迭代可求得各个标定位置摄像机的外部参数。