【摘要】：图3 光平面与棱线不垂直时误差示意图下面分析调整误差给标定带来的影响。假定运动方向已平行光平面但光平面与棱线不垂直。可用图3表示，设棱线间距为d，光平面与棱线相交形成的线段长为d′，垂直误差角为Δθ，则d′=d/cosΔθ，有Δd′=d′-d=d≈dΔθ2。当一维工作台运动方向不与光平面平行时，考察工作台移动位移，与棱线在光平面的实际位移关系，如图4所示。因此ΔS′也是二次项误差。
调整时，通过移动工作台观察在整个移动范围内光条折线在齿型靶上的位置，应保证折线在齿型靶上的位置不变，此时说明光平面已与基面相垂直，如果光平面与齿型靶上边沿及下边沿的交点的xc坐标值相同（可用标记方法，通过图像观察），则可保证光平面与Ocyc轴平行。经这样调整后光平面与棱线垂直。
图3 光平面与棱线不垂直时误差示意图
下面分析调整误差给标定带来的影响。假定运动方向已平行光平面但光平面与棱线不垂直。可用图3表示，设棱线间距为d，光平面与棱线相交形成的线段长为d′，垂直误差角为Δθ，则d′=d/cosΔθ，有Δd′=d′-d=d（1-1/cosΔθ）≈dΔθ2。因此Δθ对d′的影响是二次误差关系，对标定结果影响很小。即使Δθ=2°，d′才有0.00061d的误差。
当一维工作台运动方向不与光平面平行时，考察工作台移动位移，与棱线在光平面的实际位移关系，如图4所示。设移动前棱线与光平面交于C点，移动后与光平面交于D点，移动距离为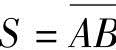
，令S′=CD，设运动方向与光平面夹角为Δa，则S′=S/cosΔα，同样有ΔS′=S′-S≈S（Δα）2。因此ΔS′也是二次项误差。(www.xing528.com)
图4 运动方向不与光平面平行时误差示意图
由上述分析可见，标定时不要求很高的调整准确度。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
