MATLAB模糊控制器设计优化

MATLAB推出的模糊逻辑工具箱（Fuzzy Logic Toolbox）是进行模糊控制器设计的一个有效工具箱，利用此工具箱对模糊控制器进行具体设计^[8]。

模糊控制器的设计主要包括：控制参量的确定、变量的模糊化、隶属度函数的确定、模糊控制规则的建立及解模糊判决。MATLAB模糊逻辑工具箱提供了五个基本的图形用户界面（GUI）来设计模糊控制器，可直观地完成模糊控制器的设计，它们分别是：模糊推理系统（FIS）编辑器、隶属度函数编辑器、规则编辑器、规则观察器和曲面观察器。五个基本GUI之间是动态链接的，其运行界面如图7-7所示。

图7-7 模糊系统主界面

1.控制参量的确定

由前面的分析可知，电弧弧长变化大小受送丝速度v_f的影响。模糊控制器的主要功能是通过在线监测反馈电弧电压U_f，通过模糊控制器输出调节送丝驱动电路中晶闸管触发时间长短的电压，使得送丝电动机驱动电压发生变化，从而改变电动机的转数，控制送丝速度v_f，来维持弧长的稳定。因此选择反馈电弧电压U_f的偏差E和偏差变化率EC作为模糊控制器输入变量，调节晶闸管触发时间长短的电压U为控制器输出变量。

2.变量的模糊化

变量的模糊化过程，主要是通过测量输入变量的值，并将其转化为通用语言值表示的某一限定码的序数，每一个限定码表示论域里的一个模糊子集，并由其隶属度函数来定义。对模糊控制器的输入变量作以下定义：

e_n=U_g-U_fn

ec_n=e_n-e_n-1 （7-18）

式中 e_n——第n次的采样偏差；

U_g——电弧电压给定量；

U_fn——第n次采集到的电弧电压反馈量；

ec_n——第n次的偏差变化率；

e_n-1——第n-1次的采样偏差。

实际焊接中弧长波动一般不超过±2mm，根据在埋弧焊情况下电场强度为30V/cm^[9]，由此可得输入量的偏差范围为：e_n=-0.2×30～0.2×30≈-6～6V。

选定e_n的变化范围为[-6，6]，同样ec_n的变化范围也为[-6，6]。

偏差E、偏差变化率EC和输出控制量U的模糊集和论域选取如下：

取E、EC、U的论域皆为[-6，6]，分为十三级，即

E={-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}

EC={-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}

U={-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}

在各论域E、EC、U的语言变量取七个语言值：负大（NB）、负中（NM）、负小（NS）、零（ZO）、正小（PS）、正中（PM）、正大（PB），分为七档，即

E={NB、NM、NS、ZO、PS、PM、PB}

EC={NB、NM、NS、ZO、PS、PM、PB}

U={NB、NM、NS、ZO、PS、PM、PB}

根据偏差、偏差变化率及输出量的取值范围和它们的论域，可求出偏差e的量化因子k_e、偏差变化率ec的量化因子k_ec和输出量u的比例因子为

k_e=6/6=1

k_ec=6/6=1

k_u=6/6=1 （7-19）

3.隶属度函数的确定

隶属度函数形状可取为三角形、梯形、钟形或正态分布。为了保证所有论域内的输入量都能与某一模糊子集相对应，模糊子集的数目和范围必须要遍及整个论域，对每一个输入量，至少有一个模糊子集的隶属度大于零。在隶属度函数的选择方面，已有经验表明，通常选用三角形和梯形函数的隶属度函数在实际应用中带来很多方便^[7]。

以三角形曲线形状隶属度函数为例，模糊量E、EC、U的隶属度函数表达式形式为

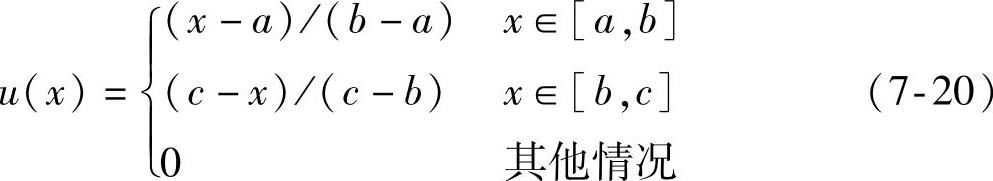
式中 a、b、c——三角形参数。

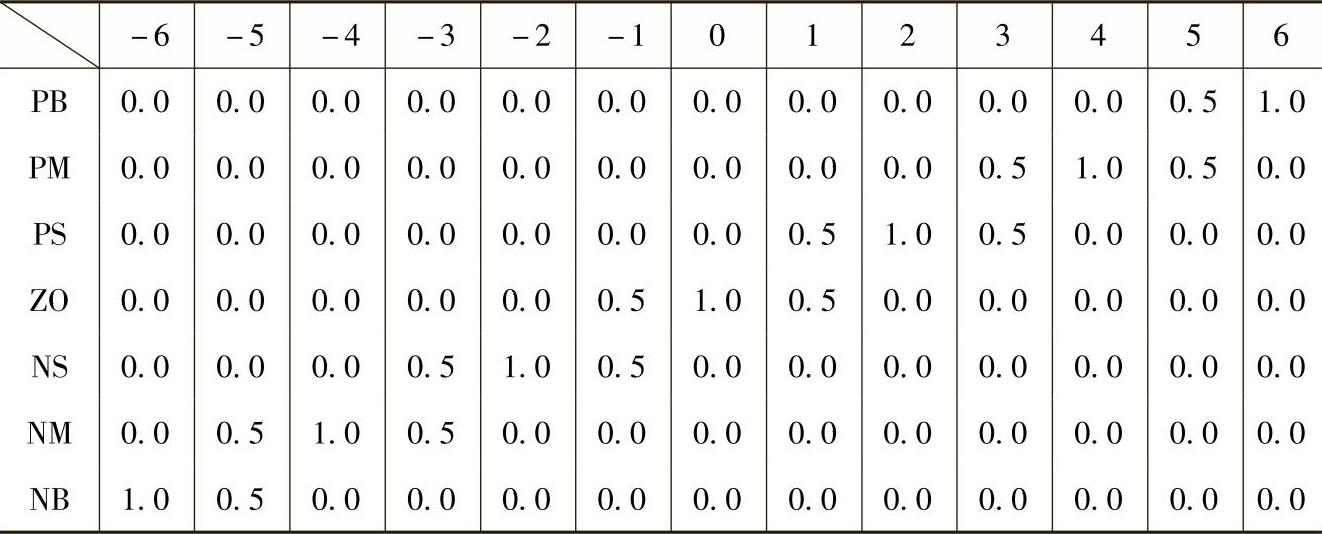
由MATLAB模糊逻辑工具箱隶属度函数编辑器编辑的E、EC、U隶属度函数曲线如图7-8所示，隶属度见表7-1。

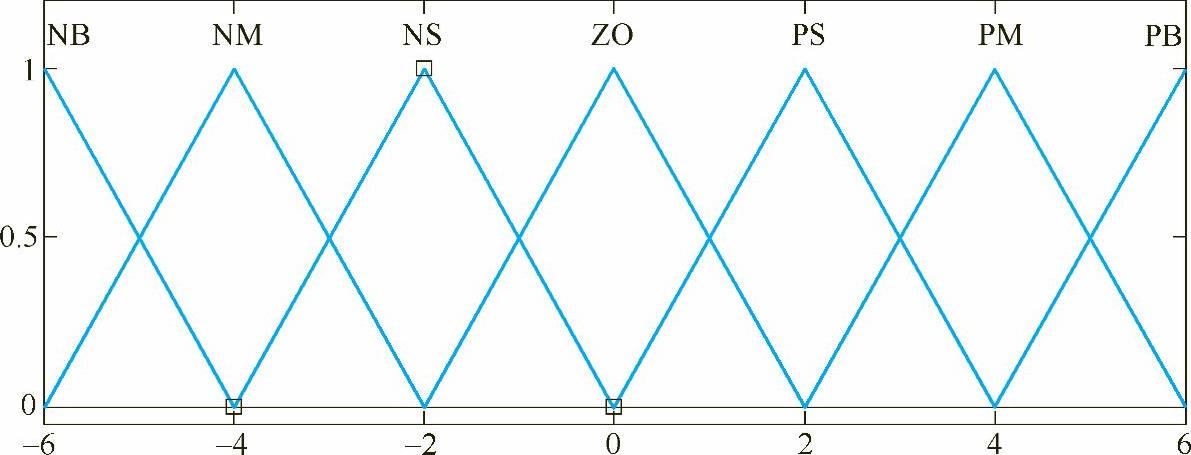
图7-8 偏差量E、偏差变化率EC、输出量U的隶属度函数

表7-1 偏差量E、偏差变化率EC和输出量U的隶属度

4.模糊控制规则的建立

采用弧压偏差和偏差变化率作为输入量，可以保证控制系统的稳定性，减少超调和振荡。逻辑推理决策实质是模糊逻辑推理，它是以模糊判断为前提，运用模糊语言规则推出近似模糊判断结论的方法。控制规则的建立采用较为成熟的Mamdani（Max-Min）推理算法，其基本设计原则为：当偏差较大时，以消除偏差为主，当偏差较小时，则以系统稳定、消除振荡和防止超调为主^[10-13]。模糊控制器的模糊控制规则具有如下形式：

IF{E=A_i，EC=B_i}THENU=C_i，i=1，2，…，7(www.xing528.com)

式中 A_i、B_i和C_i——各自论域上的模糊语言值（如NB、NM等）。

由每条IF-THEN控制规则可得一个三元模糊关系：

R_ij=（E_i×EC_j）U_ij （7-21）

相应的隶属度函数为

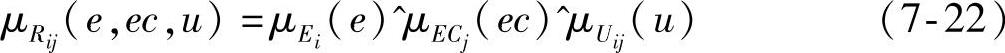
∀e∈E，∀ec∈EC，∀u∈U。

采用Max-Min推理合成算法有

相应的隶属度函数为

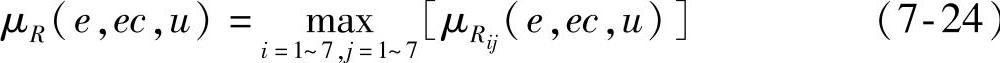
根据输入E和EC，可求得输出控制量U：

U=（E×EC）R （7-25）

相应的隶属度函数为

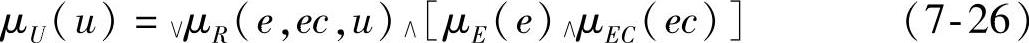
∀e∈E，∀ec∈EC，∀u∈U。

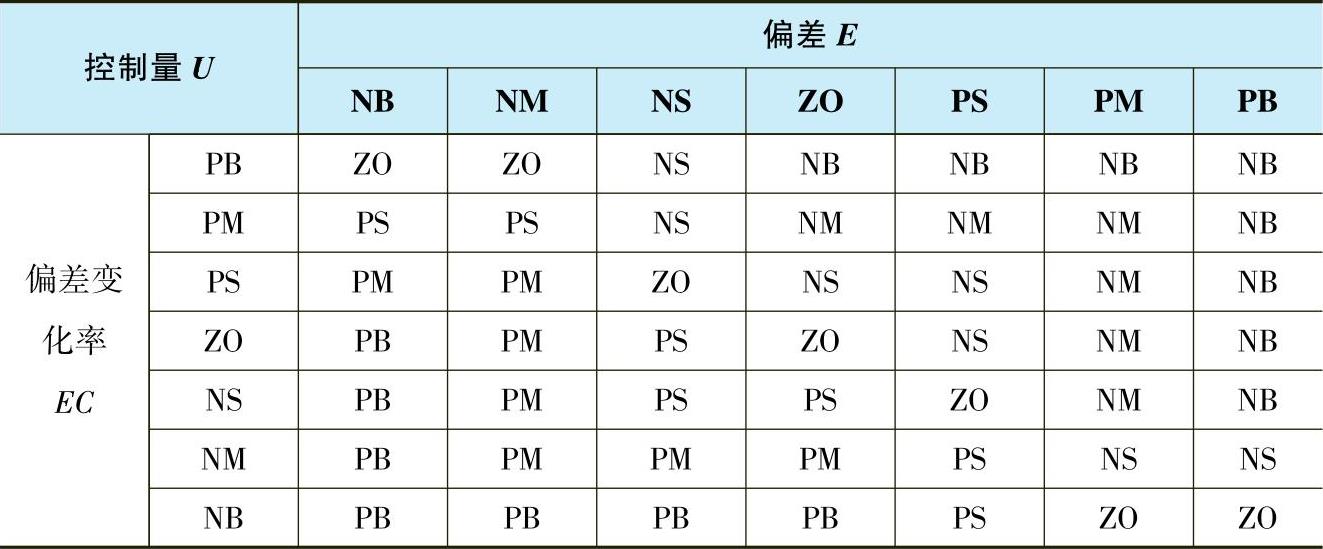
根据系统工作的特点，取每条模糊控制规则的权重皆为1，按上述推理方式可归纳出7×7=49条规则，见表7-2。

表7-2 模糊控制规则表

5.解模糊判决

通过模糊推理得到的模糊集合，必须要经过解模糊判决过程，才能得到一个精确值去执行控制过程。目前常用的解模糊判决方法有重心法、平均最大值法、最大隶属度法。其中重心法的控制精度最高、稳态性能好，所以选用重心法进行精确量的解模糊判决。重心法就是取模糊隶属函数曲线与基础变量轴围成面积的重心所对应的基础变量值作为确定值的方法。其计算公式为

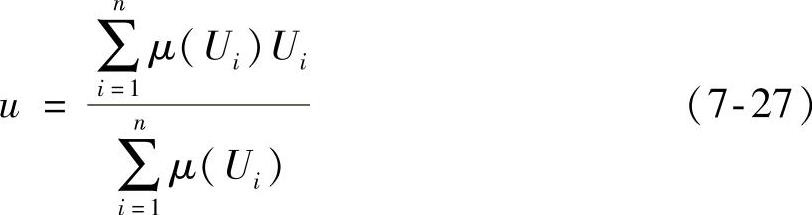
6.模糊控制表的生成

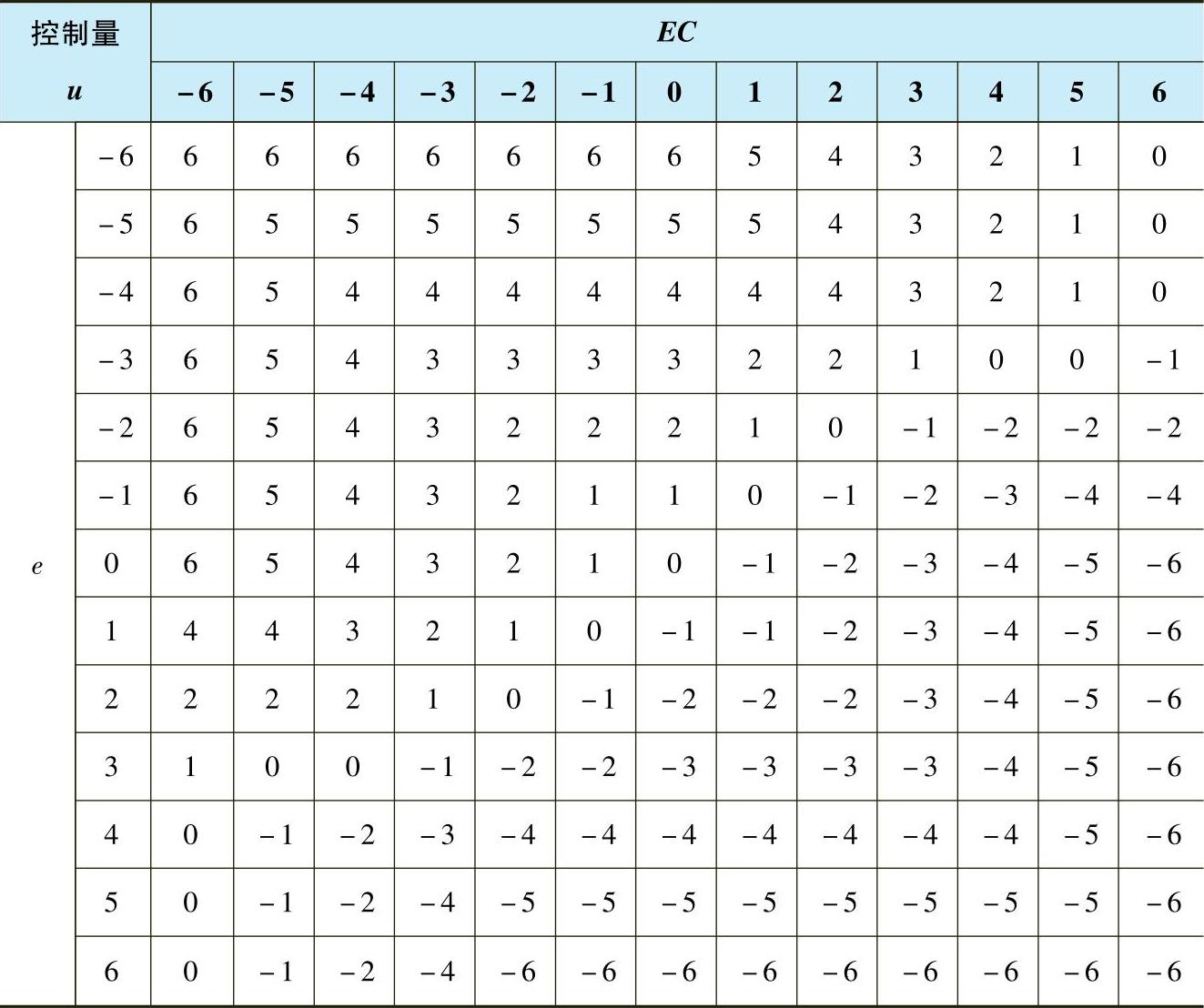
把49条控制规则输入MATLAB模糊逻辑工具箱的规则编辑器，用规则观察器可得出模糊控制表（见表7-3）。

表7-3 模糊控制表

从MATLAB模糊逻辑工具箱曲面观察器可观察到基于整个输入集（E、EC）变化区间的整个输出集（U）的变化范围，其表面形状如图7-9所示，从图中可以看出输入与输出之间呈现非线性关系，曲面的变化比较平缓，具有比较平滑的输出推理。

7.模糊控制实现

根据上述得到模糊控制表，将模糊控制表看成是二维的n×m矩阵表，其中n=m=13，将控制表的数据按行顺序存到计算机（工控机）或微控制器中，因此U_ij元素的位置为13i+j。在实际控制过程中，将采样电压信号作平均处理，然后进行偏差的计算和模糊控制表的查询，具体包括以下几步工作^[14]：

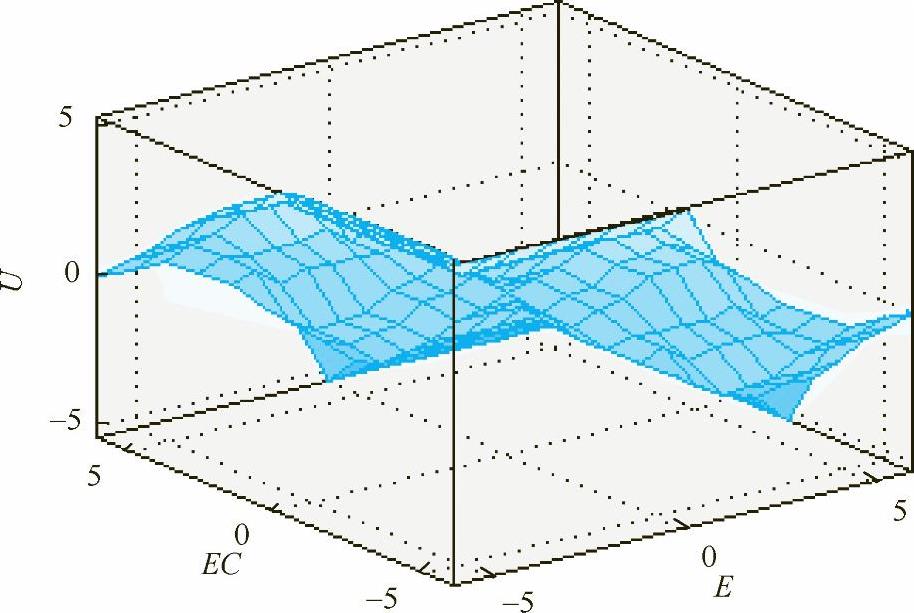
图7-9 模糊输入E、EC与输出U的关系

1）在每一个周期中采样电弧电压U_fn，并求取实际的即时偏差e_n和偏差变化率ec_n。

e=U_g-U_fn

ec=e_n-e_n-1 （7-28）

2）将实际的e和ec按下面公式计算

x=<k_ee+0.5>

y=<k_ecec+0.5> （7-29）

取得相应论域元素表征的查表所需要的x、y值。

3）以x、y分别按U_ij元素的位置为13i+j查找控制表的行和列，可得到控制量的论域值U_ij。

4）将查表得到的控制量的论域值U_ij和U_ij1按下面公式计算，即

u=k_uU_ij （7-30）

由此便可得到实际的控制量u，输出去调节送丝电动机的驱动电压，改变送丝速度v_f以实现电弧长度的实时控制。