如何优化BP神经网络？

1986年，Rumelhart等提出了Back Propagation Network，即BP神经网络，在目前有关神经网络的应用研究中，BP神经网络是广泛采用的算法之一^[5]。当训练数据充足的前提下，利用BP神经网络可以达到很好的预测效果。据统计，80%～90%的神经网络应用都采用了BP网络模型或者它的变形，有研究已经证明，在隐含层节点数目可以根据需要自由设置的情况下，三层前向BP网络可以实现以任何精度逼近任意连续函数^[6，7]。

BP神经网络是一种单向传播的多层前向网络，网络除输入输出结点外，还包括一层或多层隐含节点，同层内节点之间没有任何联系。输入信号从输入层节点依次传过各隐含层节点，然后传到输出节点，每一层节点的输出只影响到下一层节点的输出。基本BP算法主要包括两个过程：信号的前向传播以及误差的反向传播。即由输入通过BP网络计算实际输出是按前向进行，而修正权值和阈值的过程是按从输出到输入逆向进行。图6-1为标准的三层BP神经网络模型结构图。

下面以图6-1所示三层BP网络为例，介绍其学习过程。

首先对符号的形式及意义说明如下：

网络输入向量P_k=（a₁，a₂，...，a_n）；

图6-1 BP网络结构

网络目标向量T_k=（y₁，y₂，...，y_q）；

中间层单元输入向量S_k=（s₁，s₂，...，s_p），输出向量B_k=（b₁，b₂，...，bp）；

输出层单元输入向量L_k=（l₁，l₂，...，l_q）；输出向量C_k=（c₁，c₂，...，c_q）；

输入层至中间层的连接权w_ij，i=1，2，...，n，j=1，2，...，p；

中间层至输出层的连接权v_jt，j=1，2，...，p，t=1，2，...，q；

中间层各单元的输出阈值θ_j，j=1，2，...，p；

输出层各单元的输出阈值γ_t，t=1，2，...，q；

参数k=1，2，...，m，为训练样本序号。

BP神经网络学习过程及步骤如下：

1）初始化。给每个连接权值w_ij、v_jt、阈值θ_j、γ_t赋予区间（-1，1）内的随机值。

2）随机选取一组输入和目标样本P_k=（a^k₁，a₂^k，...，a^k_n）、T_k=（y^k₁，y^k₂，...，y^k_q）提供给网络。

3）中间层各节点的输入s_j可由输入样本P_k=（a^k₁，a₂^k，...，a^k_n）、连接权w_ij和阈值θ_j通过式（6-1）计算得出，中间层各节点的输出b_j可以用s_j通过传递函数求出。

b_j=f（s_j），j=1，2，...，p （6-5）

4）输出层各节点的输出L_t可以由中间层的输出b_j、权值v_jt和阈值γ_t计算得出，然后由传递函数即可计算输出层各节点的响应C_t。

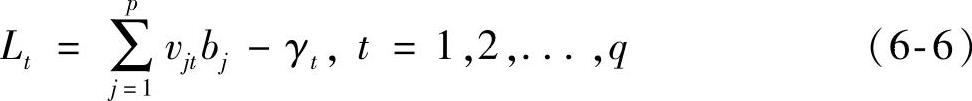
C_t=f（L_t），t=1，2，...，q （6-7）

5）输出层的各节点一般化误差d^k_t可以通过目标向量T_k=（y^k₁，y^k₂，...，y^kq）和网络实际输出C_t由式（6-8）计算得出。

d^k_t=（y^k_t-C_t）·C_t·（1-C_t），t=1，2，...，q （6-8）

6）中间层各节点的一般化误差e_j^k可以通过连接权值v_jt、输出层各节点一般化误差d^k_t和中间层的输出b_j由式（6-9）计算得出。(www.xing528.com)

7）连接权值v_jt和阈值γ_t的修正可以利用输出层各节点的一般化误差d^k_t与中间层各节点的输出b_j通过式（6-10）和式（6-11）实现。

v_jt（N+1）=v_jt（N）+α·d^k_t·b_j （6-10）

γ_t（N+1）=γ_t（N）+α·d^k_t （6-11）

t=1，2，...，q，j=1，2，...，p，0＜α＜1

8）连接权w_ij和阈值θ_j的修正可以利用中间层各节点的一般化误差e_j^k和输入层各节点的输入P_k=（a^k₁，a₂^k，...，a^k_n）通过式（6-12）和式（6-13）实现。

w_ij（N+1）=w_ij（N）+βe_j^ka^k_i （6-12）

θ_j（N+1）=θ_j（N）+βe_j^k （6-13）

i=1，2，...，n，j=1，2，...，p，0＜β＜1

9）接着继续随机选取一个学习样本提供给BP网络，从步骤3）开始重复以上过程，直到m个训练样本训练完毕为止。

10）随机地从m组学习样本中选取一组输入向量和目标向量，返回步骤3）重复迭代过程，直到网络收敛为止，即全局误差E小于设定的某一阈值。如果全局误差始终大于预先设定的值，表明网络无法收敛。

11）网络学习结束。

从以上步骤可以看出，第7）～8）步为网络误差的反向传播过程，第9）～10）步为完成网络训练的过程。

虽然标准的BP神经网络具有结构简单，泛化能力强，容错性好等优点，但由于存在收敛速度慢和目标函数存在局部极小的问题，使得实际应用中BP神经网络运算速度慢、预测精度低。因此，需要对其进行改进以取得更快的网络收敛速度和更好的预测结果。目前常用的BP网络改进措施有动量法、自适应调整学习率法以及L-M优化方法等。

1）动量法。标准BP算法只按照t时刻负梯度方向来修正权值W（t+1），并没有考虑过往时刻的梯度方向，因而会导致训练过程中产生振荡，使收敛速度缓慢。动量因子的加入可以使网络对误差曲面局部调节的敏感性降低，这样就降低了网络陷入局部极小的概率。动量法中网络学习的校正量受到前一次学习校正量的影响，因而可以加快网络的收敛速度。即

ΔW′（N）=ΔW（N）+GΔW（N-1） （6-14）

式中 G——动量因子，0＜G＜1。

2）自适应调整学习率法。在自适应调整学习率法中，网络学习速率随误差曲面的梯度改变而改变，能有效提高网络的收敛速度。其基本思想是：首先检查权值阈值的修正是否真正降低了误差；若误差降低，说明学习效率较低，可以对其适当增加一个量，反之，则说明已经过调，应适当减小网络的学习速率。具体调整公式为

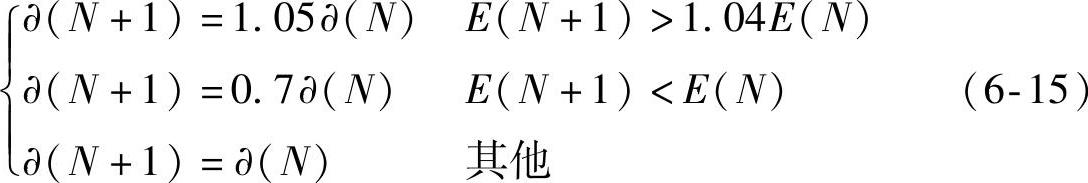
3）L-M优化方法。L-M优化方法的权值调整策略为

ΔW=（J^TJ+UJ）^-1J^TE （6-16）

式中 J——误差对权值微分的雅可比矩阵；

E——误差向量；

U——能自适应调整的学习速率。

L-M优化方法将梯度下降法和拟牛顿法各自的优势相结合，充分利用梯度下降法在开始阶段收敛速度快的特点和拟牛顿法在极值附近能很快产生一个理想搜索方向的特点，使得网络的收敛速度和准确率均有所提高。