经验模式分解（EMD）方法和与之相应的Hilbert谱统称为Hilbert-Huang变换。由第4章内容介绍可知道，EMD方法可以将信号分解为若干个内模式分量IMF分量之和及一个剩余分量rn，见式（5-10），该剩余分量是一个平均趋势或者是一个常数。
忽略剩余分量rn，对式（5-10）中的每个内禀模态函数ci（t）做Hilbert变换得到
忽略剩余分量rn，对式（5-10）中的每个内禀模态函数ci（t）做Hilbert变换得到
构造解析信号为
构造解析信号为
于是得到幅值函数和相位函数分别为式（5-13）和式（5-14）
于是得到幅值函数和相位函数分别为式（5-13）和式（5-14）
进一步可以求出瞬时频率为
进一步可以求出瞬时频率为
这样，可以得到(www.xing528.com)
这样，可以得到
其中RP表示取实部。展开式（5-16）称为Hilbert谱，记作
其中RP表示取实部。展开式（5-16）称为Hilbert谱，记作
式（5-17）精确地描述了信号的幅值在整个频率段上随时间和频率的变化规律。信号幅度在三维空间表示为时间和瞬时频率的函数，信号幅度也可以表示成时间频率平面的等高线。
式（5-17）精确地描述了信号的幅值在整个频率段上随时间和频率的变化规律。信号幅度在三维空间表示为时间和瞬时频率的函数，信号幅度也可以表示成时间频率平面的等高线。
将信息熵引入时频分析的思路和进行时频熵计算的方法是将时频平面等分为N个面积相等的时频块，每块内的能量为Wi（i=1，2，…，N），整个时频平面的能量为A，对每区块进行能量归一化，得qi=Wi/A，于是有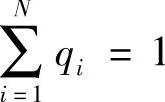
，符合计算信息熵的初始归一化条件。仿照信息熵的计算公式，基于Hilbert-Huang变换的时频熵计算公式为
将信息熵引入时频分析的思路和进行时频熵计算的方法是将时频平面等分为N个面积相等的时频块，每块内的能量为Wi（i=1，2，…，N），整个时频平面的能量为A，对每区块进行能量归一化，得qi=Wi/A，于是有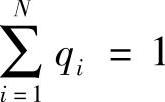
，符合计算信息熵的初始归一化条件。仿照信息熵的计算公式，基于Hilbert-Huang变换的时频熵计算公式为
根据信息熵的基本性质，qi分布越均匀，时频熵值s（q）越小，反之时频熵值s（q）越大。
根据信息熵的基本性质，qi分布越均匀，时频熵值s（q）越小，反之时频熵值s（q）越大。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
