应用实例：小波能谱熵计算中的采样和波形处理分析

1.不同频率下电弧电流信号的计算与分析

采用MZE1000交流方波埋弧焊机，进行埋弧焊接平铺试验，工件材料为低碳钢，板厚20mm，焊丝牌号为H08A，直径4.0mm，焊剂HJ431。分别改变焊接参数，利用基于霍尔效应的电流传感器和基于以太网的高速数据采集卡进行电流信号采集。采样频率为25kHz，每个焊接过程采样20s，从中截取5s即125000个数据点来进行小波能谱熵的计算。

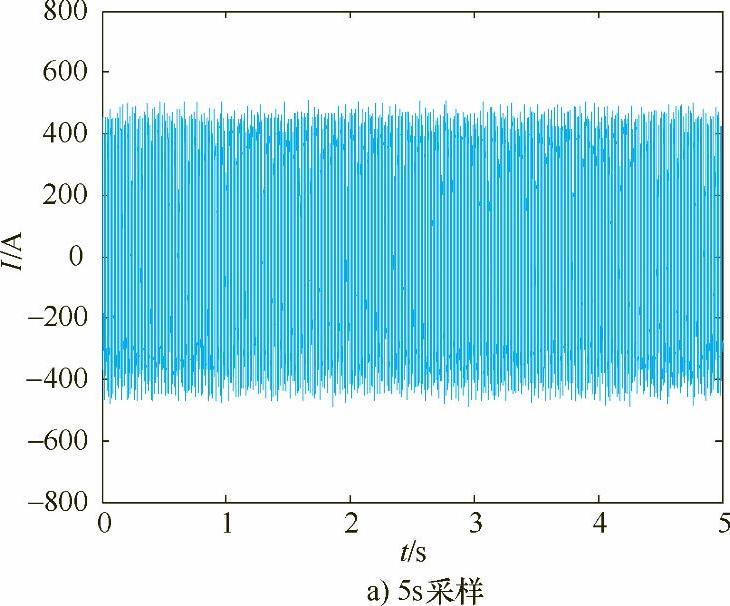
图5-1 50Hz的电流波形

图5-1～图5-4给出了在给定电压为40V、电流正负幅400A，焊丝伸出长度为20mm，焊接速度1.0m/min的条件下，不同焊接电流波形频率的焊接电弧电流波形。其中图a为采样时间为5s的波形，图b为相应波形的0.1s局部放大效果。

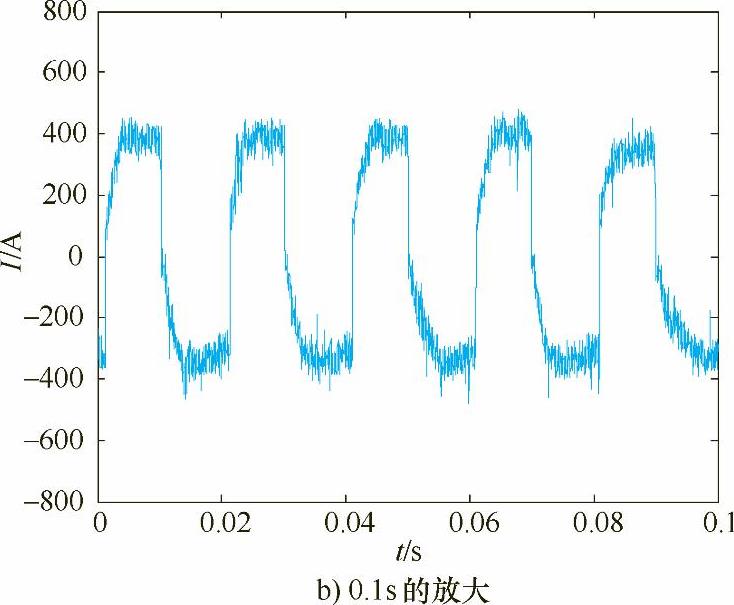
图5-1 50Hz的电流波形（续）

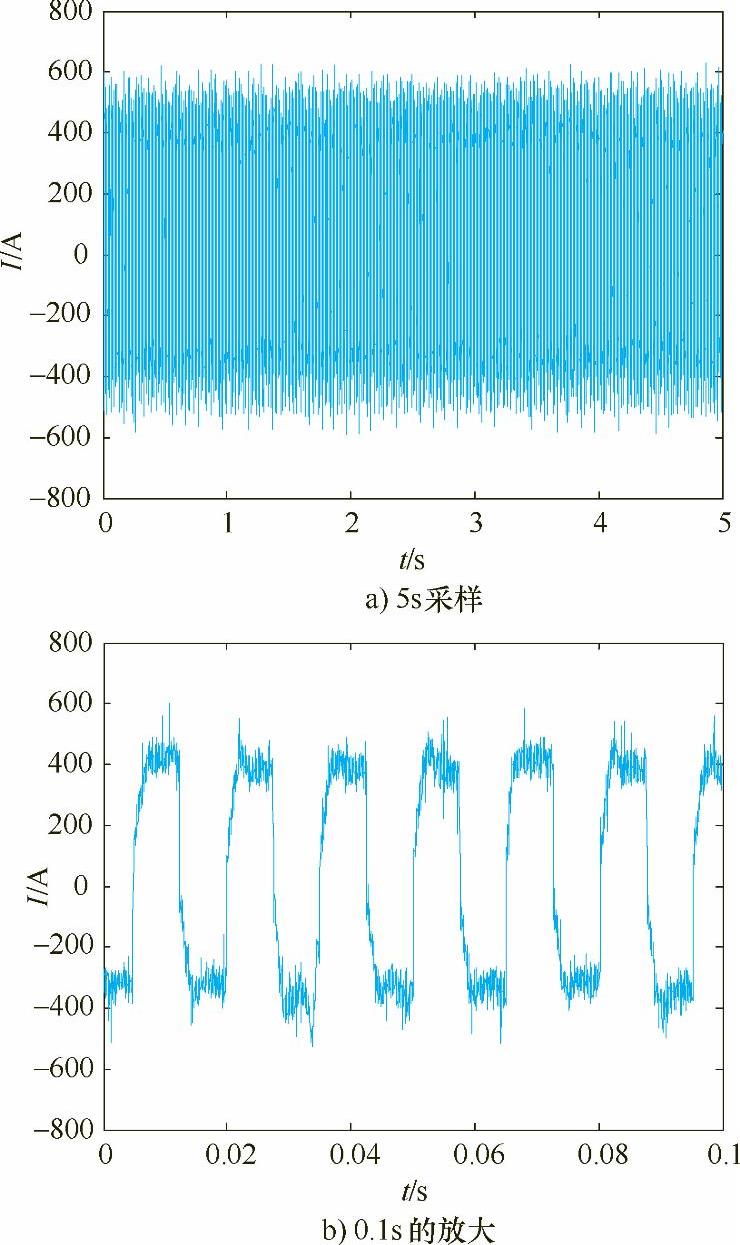
图5-2 80Hz的电流波形

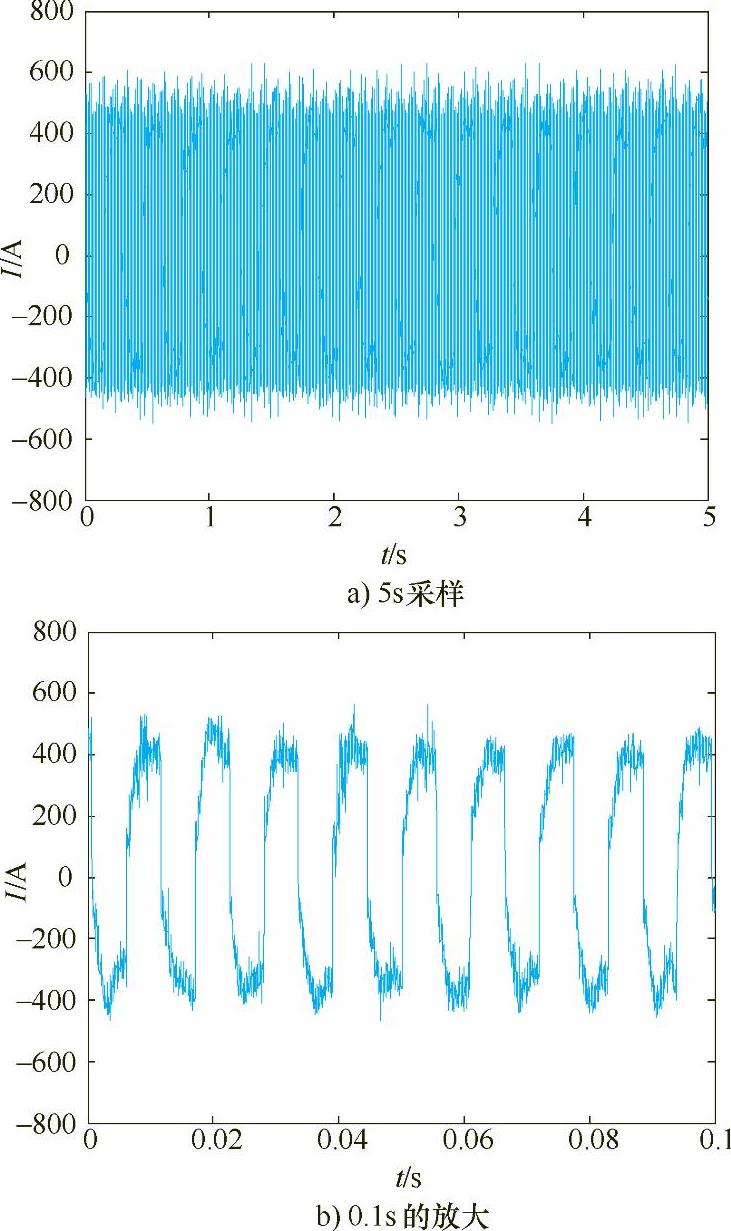
图5-3 100Hz的电流波形

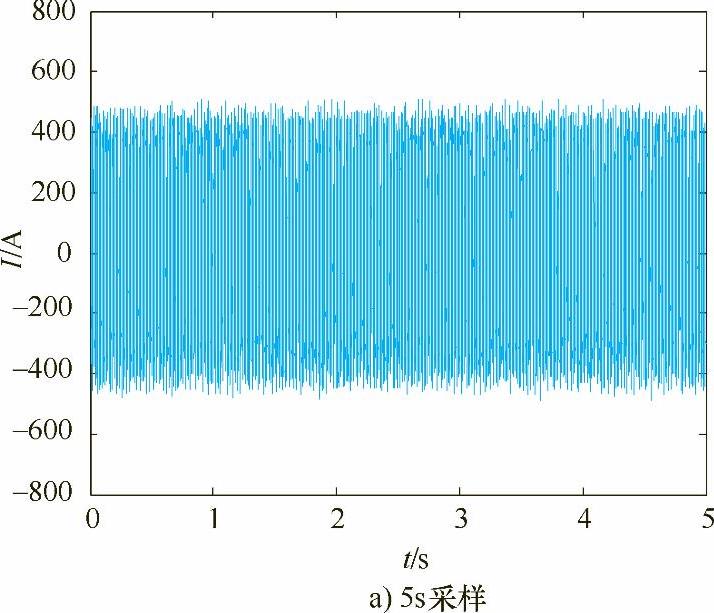
图5-4 120Hz的电流波形

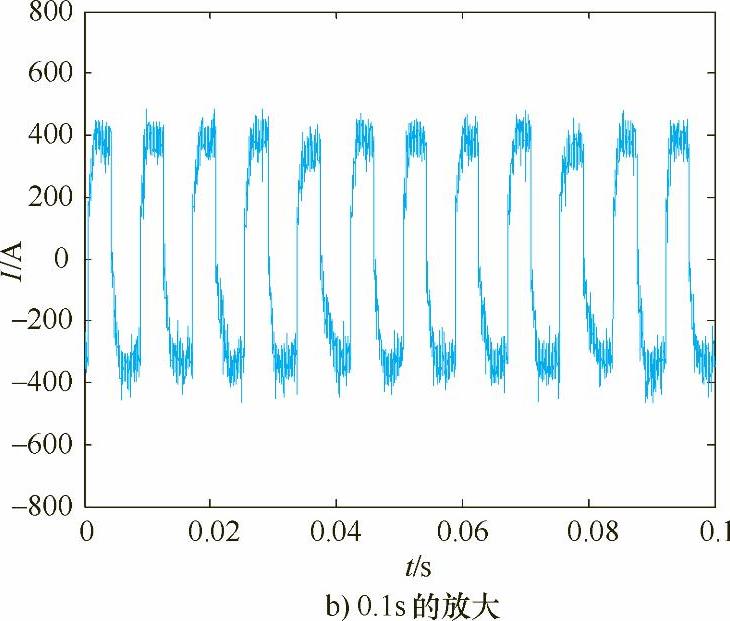
图5-4 120Hz的电流波形（续）

选取一滑动时窗，窗长L=1000，滑动步长δ=1，对以上四组不同频率下的焊接电流采样信号进行小波能谱熵分析，绘出各自小波能谱熵随时间的变化曲线分别如图5-5、图5-6所示，然后计算不同频率下所得电流信号小波能谱熵的均值，结果见表5-1。

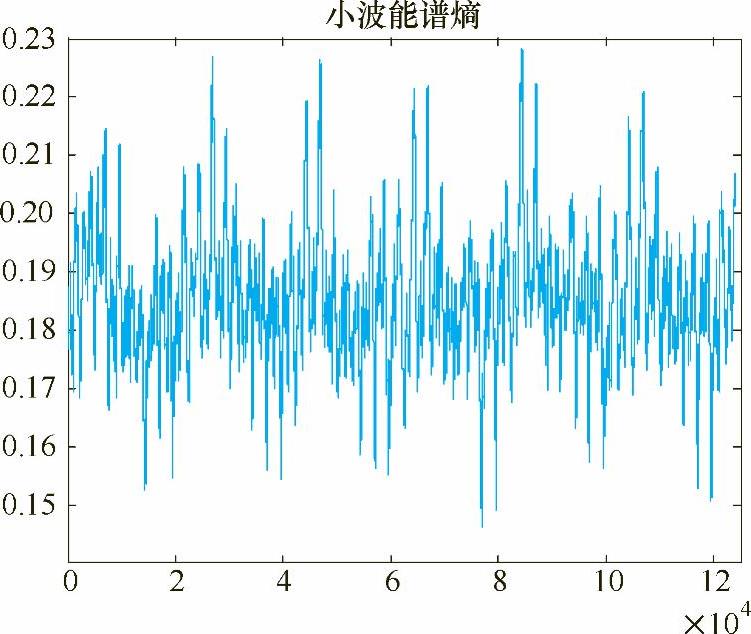
图5-5 50Hz和80Hz电流信号的小波能谱熵

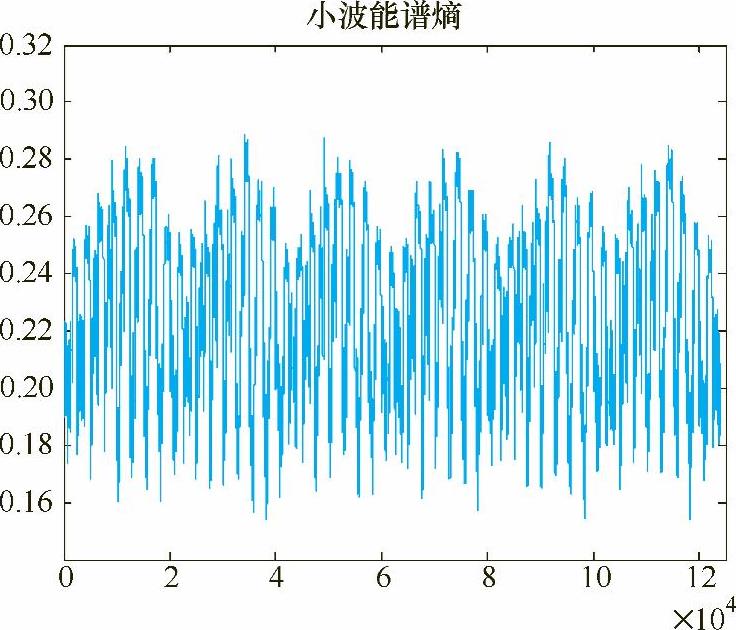
图5-5 50Hz和80Hz电流信号的小波能谱熵（续）

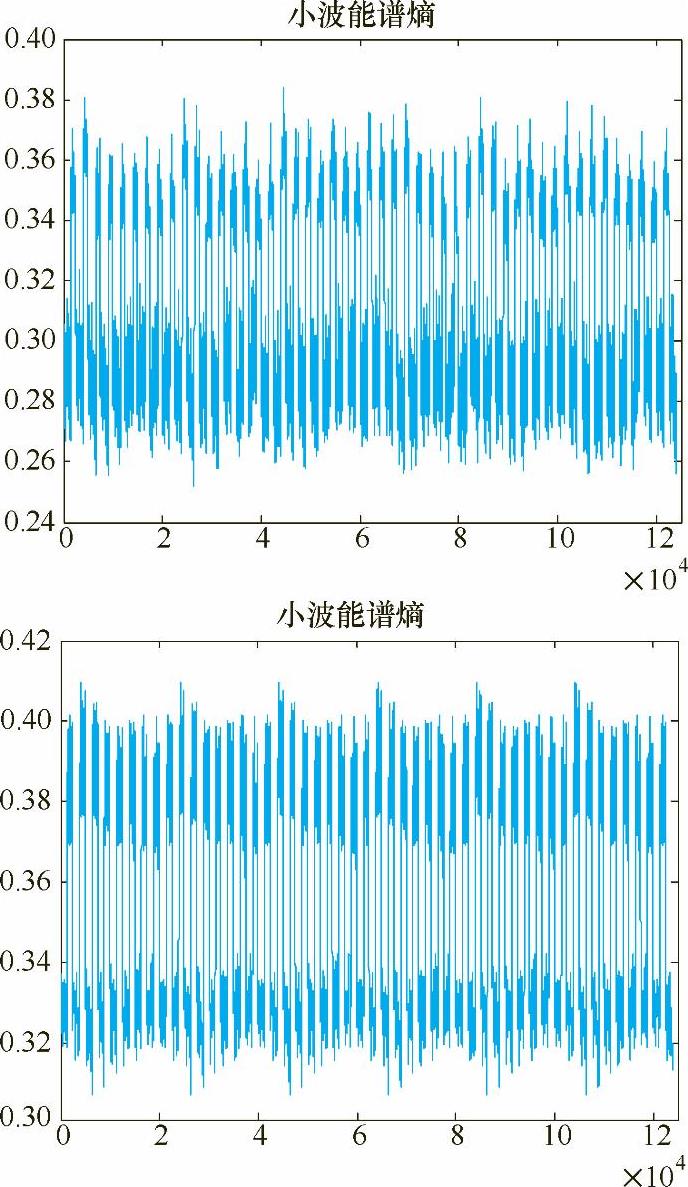
图5-6 100Hz和120Hz电流信号的小波能谱熵

表5-1 不同频率下的焊接参数及电流信号的小波能谱熵均值

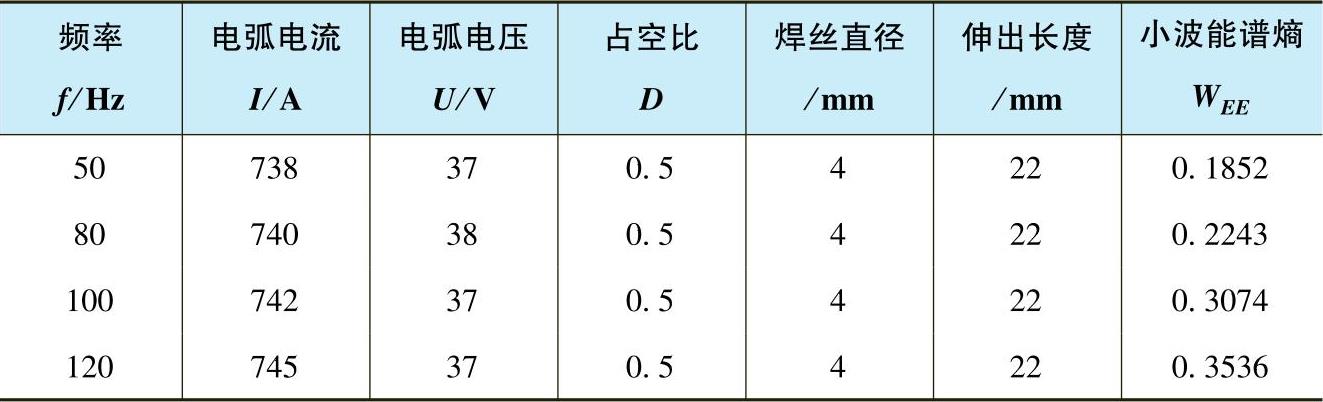
比较图5-1～图5-4可知，随着电流频率的增加，焊接过程的稳定性变得更好，电流信号变得更加规则，焊接过程无短路、无断弧、焊接过程稳定、焊缝成形好。由图5-5、图5-6不同频率下电流信号的小波能谱熵波形可以看出，随着频率的不断增大，小波能谱熵的波动越来越规则，说明随着频率的增加，电流信号变得更加稳定。随着频率的不断增加，小波能谱熵的均值不断增大，这是由小波能谱熵的性质决定的，因为频率越高，信号的熵值就会越大，但这并不影响其对信号稳定性的评估。因此，在相同占空比、不同电流波形频率下，小波能谱熵可以作为一种交流方波埋弧焊电弧稳定性的判据。

2.不同占空比下的电流信号计算与分析

在给定电压为40V、电流正负幅400A，焊丝伸出长度为20mm，焊接速度为1.0m/min基本保持不变的条件下逐渐增加焊接电流波形占空比的焊接电弧电流波形如图5-7～图5-13所示，从图中可见这些焊接过程基本上都是处于稳定状态。

选取一窗长为L=1000的滑动时窗，滑动步长为δ=1，对以上七组不同占空比下的焊接电流采样信号进行小波能谱熵分析，绘出各自小波能谱熵随时间的变化曲线分别如图5-14～图5-17所示，然后计算不同频率下所得电流信号小波能谱熵的均值，结果见表5-2。

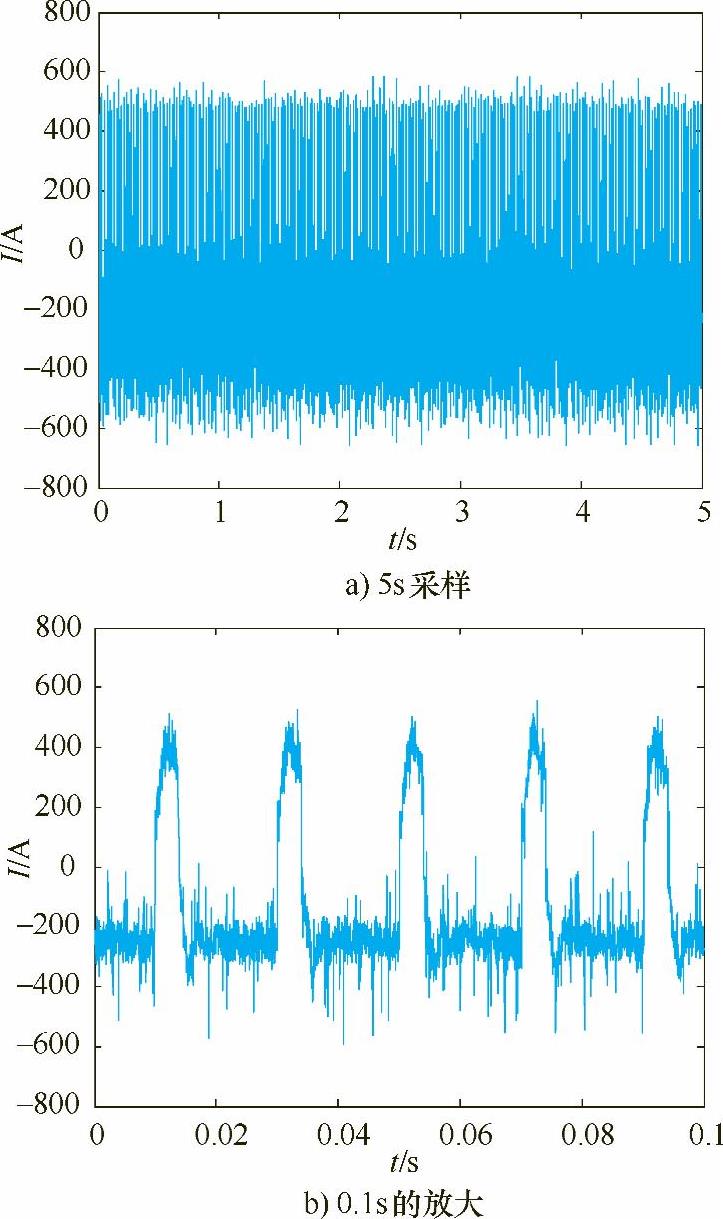
图5-7 占空比为0.2采集的电流信号

(www.xing528.com)

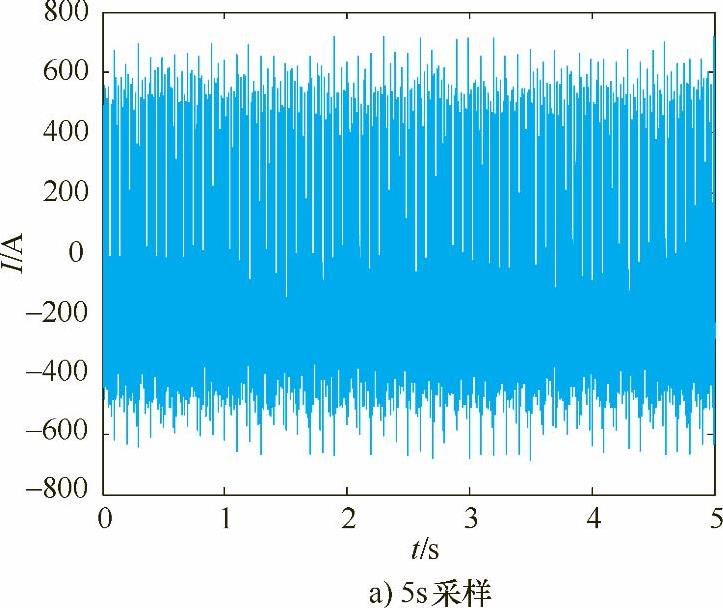
图5-8 占空比为0.3采集的电流信号

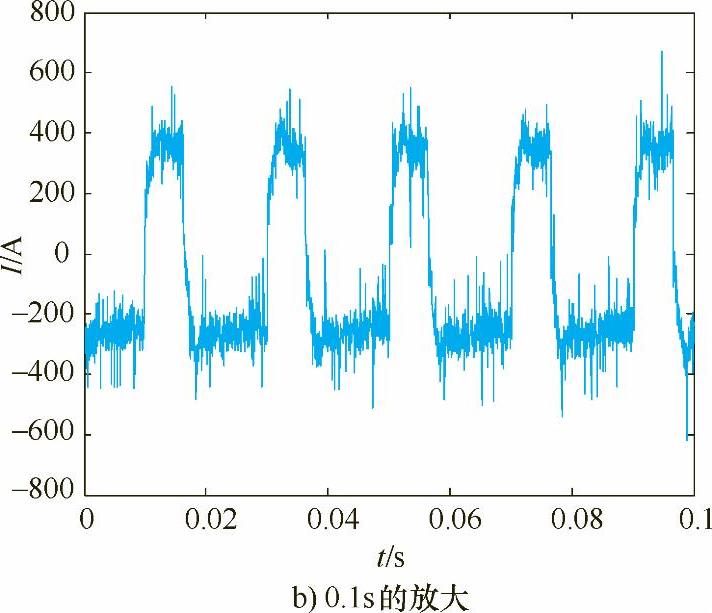
图5-8 占空比为0.3采集的电流信号（续）

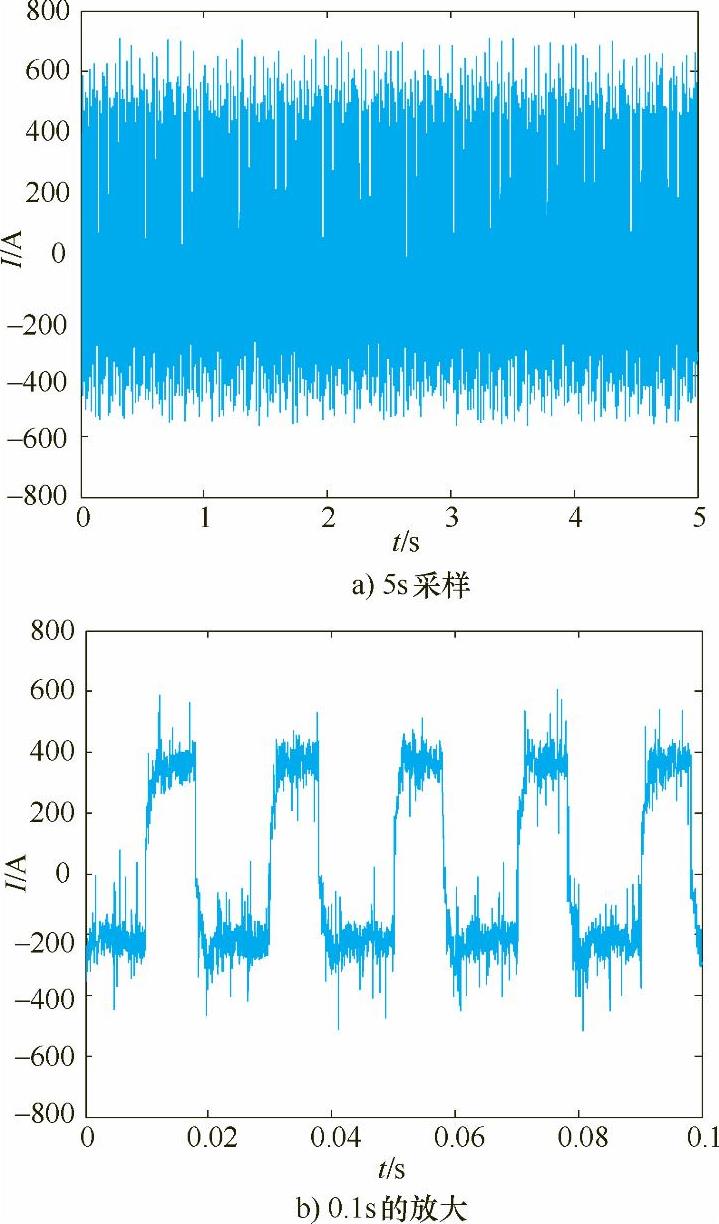
图5-9 占空比为0.4采集的电流信号

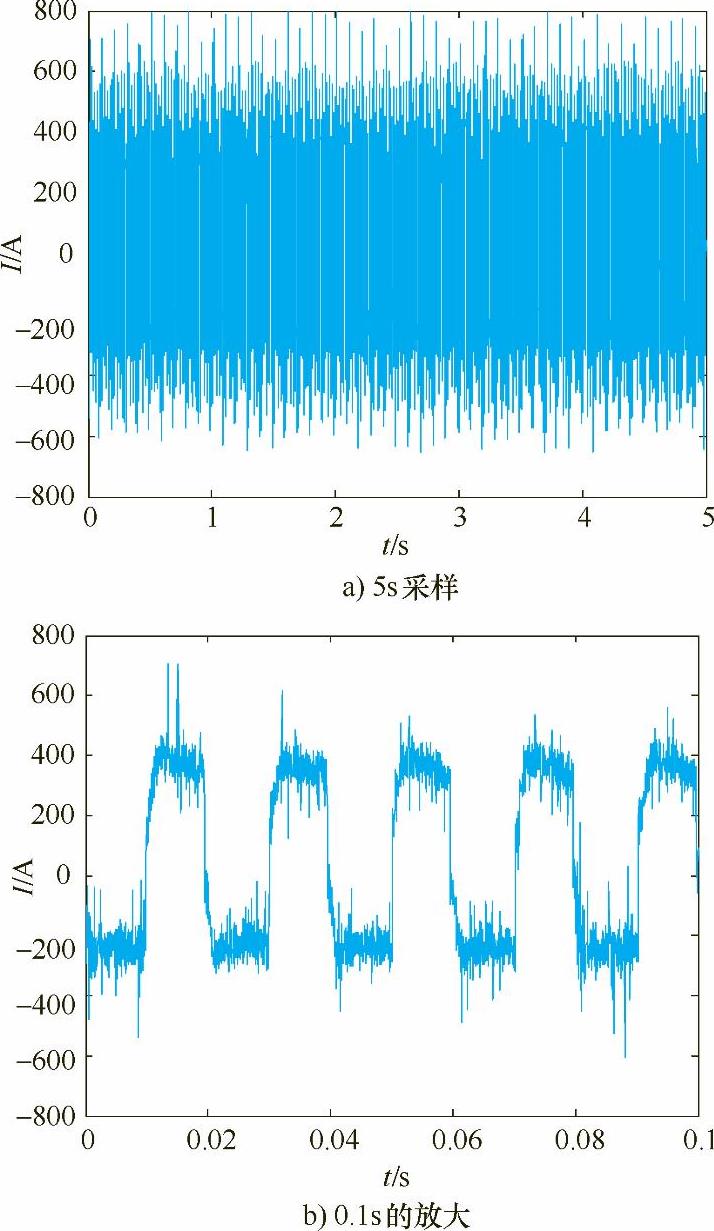
图5-10 占空比为0.5采集的电流信号

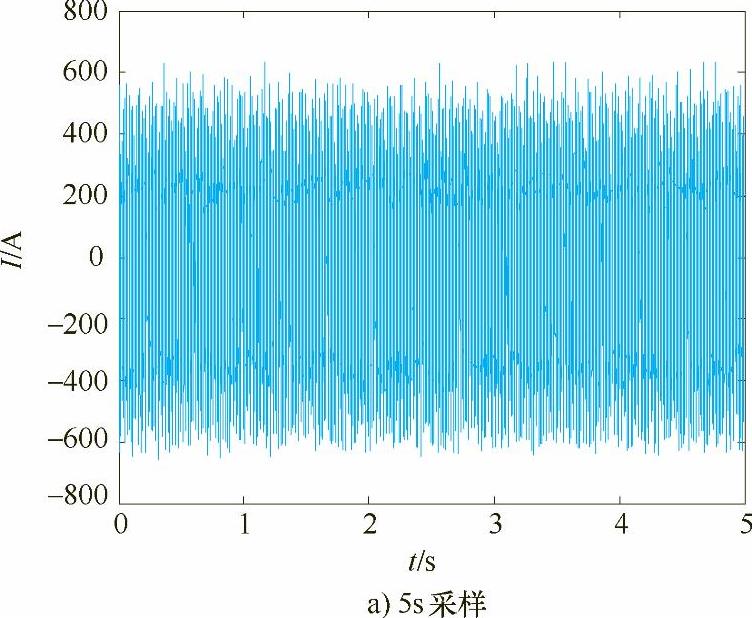
图5-11 占空比为0.6采集的电流信号

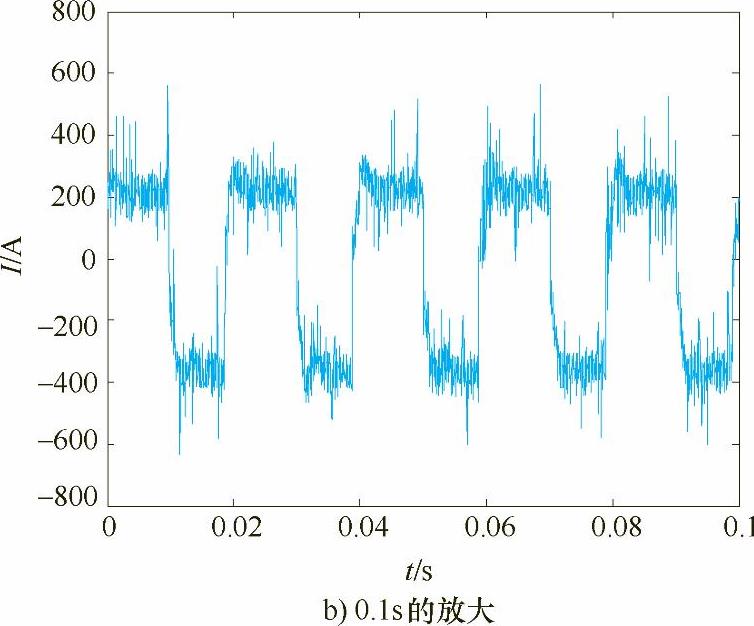
图5-11 占空比为0.6采集的电流信号（续）

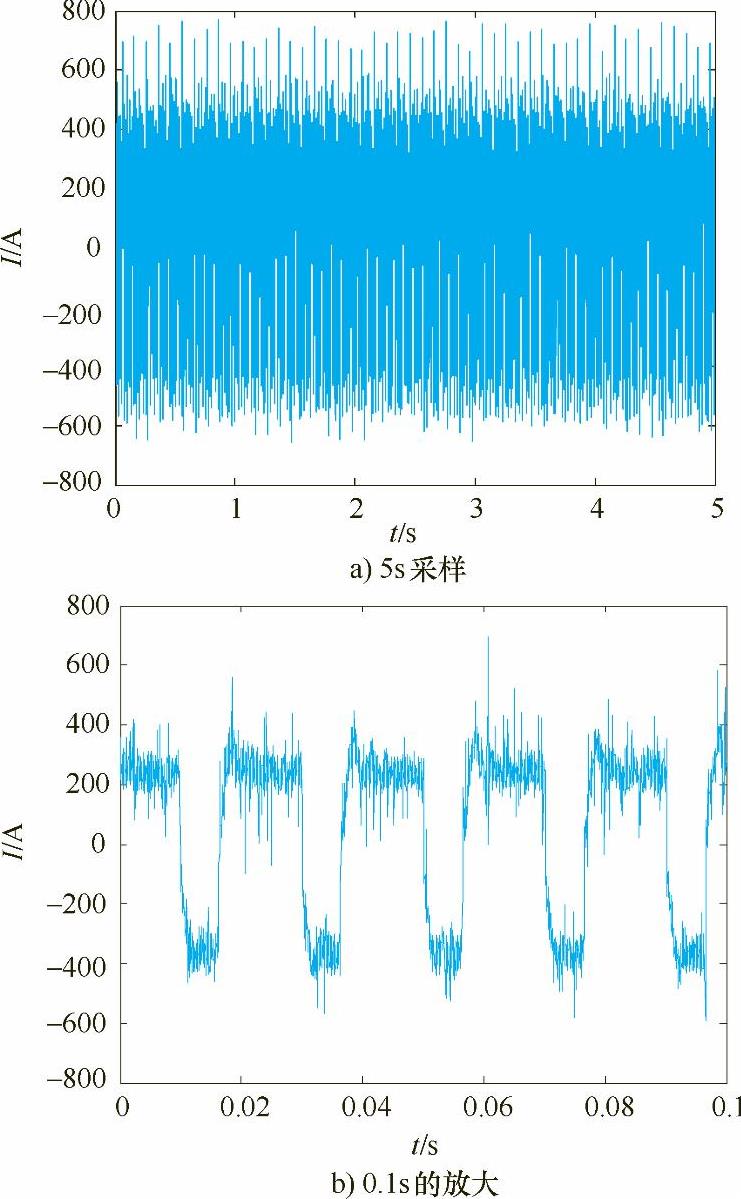
图5-12 占空比为0.7采集的电流信号

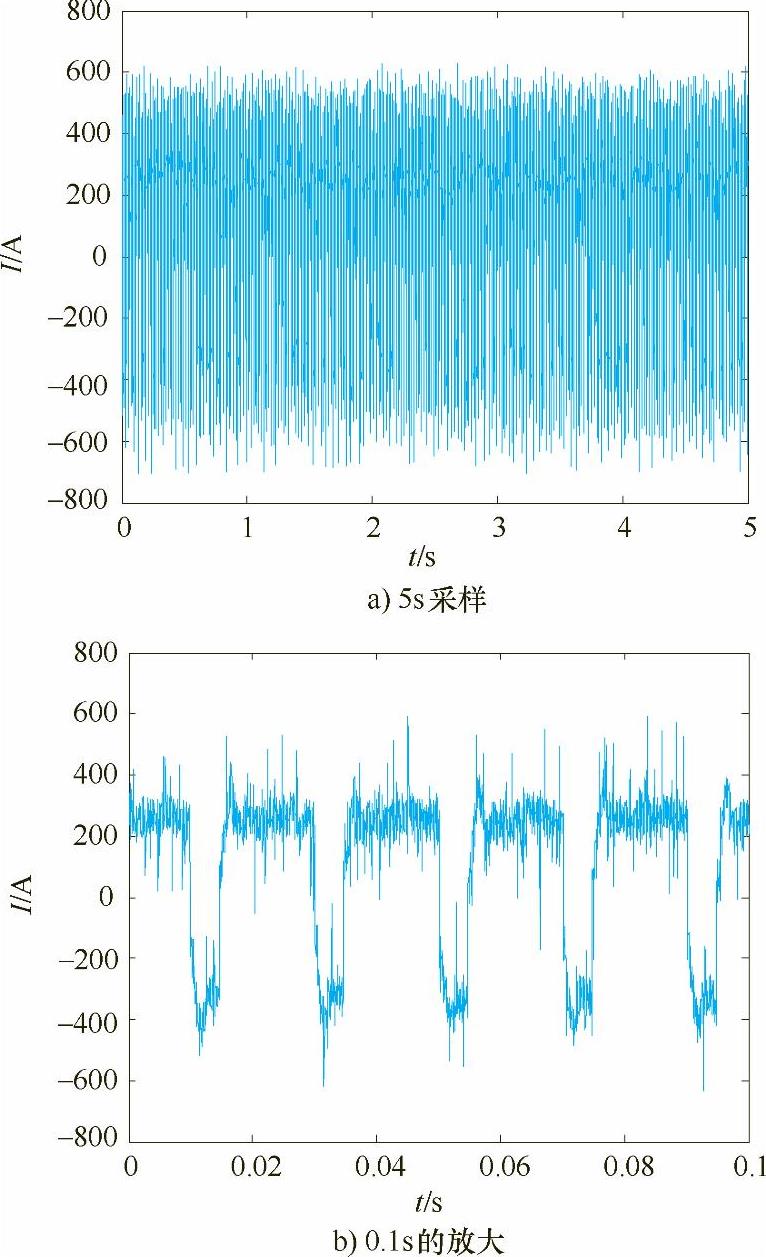
图5-13 占空比为0.8采集的电流信号

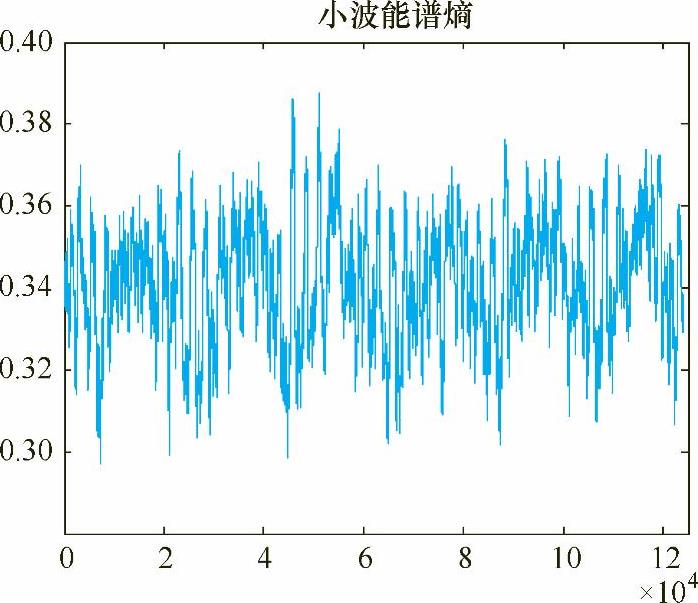
图5-14 占空比为0.2和0.3时电流信号的小波能谱熵

图5-14 占空比为0.2和0.3时电流信号的小波能谱熵（续）

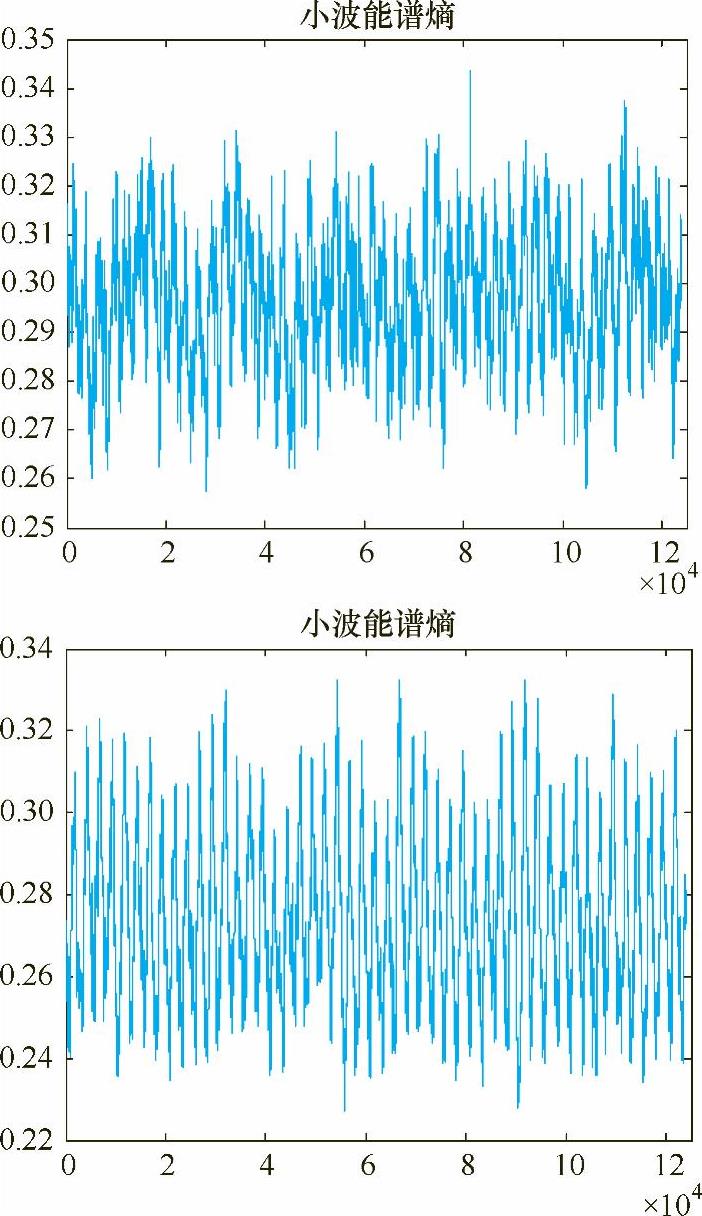
图5-15 占空比为0.4和0.5时电流信号的小波能谱熵

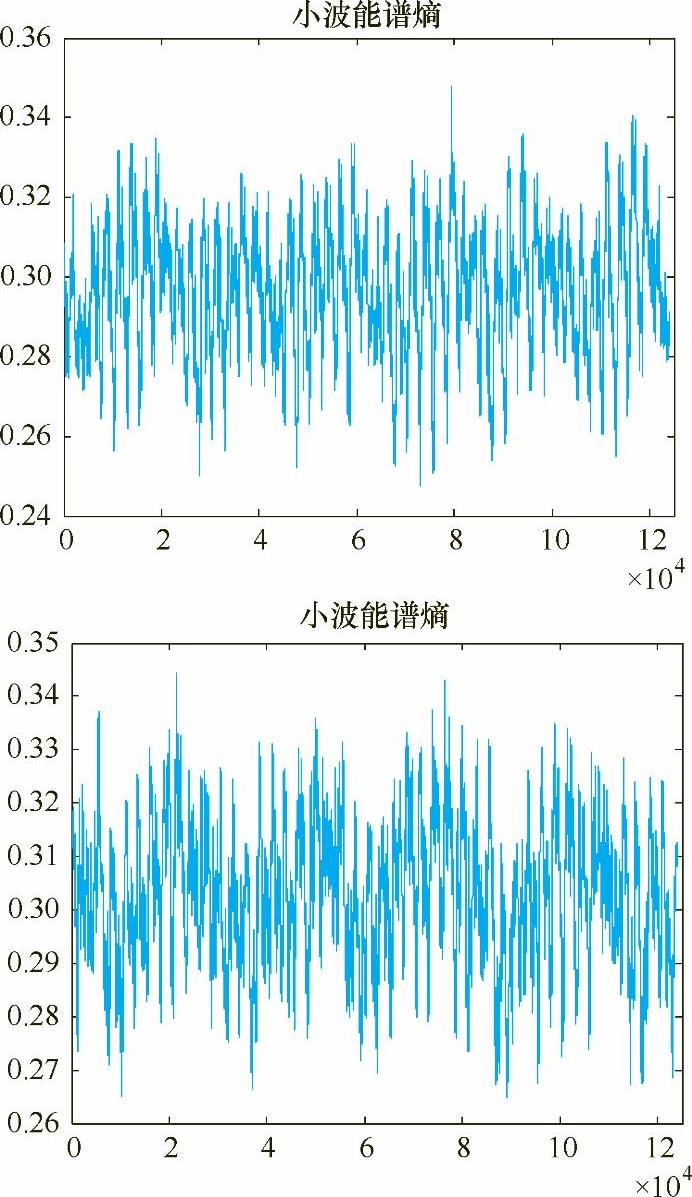
图5-16 占空比为0.6和0.7时电流信号的小波能谱熵

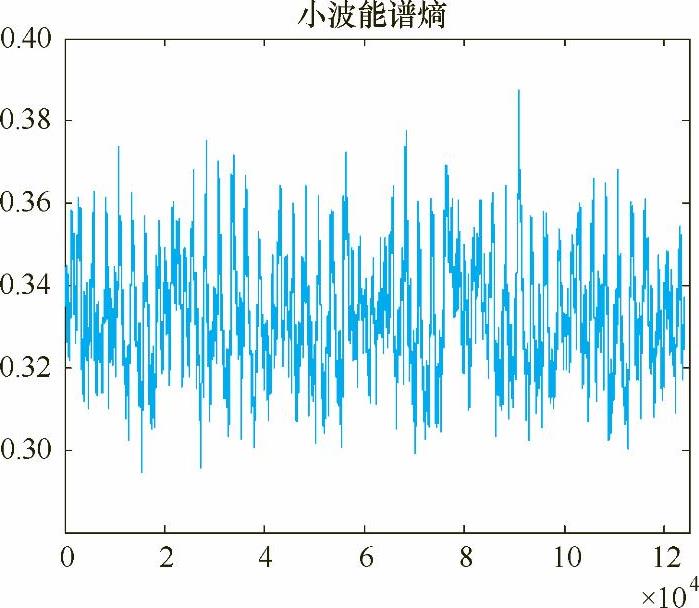
图5-17 占空比为0.8时电流信号的小波能谱熵

表5-2 不同占空比下的焊接参数及电流信号小波能谱熵计算结果

表5-2给出了电流波形在相同频率50Hz下不同占空比下焊接参数与小波能谱熵均值的计算结果，其中电弧电流、电压是指实际采集的焊接电流、电压信号的正负半波幅-幅值的平均值。比较图5-7a～图5-13a，发现焊接过程较为稳定，电流波动较小的为图5-9、图5-10和图5-11，即占空比为0.4、0.5和0.6。这是由于在相同焊接电流、电压、频率和焊接速度焊接时，占空比较小时，负半波电弧作用时间长，对焊丝熔化作用较大，而电弧正半波作用时间较短，从而使得焊丝熔滴处于大熔滴渣壁过渡状态，焊接过程不稳定。随着占空比的增大，电弧正半波电弧力作用增大，负半波电弧作用时间变小，焊丝熔滴由大变小并由渣壁过渡，电流波动变小，焊接过程稳定。在试验中，当占空比达到0.7时，由于正半波电弧作用时间增大，负半波电弧作用时间减少，从而使得焊丝熔滴在长大过程中伴随部分熔滴由渣壁过渡，这时电弧挺度较小，电流波动变大。只有在电流波形正负半波作用时间匹配时，焊丝熔化与过渡达到一种平衡，焊接过程最为稳定，电流波动最小，所以占空比为0.4～0.6是在此给定电压下的最佳焊接参数。由表5-2可知，占空比为0.4、0.5和0.6的小波能谱熵也最小。

由表5-2可知，在占空比由小到大逐渐增加时，小波能谱熵是逐渐减小的，直到占空比为0.5时达到最小值。小波能谱熵是一个复杂性的度量，所以当电流波形越规则时小波能谱熵应该越小。同时发现在占空比超过0.5后，小波能谱熵又开始逐渐增大。这表明交流方波埋弧焊过程电流波形占空比是影响信号小波能谱熵的一个因素，与焊接过程的稳定性有着密切的联系。焊接过程越稳定小波能谱熵越小。实际上，在较低占空比时，占空比由小到大的增加，是稳定性增加的一个表征，因为此时是由不稳定的大熔滴渣壁过渡状态逐渐转变为稳定的熔滴渣壁过渡的过程。因此在给定焊接电流、电压时，不同电流波形占空比下，小波能谱熵能作为交流方波埋弧焊过程稳定性的评判标准。